Паралле́льные прямы́е (от греч. παράλληλος, буквально — идущий рядом) — в планиметрии прямые, которые не пересекаются, сколько бы их ни продолжали в обе стороны.
Содержание
В евклидовой геометрии
На чертежах параллельные линии выделяются одинаково направленными стрелками.
В евклидовой геометрии параллельными прямыми называются прямые, которые лежат в одной плоскости и не пересекаются[1].В другом варианте определения совпадающие прямые также считаются параллельными[2][3].
Преимущество последнего определения состоит в том, что параллельность становится отношением эквивалентности[4].
Параллельность прямых m{displaystyle m}
и n{displaystyle n} обычно обозначается:
и n{displaystyle n}
обычно обозначается: m∥n{displaystyle mparallel n}
Свойства
- Через любую точку, не лежащую на прямой, можно провести прямую, параллельную данной, и притом только одну. Последняя часть этого утверждения — знаменитый пятый постулат Евклида. Отказ от пятого постулата ведёт к геометрии Лобачевского (см. ниже).
- Если прямая пересекает одну из параллельных прямых, то она пересекает и другую (такая прямая называется секущей). При этом образуется 8 углов, некоторые характерные пары которых имеют особые названия и свойства:
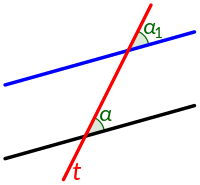
- Соответственные углы равны (Рис.1).
- Накрест лежащие углы равны (Рис.2).
- Внутренние односторонние углы в сумме составляют 180° (Рис.3).
 |
 |
 |
| Рис.1: Соответственные углы равны, α=α1{displaystyle alpha =alpha _{1}} . | Рис.2: Внутренние накрест лежащие углы равны, α=γ1{displaystyle alpha =gamma _{1}} . | Рис.3: Односторонние углы являются дополнительными, α+δ1=180∘{displaystyle alpha +delta _{1}=180^{circ }} . |
.
.
.- Если считать совпадающие прямые параллельными, то параллельность будет бинарным отношением эквивалентности, которое разбивает всё множество прямых на классы параллельных между собой прямых.
- Множество точек плоскости, расположенных на некотором фиксированном расстоянии от данной прямой, по одну сторону от неё, есть прямая, параллельная данной.
Построение параллельных прямых
В стереометрии
В планиметрии две различные прямые либо пересекаются, либо параллельны. В стереометрии возможен третий вариант — прямые могут не пересекаться, так как не лежат в одной плоскости. Такие прямые называются скрещивающимися.
В геометрии Лобачевского
Параллельные прямые в модели Пуанкаре: две зелёные прямые равнобежны (асимптотически параллельны) синей прямой, а фиолетовая ультрапараллельна к ней
В геометрии Лобачевского в плоскости через точку C{displaystyle C}
вне данной прямой AB{displaystyle AB} проходит бесконечное множество прямых, не пересекающих AB{displaystyle AB} .Прямая CE{displaystyle CE} называется равнобежной прямой AB{displaystyle AB} в направлении от A{displaystyle A} к B{displaystyle B} , если:
вне данной прямой AB{displaystyle AB}
проходит бесконечное множество прямых, не пересекающих AB{displaystyle AB}
называется равнобежной прямой AB{displaystyle AB}
к B{displaystyle B}
, если:- точки B{displaystyle B} и E{displaystyle E} лежат по одну сторону от прямой AC{displaystyle AC} ;
- прямая CE{displaystyle CE} не пересекает прямую AB{displaystyle AB} , но всякий луч, проходящий внутри угла ACE{displaystyle ACE} , пересекает луч AB{displaystyle AB} .
лежат по одну сторону от прямой AC{displaystyle AC}
;
, пересекает луч AB{displaystyle AB}Аналогично определяется прямая, равнобежная AB{displaystyle AB}
в направлении от B{displaystyle B} к A{displaystyle A} .
Равнобежные прямые называются также асимптотически параллельными или просто параллельными.Все остальные прямые, не пересекающие данную, называются ультрапараллельными или расходящимися[5].
Свойства
Расходящиеся параллельные прямые имеют единственный общий перпендикуляр.Этот перпендикуляр соединяет ближайшую пару точек на этих прямых.
Несмотря на то, что асимптотически параллельные прямые не пересекаются, на любой паре асимптотически параллельных прямых можно выбрать произвольно близкие точки.
См. также
Примечания
- ↑ Параллельные прямые // Большая советская энциклопедия : [в 30 т.] / гл. ред. А. М. Прохоров. — 3-е изд. — М. : Советская энциклопедия, 1969—1978.
- ↑ Земляков А. Н. Аксиоматический подход к геометрии (тезисы) // Математическое образование. — 2001. — № 3(18). — С. 4-21.
- ↑ Адамар Ж. Элементарная геометрия. — М., 1948. — С. 52.
- ↑ Шиханович Ю. А. Введение в современную математику (Начальные понятия). — М.: Наука, 1965. — С. 259. — 376 с.
- ↑ Математический справочник
| Это статья-заготовка по геометрии. Помогите Википедии, дополнив эту статью, как и любую другую. |
