Парадокс близнецов

Разделы:

Парадо́кс близнецо́в — мысленный эксперимент, при помощи которого пытаются «доказать» противоречивостьспециальной теории относительности.Согласно СТО, с точки зрения «неподвижных» наблюдателей все процессы у двигающихся объектов замедляются.С другой стороны, принцип относительности декларирует равноправиеинерциальных систем отсчёта.На основании этого строится рассуждение, приводящее к кажущемуся противоречию.Для наглядности рассматривается история двух братьев-близнецов. Один из них (далее путешественник) отправляется в космический полёт, второй (далее домосед) — остаётся на Земле. После полёта путешественник совершает возврат на Землю.Чаще всего «парадокс» формулируется следующим образом:

Формулировка I.С точки зрения домоседа часы движущегося путешественника имеютзамедленный ход времени, поэтому при возвращении они должны отстать от часов домоседа.С другой стороны, в системе отсчета путешественника двигалась и ускорялась Земля, поэтому отстать должны часы домоседа.На самом деле братья равноправны, следовательно, после возвращения их часы должны показывать одно время.

Тем не менее, согласно СТО,отставшими окажутся часы путешественника. В таком нарушении видимой симметричности братьев и усматривается противоречие.

Содержание

1 История
2 Классификация объяснений парадокса
3 Кинематические эффекты СТО
- 3.1 Замедление времени
- 3.2 Относительность одновременности
4 Простейшие объяснения
5 Физическая причина парадокса
6 Обмен сигналами
- 6.1 Расчёт путешественника
- 6.2 Расчёт домоседа
7 Геометрическая интерпретация
8 Неинерциальные системы отсчёта
- 8.1 Расчёт домоседа
- 8.2 Расчёт путешественника
9 Выводы
10 См. также
11 Примечания
12 Источники
13 Дополнительная информация

История

Эффект релятивистского замедления времени был сформулирован Альбертом Эйнштейном в его работе 1905 года в виде следующей теоремы:

Если в точке А находятся двое синхронно идущих часов, и мы перемещаем одни из них по замкнутой кривой с постоянной скоростью до тех пор, пока они не вернутся в А (на что потребуется, скажем, t сек), то эти часы по прибытии в А будут отставать по сравнению с часами, остававшимися неподвижными…[1]

В форме парадокса этот эффект сформулировал в 1911 году Поль Ланжевен [2]. Придание парадоксу наглядной истории космического путешествия сделало его популярным, в том числе и в ненаучных кругах. Сам Ланжевен считал, что объяснение парадокса связано с ускоренным движением путешественника, которое необходимо для его возвращения на Землю.

Следующим анализ парадокса предпринял Макс фон Лауэ в 1913 году[3]. С его точки зрения важны не этапы ускорения путешественника, а сам факт смены им инерциальной системы отсчёта при возвращении на Землю.

После создания Общей теории относительности Альберт Эйнштейн в 1918 году объяснил парадокс при помощи факта влияния гравитационного поля на ход времени[4].

В самом деле, согласно общей теории относительности, часы идут тем медленнее, чем больше гравитационный потенциал в том месте, где они находятся.

Затем, в 1921 году простое объяснение, основанное на инвариантности собственного времени, предложилВольфганг Паули [5].

Некоторое время «парадокс близнецов» почти не привлекал к себе внимания. В 1956—1959 годах Герберт Дингл выступил с рядом статей[6][7],в которых утверждалось, что известные объяснения «парадокса» неверны. Несмотря на ошибочность аргументации Дингла[8][9], его работы вызвали многочисленные дискуссии в научных и научно-популярных журналах[10][11][12][13][14][15][16][17]. В результате появился ряд книг, посвящённых этой теме. Из русскоязычных источников стоит отметить книги[18][19][20][21], а также статью[22].

Большинство исследователей не считают «парадокс близнецов» демонстрацией противоречия теории относительности, хотя история появления тех или иных объяснений «парадокса» и придания ему новых форм не прекращается до настоящего времени[23][24][25][26][27].

Классификация объяснений парадокса

Объяснить парадокс, подобный «парадоксу близнецов», можно при помощи двух подходов:

1) Выявить происхождение логической ошибки в рассуждениях, которые привели к противоречию;

2) Провести детальные вычисления величины эффекта замедления времени с позиции каждого из братьев.

Первый подход зависит от деталей формулировки парадокса. В разделах «Простейшие объяснения» и «Физическая причина парадокса» будут приведены различные версии «парадокса» и даны объяснения того, почему противоречия на самом деле не возникает.

В рамках второго подхода расчёты показаний часов каждого из братьев проводятся как с точки зрения домоседа (что обычно не представляет труда), так и с точки зрения путешественника. Так как последний менял свою систему отсчёта, возможны различные варианты учёта этого факта. Их условно можно разделить на две большие группы.

К первой группе относятся вычисления на основе специальной теории относительности в рамках инерциальных систем отсчёта. В этом случае этапы ускоренного движения считаются пренебрежимо малыми по сравнению с общим временем полёта. Иногда вводится третья инерциальная система отсчёта, движущаяся навстречу путешественнику, при помощи которой показания его часов «передаются» брату-домоседу. В разделе «Обмен сигналами» будет приведен простейший расчёт, основанный на эффекте Доплера.

Ко второй группе относятся вычисления, учитывающие детали ускоренного движения. В свою очередь, они делятся по признаку использования или неиспользования в них теориигравитации Эйнштейна (ОТО). Расчёты с использованием ОТО основаны на введении эффективного гравитационного поля, эквивалентного ускорению системы, и учёте изменения в нём темпа хода времени. Во втором способе неинерциальные системы отсчёта описываются в плоском пространстве-времени и понятие гравитационного поля не привлекается. Основные идеи этой группы расчётов будут представлены в разделе «Неинерциальные системы отсчёта».

Кинематические эффекты СТО

В основе СТО лежат преобразования Лоренца.Для понимания сути парадокса близнецов необходим аккуратный анализ основных кинематических эффектов, которые из них следуют. Рассмотрим две системы отсчёта S{displaystyle textstyle S}

$textstyle S$ и S′{displaystyle textstyle S’} $textstyle S'$ , пространственные оси которых параллельны друг другу. Пусть система S′{displaystyle textstyle S’} $textstyle S'$ движется относительно S{displaystyle textstyle S} $textstyle S$ вдоль оси x{displaystyle textstyle x} $textstyle x$ со скоростью v{displaystyle textstyle v} $textstyle v$ , тогда:

x′=x−vt1−v2/c2,t′=t−vx/c21−v2/c2,{displaystyle x’={frac {x-vt}{sqrt {1-v^{2}/c^{2}}}},;;;;;;;;;;;;;t’={frac {t-vx/c^{2}}{sqrt {1-v^{2}/c^{2}}}},}

x'=frac{x-vt}{sqrt{1-v^2/c^2}},;;;;;;;;;;;;;t'=frac{t-vx/c^2}{sqrt{1-v^2/c^2}},

где (x,t){displaystyle textstyle (x,t)}

$textstyle (x,t)$ — координата и время в «неподвижной» системе отсчёта S{displaystyle textstyle S} $textstyle S$ , (x′,t′){displaystyle textstyle (x’,t’)} $textstyle (x',t')$ — координата и время в «движущейся» системе S′{displaystyle textstyle S’} $textstyle S'$ .

Замедление времени

Если часы неподвижны в системе S′{displaystyle textstyle S’}

$textstyle S'$ (в собственной системе отсчета), то для двух последовательных событий, происходящих в некоторой точке системы S′{displaystyle textstyle S’} $textstyle S'$ , выполнено равенство Δx′=0{displaystyle textstyle Delta x’=0} $textstyle Delta x'=0$ . Такие часы перемещаются относительно системы S{displaystyle textstyle S} $textstyle S$ по закону Δx=vΔt{displaystyle textstyle Delta x=vDelta t} $textstyle Delta x=vDelta t$ . Тогда из преобразований Лоренца следует, что интервал времени Δt′{displaystyle textstyle Delta t’} $textstyle Delta t'$ между событиями в системе S′{displaystyle textstyle S’} $textstyle S'$ связан с интервалом Δt{displaystyle textstyle Delta t} $textstyle Delta t$ между теми же событиями в системе S{displaystyle textstyle S} $textstyle S$ равенством: Δt′=Δt⋅1−v2/c2.{displaystyle ~~~Delta t’=Delta tcdot {sqrt {1-v^{2}/c^{2}}}.} ${displaystyle ~~~Delta t'=Delta tcdot {sqrt {1-v^{2}/c^{2}}}.}$

Важно понимать, что в этой формуле интервал времени Δt′{displaystyle textstyle Delta t’}

$textstyle Delta t'$ измеряется одними покоящимися в S′{displaystyle textstyle S’} $textstyle S'$ часами (Δx′=0{displaystyle textstyle Delta x’=0} $textstyle Delta x'=0$ ). Он сравнивается с показаниями Δt{displaystyle textstyle Delta t} $textstyle Delta t$ нескольких различных, синхронно идущих часов, расположенных в системе S{displaystyle textstyle S} $textstyle S$ (Δx≠0{displaystyle textstyle Delta xneq 0} ${displaystyle textstyle Delta xneq 0}$ ), мимо которых пролетают со скоростью v{displaystyle v} $v$ часы S′{displaystyle textstyle S’} $textstyle S'$ .

Интервал времени Δt{displaystyle textstyle Delta t}

$textstyle Delta t$ , измеренный часами в системе S{displaystyle textstyle S} $textstyle S$ между событиями в системе S′{displaystyle textstyle S’} $textstyle S'$ , больше интервала Δt′{displaystyle textstyle Delta t’} $textstyle Delta t'$ , измеренного часами в собственной системе отсчета S′{displaystyle textstyle S’} $textstyle S'$ : Δt>Δt′{displaystyle textstyle Delta t>textstyle Delta t’} ${displaystyle textstyle Delta t>textstyle Delta t'}$ , поскольку

Δt=Δt′1−v2c2{displaystyle ~~~~~~~~~~~~~~~~~~~Delta t={frac {Delta t’}{sqrt {1-{frac {v^{2}}{c^{2}}}}}}}

${displaystyle ~~~~~~~~~~~~~~~~~~~Delta t={frac {Delta t'}{sqrt {1-{frac {v^{2}}{c^{2}}}}}}}$ .

В системе S{displaystyle textstyle S}

$textstyle S$ движущиеся часы S′{displaystyle textstyle S’} $textstyle S'$ идут медленнее, чем в собственной системе отсчета S′{displaystyle textstyle S’} $textstyle S'$ .

Важный момент эффекта замедления времени связан с эквивалентностью инерциальных систем отсчёта (принцип относительности). Часы, неподвижные в системе S{displaystyle textstyle S}

$textstyle S$ : Δx=0{displaystyle textstyle Delta x=0} $textstyle Delta x=0$ , движутся относительно синхронизированных часов в системе S′{displaystyle textstyle S’} $textstyle S'$ : Δx′=−vΔt′{displaystyle textstyle Delta x’=-vDelta t’} $textstyle Delta x'=-vDelta t'$ и идут в S′{displaystyle textstyle S’} $textstyle S'$ медленнее, чем в собственной системе отсчета S{displaystyle textstyle S} $textstyle S$ : Δt′>Δt{displaystyle textstyle Delta t’>textstyle Delta t} ${displaystyle textstyle Delta t'>textstyle Delta t}$ , поскольку Δt′=Δt1−v2c2{displaystyle ~~~~~~~~~~~~~~~~~~~Delta t’={frac {Delta t}{sqrt {1-{frac {v^{2}}{c^{2}}}}}}} ${displaystyle ~~~~~~~~~~~~~~~~~~~Delta t'={frac {Delta t}{sqrt {1-{frac {v^{2}}{c^{2}}}}}}}$ .

Несмотря на прежние обозначения, последняя формула не противоречит предыдущей. Каждая из них описывает разные измерительные процедуры. В первом случае одни часы, покоящиеся в системе S′{displaystyle textstyle S’}

$textstyle S'$ (собственной системе отсчета), движутся мимо нескольких часов в S{displaystyle textstyle S} $textstyle S$ , а во втором случае ситуация обратная: одни часы в собственной системе отсчета S{displaystyle textstyle S} $textstyle S$ движутся мимо нескольких часов в S′{displaystyle textstyle S’} $textstyle S'$ .

Относительность одновременности

Относительность одновременности событий является ключевым эффектом СТО, необходимым для понимания «парадокса близнецов». Рассмотрим несколько синхронизированных часов, расположенных вдоль оси x{displaystyle textstyle x}

$textstyle x$ в каждой из систем отсчёта. Пусть рядом с каждыми часами в обеих системах отсчёта находятся наблюдатели. В преобразованиях Лоренца предполагается, что в момент времени t′=t=0{displaystyle textstyle t’=t=0} $textstyle t'=t=0$ начала систем отсчёта совпадают: x′=x=0{displaystyle textstyle x’=x=0} $textstyle x'=x=0$ . Ниже изображена такая синхронизация отсчёта времени (на «центральных» часах) с точки зрения наблюдателей в системе отсчёта S′{displaystyle textstyle S’} $textstyle S'$ (левый рисунок) и с точки зрения наблюдателей в S{displaystyle textstyle S} $textstyle S$ (правый рисунок):

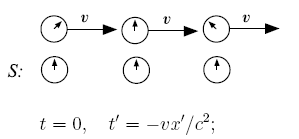
Положив в преобразованиях Лоренца t′=0{displaystyle textstyle t’=0}

$textstyle t'=0$ , получим t=vx/c2{displaystyle textstyle t=vx/c^{2}} $textstyle t=vx/c^2$ . Это означает, что наблюдатели в системе S′{displaystyle textstyle S’} $textstyle S'$ , одновременно с совпадением времени на центральных часах, регистрируют различные показания на часах в системе S{displaystyle textstyle S} $textstyle S$ (левый рисунок). Для наблюдателей в S′{displaystyle textstyle S’} $textstyle S'$ , расположенных справа от точки x=0{displaystyle textstyle x=0} $textstyle x=0$ , с координатами x>0{displaystyle textstyle x>0} $textstyle x>0$ , в момент времени t′=0{displaystyle textstyle t’=0} $textstyle t'=0$ часы неподвижной системы отсчёта S{displaystyle textstyle S} $textstyle S$ показывают «будущее» время: t=vx/c2>0{displaystyle textstyle t=vx/c^{2}>0} $textstyle t=vx/c^2>0$ . Наблюдатели S′{displaystyle textstyle S’} $textstyle S'$ , находящиеся слева от x=0{displaystyle textstyle x=0} $textstyle x=0$ , фиксируют «прошлое» время часов S{displaystyle textstyle S} $textstyle S$ : t<0{displaystyle textstyle t<0} $textstyle t<0$ . Положение стрелок символизирует разницу показаний часов двух систем отсчёта. Например, два события, произошедшие в момент t′=0{displaystyle textstyle t’=0} $textstyle t'=0$ в разных точках системы S′{displaystyle textstyle S’} $textstyle S'$ , происходят не одновременно в системе отсчета S{displaystyle textstyle S} $textstyle S$ с точки зрения наблюдателей в системе S′{displaystyle textstyle S’} $textstyle S'$ : левое событие происходит раньше правого. Действительно, для любого момента времени t′{displaystyle t’} $t'$ из преобразований Лоренца следует, что если Δt′=0{displaystyle Delta t’=0} $Delta t'=0$ , то Δt=vc2Δx.{displaystyle Delta t={frac {v}{c^{2}}}Delta x.} $Delta t={frac {v}{c^{2}}}Delta x.$ Отсюда, если Δx=x2−x1>0{displaystyle Delta x=x_{2}-x_{1}>0} $Delta x=x_{2}-x_{1}>0$ , то и Δt=t2−t1>0{displaystyle Delta t=t_{2}-t_{1}>0} $Delta t=t_{2}-t_{1}>0$ . Это означает, что в системе отсчета S{displaystyle textstyle S} $textstyle S$ левое событие в точке x1{displaystyle x_{1}} $x_{1}$ , x1<x2{displaystyle x_{1}<x_{2}} $x_{1}<x_{2}$ , происходит раньше правого в точке x2{displaystyle x_{2}} $x_{2}$ : t1<t2{displaystyle t_{1}<t_{2}} ${displaystyle t_{1}<t_{2}}$ . Этот факт фиксируется часами, синхронизироваными в системе S{displaystyle textstyle S} $textstyle S$ . С точки зрения наблюдателей S{displaystyle textstyle S} $textstyle S$ часы в системе S′{displaystyle textstyle S’} $textstyle S'$ не синхронизированы .

Единое «настоящее», то есть часы, синхронно идущие в различных точках пространства, можно ввести в каждой инерциальной системе отсчёта. Однако единого «настоящего» для двух различных систем отсчёта не существует.

Движущаяся относительно неподвижных наблюдателей система с их точки зрениясодержит рассинхронизированные в направлении движения часы, своеобразноенепрерывное объединение «прошлого», «настоящего» и «будущего».

Эффекты замедления времени и относительности одновременности тесно связаны друг с другом и одинаково необходимы для расчёта ситуации, описанной в «парадоксе» близнецов.

Простейшие объяснения

Благодаря своей продолжительной истории парадокс близнецов существует в разнообразных формулировках. Чаще всего тем или иным методом демонстрируется симметричность братьев, из которой должно было бы следовать противоречие с выводом СТО о том, что отстанут часы путешественника. Исходная версия парадокса (Формулировка I) не уточняет характера движения путешественника. Поэтому для неё справедливо следующее простое объяснение (на качественном уровне):

Объяснение I. Братья не являются равноправными, так как один из них (путешественник) испытывал этапы ускоренного движения, необходимые для его возвращения на Землю[2].

Однако, как показывают экспериментальные данные, ускорение как таковое не влияет на скорость хода часов[28]. Таким образом, в данном случае ускорение является всего лишь индикатором некоторого явления, которое вносит асимметрию в состояния путешественника и домоседа.

Конечно, сама по себе констатация несимметричности братьев не объясняет, почему замедлиться должны часы именно у путешественника, а не у домоседа. Кроме этого, часто возникает непонимание:

Рис. 1. Парадокс близнецов с точки зрения инерциальной системы отсчёта, связанной с Землёй Рис. 2. Парадокс близнецов с точки зрения инерциальной системы отсчёта, на первой половине пути совпадающей c удаляющимся кораблём

«Почему нарушение равноправия братьев в течение столь короткого времени (остановка путешественника) приводит к такому разительному нарушению симметрии?»

Наглядно это можно увидеть на рис. 1 и 2, где показана одна и та же ситуация с разных точек зрения. На рис. 1 рассматривается инерциальная система отсчёта, связанная с Землёй. Рис. 2 показывает инерциальную систему отсчёта, связанную с кораблём. Однако поскольку корабль не всё время движется равномерно (условно считаем, что его путь состоит из двух участков равномерного движения, разделёнными кратковременным ускорением), то инерциальная система отсчёта может совпадать с кораблём только часть его пути. Рассматриваем систему, которая совпадает с кораблём на первой половине его путешествия.

Как видно из рис. 1 и 2:

В обоих случаях мировая линия Земли является прямой.
В обоих случаях мировая линия корабля является ломаной линией.

Поскольку ломаная в любой системе отсчёта длиннее прямой, то путешественник проходит в пространстве-времени больший путь, а большему пути соответствует меньшее собственное время.

Чтобы глубже понять причины несимметричности и следствия, к которым они приводят, необходимо ещё раз выделить ключевые посылки, явно или неявно присутствующие в любой формулировке парадокса. Для этого будем считать, что вдоль траектории движения путешественника в «неподвижной» системе отсчёта, связанной с домоседом, расположены синхронно идущие (в этой системе) часы.Тогда возможна следующая цепочка рассуждений, как бы «доказывающих» противоречивость выводов СТО:

Путешественник, пролетая мимо любых часов, неподвижных в системе домоседа, наблюдает их замедленный ход.
Более медленный темп хода часов означает, что их накопленные показания отстанут от показаний часов путешественника, и при длительном полёте — сколь угодно сильно.
Быстро остановившись, путешественник по-прежнему должен наблюдать отставание часов, расположенных в «точке остановки».
Все часы в «неподвижной» системе идут синхронно, поэтому отстанут и часы брата на Земле, что противоречит выводу СТО.

Итак, почему путешественник на самом деле будет наблюдать отставание своих часов от часов «неподвижной» системы, несмотря на то, что все такие часы с его точки зрения идут медленнее? Наиболее простым объяснением[29] в рамках СТО является то, что синхронизовать все часы в двух инерциальных системах отсчёта невозможно. Рассмотрим это объяснение подробнее.

Физическая причина парадокса

Во время полёта путешественник и домосед находятся в различных точках пространства и не могут сравнивать свои часы непосредственно. Поэтому, как и выше, будем считать, что вдоль траектории движения путешественника в «неподвижной» системе, связанной с домоседом, расставлены одинаковые, синхронно идущие часы, которые может наблюдать путешественник во время полёта. Благодаря процедуре синхронизации в «неподвижной» системе отсчёта введено единое время, определяющее в данный момент «настоящее» этой системы.

После старта путешественник «переходит» в инерциальную систему отсчёта S′{displaystyle textstyle S’}

$textstyle S'$ , движущуюся относительно «неподвижной» S{displaystyle textstyle S} $textstyle S$ со скоростью v{displaystyle textstyle v} $textstyle v$ . Этот момент времени принимается братьями за начальный t=t′=0{displaystyle textstyle t=t’=0} $textstyle t=t'=0$ . Каждый из них будет наблюдать замедленный ход часов другого брата.

Однако, единое «настоящее» системы S{displaystyle textstyle S}

$textstyle S$ для путешественника перестаёт существовать. В системе отсчёта S′{displaystyle textstyle S’} $textstyle S'$ есть своё «настоящее» (множество синхронизированных часов). Для системы S′{displaystyle textstyle S’} $textstyle S'$ , чем дальше по ходу движения путешественника находятся части системы S{displaystyle textstyle S} $textstyle S$ , тем в более отдалённом «будущем» (с точки зрения «настоящего» системы S′{displaystyle textstyle S’} $textstyle S'$ ) они находятся.

Непосредственно это будущее наблюдать путешественник не может. Это могли бы сделать другие наблюдатели системы S′{displaystyle textstyle S’}

$textstyle S'$ , расположенные впереди по движению и имеющие синхронизированное с путешественником время.

Поэтому, хотя все часы в неподвижной системе отсчёта, мимо которых пролетает путешественник, идут с его точки зрения медленнее, из этого не следует, что они отстанут от его часов.

В момент времени t′=0{displaystyle textstyle t’=0}

$textstyle t'=0$ , чем дальше впереди по курсу находятся «неподвижные» часы, тем больше их показания с точки зрения путешественника.Когда он достигает этих часов, они не успеют отстать настолько, чтобы скомпенсировать начальное расхождение времени.

Действительно, положим координату путешественника в преобразованиях Лоренца равной x′=0{displaystyle textstyle x’=0}

$textstyle x'=0$ . Закон его движения относительно системы S{displaystyle textstyle S} $textstyle S$ имеет вид x=vt{displaystyle textstyle x=vt} $textstyle x=vt$ . Время, прошедшее после начала полёта, по часам в системе S′{displaystyle textstyle S’} $textstyle S'$ меньше, чем в S{displaystyle textstyle S} $textstyle S$ : t′<t{displaystyle t'<t} $t'<t$ , так как

t′=t−v(vt)/c21−v2/c2=t1−v2/c2.{displaystyle t’={frac {t-v(vt)/c^{2}}{sqrt {1-v^{2}/c^{2}}}}=t,{sqrt {1-v^{2}/c^{2}}}.} ${displaystyle t'={frac {t-v(vt)/c^{2}}{sqrt {1-v^{2}/c^{2}}}}=t,{sqrt {1-v^{2}/c^{2}}}.}$

Другими словами, время на часах путешественника t′{displaystyle t’}

$t'$ отстаёт от показаний часов t{displaystyle t} $t$ системы S{displaystyle S} $S$ . В то же время часы, мимо которых пролетает путешественник, неподвижны в S{displaystyle textstyle S} $textstyle S$ : Δx=0{displaystyle textstyle Delta x=0} $textstyle Delta x = 0$ . Поэтому их темп хода для путешественника выглядит замедленным:

Δt′=Δt1−v2/c2>Δt.{displaystyle Delta t’={frac {Delta t}{sqrt {1-v^{2}/c^{2}}}}>Delta t.}

Delta t' = frac{Delta t}{sqrt{1-v^2/c^2}} > Delta t.

Таким образом:

несмотря на то, что все конкретные часы в системе S{displaystyle textstyle S}

$textstyle S$ идут медленнее с точки зрения наблюдателя в S′{displaystyle textstyle S’} $textstyle S'$ , разные часы вдоль его траектории будут показывать время, ушедшее вперед.

Разность темпа хода часов Δt{displaystyle Delta t}

$Delta t$ и Δt′{displaystyle Delta t’} $Delta t'$ — эффект относительный, тогда как значения текущих показаний t{displaystyle t} $t$ и t′{displaystyle t’} $t'$ в одной пространственной точке — носят абсолютный характер. Наблюдатели, находящиеся в различных инерциальных системах отсчёта, но «в одной» пространственной точке, всегда могут сравнить текущие показания своих часов. Путешественник, пролетая мимо часов системы S{displaystyle textstyle S} $textstyle S$ видит, что они ушли вперёд t>t′{displaystyle textstyle t>t’} $textstyle t>t'$ . Поэтому, если путешественник решит остановиться (быстро затормозив), ничего не изменится, и он попадёт в «будущее» системы S{displaystyle textstyle S} $textstyle S$ . Естественно, после остановки темп хода его часов и часов в S{displaystyle textstyle S} $textstyle S$ станет одинаковым. Однако, часы путешественника будут показывать меньшее время чем часы системы S{displaystyle textstyle S} $textstyle S$ , находящиеся в точке остановки. В силу единого времени в системе S{displaystyle textstyle S} $textstyle S$ часы путешественника отстанут от всех часов S{displaystyle textstyle S} $textstyle S$ , в том числе и от часов его брата. После остановки путешественник может вернуться домой. В этом случае весь анализ повторяется. В результате, как в точке остановки и разворота, так и в исходной точке при возвращении путешественник оказывается моложе своего брата-домоседа.

Если же вместо остановки путешественника до его скорости ускорится домосед, то он «попадёт» в «будущее» системы путешественника. В результате «домосед» окажется моложе «путешественника». Таким образом:

кто изменяет свою систему отсчёта, тот и оказывается моложе.

Обмен сигналами

Возможно, эта статья содержит оригинальное исследование. Добавьте ссылки на источники, в противном случае она может быть выставлена на удаление. Соответствующую дискуссию можно найти на странице обсуждения. (19 октября 2017)

Вычисление замедления времени с позиции каждого брата можно провести при помощи анализа обмена сигналами между ними. Хотя братья, находясь в различных точках пространства, не могут непосредственно сравнивать показания своих часов, они могут передавать сигналы «точного времени» при помощи световых импульсов или видеотрансляции изображения часов. Понятно, что при этом они наблюдают не «текущее» время на часах брата, а «прошлое», так как сигналу требуется время для распространения от источника к приёмнику.

При обмене сигналами необходимо учитывать эффект Доплера. Если источник удаляется от приёмника, то частота сигнала уменьшается, а когда он приближается — увеличивается:

где ν0{displaystyle textstyle nu _{0}}

$textstyle nu_0$ — собственная частота излучения, а ν{displaystyle textstyle nu } $textstyle nu$ — частота принимаемого наблюдателем сигнала. Эффект Доплера имеет классическую составляющую и составляющую релятивистскую, непосредственно связанную с замедлением времени. Скорость v{displaystyle textstyle v} $textstyle v$ , входящая в соотношения изменения частоты, является относительной скоростью источника и приёмника.

Рассмотрим ситуацию, в которой братья передают друг другу каждую секунду ν0=1{displaystyle textstyle nu _{0}=1}

$textstyle nu_0=1$ (по своим часам) сигналы точного времени. Проведём сначала расчёт с позиции путешественника.

Расчёт путешественника

Пока путешественник удаляется от Земли, он, в силу эффекта Доплера, регистрирует уменьшение частоты принимаемых сигналов. Видеотрансляция с Земли выглядит более медленной. После быстрого торможения и остановки путешественник перестаёт удаляться от земных сигналов, и их период сразу[rmr 1] оказывается равным его секунде. Темп видеотрансляции становится «естественным», хотя, в силу конечности скорости света, путешественник по-прежнему наблюдает «прошлое» своего брата. Развернувшись и разогнавшись, путешественник начинает «набегать»[rmr 2] на идущие ему навстречу сигналы и их частота увеличивается (опять же в силу эффекта Доплера). «Движения брата» на видеотрансляции с этого момента начинают выглядеть для путешественника ускоренными[rmr 3].

Время полёта по часам путешественника в одну сторону равно t1′{displaystyle textstyle t’_{1}}

$textstyle t'_1$ , и такое же в обратную. Количество принятых «земных секунд» в течение путешествия t′=2t1′{displaystyle textstyle t’=2t’_{1}} $textstyle t'=2t'_1$ равно их частоте ν{displaystyle textstyle nu } $textstyle nu$ , умноженной на время. Поэтому при удалении от Земли путешественник получит существенно меньше «секунд»:

t1=t1′⋅c−vc+v<t1′,{displaystyle t_{1}=t’_{1}cdot {sqrt {frac {c-v}{c+v}}}<t’_{1},}

t_1 = t'_1cdot sqrt{frac{c-v}{c+v}} < t'_1,

а при приближении, наоборот, больше:

t2=t1′⋅c+vc−v>t1′.{displaystyle t_{2}=t’_{1}cdot {sqrt {frac {c+v}{c-v}}}>t’_{1}.}

t_2 =t'_1cdot sqrt{frac{c+v}{c-v}} > t'_1.

Суммарное количество «секунд», полученных с Земли за время t′=2t1′{displaystyle textstyle t’=2t’_{1}}

$textstyle t'=2t'_1$ , больше, чем переданных на неё:

t=t1+t2=t1′⋅c−vc2−v2+t1′⋅c+vc2−v2=t′1−v2/c2,{displaystyle t=t_{1}+t_{2}=t’_{1}cdot {frac {c-v}{sqrt {c^{2}-v^{2}}}}+t’_{1}cdot {frac {c+v}{sqrt {c^{2}-v^{2}}}}={frac {t’}{sqrt {1-v^{2}/c^{2}}}},}

t = t_1 + t_2 = t'_1cdot frac{c-v}{sqrt{c^2-v^2}} + t'_1cdot frac{c+v}{sqrt{c^2-v^2}}= frac{t'}{sqrt{1-v^2/c^2}},

в точном соответствии с формулой замедления времени.

Расчёт домоседа

Несколько иная арифметика у домоседа. Пока его брат удаляется, он также регистрирует увеличенный период точного времени, передаваемый путешественником. Однако, в отличие от брата, домосед наблюдает такое замедление дольше. Время полёта на расстояние L{displaystyle textstyle L}

$textstyle L$ в одну сторону составляет по земным часам t1{displaystyle textstyle t_{1}} $textstyle t_1$ . Торможение и разворот путешественника домосед увидит спустя дополнительное время t2=L/c{displaystyle textstyle t_{2}=L/c} $textstyle t_2=L/c$ , требуемое свету для прохождения расстояния L{displaystyle textstyle L} $textstyle L$ от точки разворота. Поэтому, только через время t1+t2{displaystyle textstyle t_{1}+t_{2}} $textstyle t_1+t_2$ от начала путешествия домосед зарегистрирует ускоренную работу часов[rmr 4] приближающегося брата: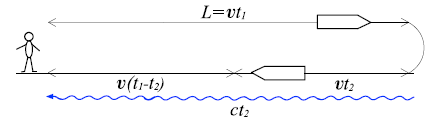

Время движения света от точки разворота выражается через время полёта к ней путешественника следующим образом (см. рисунок):

t2=Lc=vt1c.{displaystyle t_{2}={frac {L}{c}}={frac {vt_{1}}{c}}.}

t_2=frac{L}{c}=frac{vt_1}{c}.

Поэтому количество «секунд», полученных от путешественника, до момента его разворота (по наблюдениям домоседа) равно:

t1′=(t1+t2)⋅c−vc+v=t1⋅(1+vc)⋅c−vc+v=t1⋅1−v2c2.{displaystyle t’_{1}=(t_{1}+t_{2})cdot {sqrt {frac {c-v}{c+v}}}=t_{1}cdot left(1+{frac {v}{c}}right)cdot {sqrt {frac {c-v}{c+v}}}=t_{1}cdot {sqrt {1-{frac {v^{2}}{c^{2}}}}}.}

t'_1 = (t_1+t_2)cdotsqrt{frac{c-v}{c+v}} = t_1cdot left(1+frac{v}{c}right)cdotsqrt{frac{c-v}{c+v}} = t_1cdot sqrt{1-frac{v^2}{c^2}}.

Сигналы с повышенной частотой домосед принимает в течение времени t1−t2{displaystyle textstyle t_{1}-t_{2}}

$textstyle t_1-t_2$ (см. рисунок выше), и получает t2′{displaystyle textstyle t’_{2}} $textstyle t'_2$ «секунд» путешественника:

t2′=(t1−t2)⋅c+vc−v=t1⋅(1−vc)⋅c+vc−v=t1⋅1−v2c2.{displaystyle t’_{2}=(t_{1}-t_{2})cdot {sqrt {frac {c+v}{c-v}}}=t_{1}cdot left(1-{frac {v}{c}}right)cdot {sqrt {frac {c+v}{c-v}}}=t_{1}cdot {sqrt {1-{frac {v^{2}}{c^{2}}}}}.}

t'_2= (t_1-t_2) cdotsqrt{frac{c+v}{c-v}} = t_1cdot left(1-frac{v}{c}right)cdotsqrt{frac{c+v}{c-v}} = t_1cdot sqrt{1-frac{v^2}{c^2}}.

Суммарное число полученных «секунд» за время t=2t1{displaystyle textstyle t=2t_{1}}

$textstyle t=2t_1$ равно:

t′=t1′+t2′=t⋅1−v2/c2.{displaystyle t’=t’_{1}+t’_{2}=tcdot {sqrt {1-v^{2}/c^{2}}}.}

t'= t'_1+t'_2 = tcdotsqrt{1-v^2/c^2}.

Таким образом, соотношение для показания часов в момент встречи путешественника (t′{displaystyle textstyle t’}

$textstyle t'$ ) и брата-домоседа (t{displaystyle textstyle t} $textstyle t$ ) не зависит от того, с чьей точки зрения оно рассчитывается.

Геометрическая интерпретация

Иллюстрация парадокса близнецов на диаграмме Минковского.

В пространстве Минковского мировая линия покоящегося (или двигающегося равномерно и прямолинейно) наблюдателя является отрезком прямой. Мировая линия путешественника, улетевшего с Земли и возвратившегося к ней, прямой не является (в простейшем случае мгновенного изменения скорости на противоположную в точке поворота она является ломаной, а при прохождении части пути с постоянным ускорением соответствующий участок линии будет дугой гиперболы). Так же как в обычной геометрии из всех линий, соединяющих две точки, самой короткой является прямая, так же и в пространстве Минковского из всех мировых линий, соединяющих две точки, самой длинной (а не самой короткой в силу псевдоевклидовости пространства-времени) является отрезок прямой.

Поскольку длина мировой линии наблюдателя, переместившегося в пространстве Минковского из точки a в точку w, с точностью до множителя c равна времени, которое было затрачено на это перемещение в его собственной системе отсчёта, мы имеем, что из всех наблюдателей, стартовавших в точке a и финишировавших в точке w, в системе отсчёта того наблюдателя, который покоился (или двигался равномерно и прямолинейно, если пространственные координаты точек a и w не совпадают), пройдёт наибольшее время.

Неинерциальные системы отсчёта

В произвольных системах отсчёта свойства пространства и времени определяютсяметрическим тензором gμν{displaystyle textstyle g_{mu nu }}

$textstyle g_{munu}$ , задающиминтервал между двумя бесконечно близкими событиями:

ds2=gμνdxμdxν=g00(dx0)2+2g0idx0dxi+gijdxidxj,{displaystyle ds^{2}=g_{mu nu },dx^{mu }dx^{nu }=g_{00},(dx^{0})^{2}+2,g_{0i},dx^{0}dx^{i}+g_{ij},dx^{i}dx^{j},}

ds^2 = g_{munu},dx^mu dx^nu = g_{00}, (dx^0)^2 + 2,g_{0i},dx^0dx^i + g_{ij},dx^idx^j,

где по повторяющимся индексам подразумевается суммирование (по греческим буквам от 0 до 3, а по латинским от 1 до 3), x0=ct{displaystyle textstyle x^{0}=ct}

$textstyle x^0=ct$ — временная координата, xi=(x,y,z){displaystyle textstyle x^{i}=(x,y,z)} $textstyle x^i=(x,y,z)$ — пространственные. Собственное время часов вдоль их траектории определяется следующим образом:

1c∫0tds.{displaystyle {frac {1}{c}}int limits _{0}^{t}ds.}

frac{1}{c}intlimits^t_0 ds.

Его величина является инвариантом, следовательно, вычисления проведенные в различных системах отсчёта, должны давать один и тот же результат.

Расчёт домоседа

Близнец, оставшийся на Земле, находится в инерциальной системе отсчёта, поэтому для него метрика может быть выбрана таким образом, что

ds2=(cdt)2−(dx)2−(dy)2−(dz)2.{displaystyle ds^{2}=(cdt)^{2}-(dx)^{2}-(dy)^{2}-(dz)^{2}.}

ds^2=(cdt)^2-(dx)^2-(dy)^2-(dz)^2.

В этом случае собственное время любых часов принимает простой вид:

∫0t1−u2(t)/c2⋅dt,{displaystyle int limits _{0}^{t}{sqrt {1-mathbf {u} ^{2}(t)/c^{2}}}cdot dt,}

intlimits^t_0sqrt{1-mathbf{u}^2(t)/c^2}cdot dt,

где u(t){displaystyle textstyle mathbf {u} (t)}

$textstyle mathbf{u}(t)$ — скорость этих часов. Земные часы неподвижны (u=0{displaystyle textstyle mathbf {u} =0} $textstyle mathbf{u}=0$ ), и их собственное время равно координатному τ0=t{displaystyle textstyle tau _{0}=t} $textstyle tau_0=t$ .Часы путешественника имеют переменную скорость u(t){displaystyle textstyle mathbf {u} (t)} $textstyle mathbf{u}(t)$ .Так как корень под интегралом остаётся всё время меньше единицы, время этих часов, независимо от явного вида функции u(t){displaystyle textstyle mathbf {u} (t)} $textstyle mathbf{u}(t)$ , всегда оказываются меньшеt{displaystyle textstyle t} $textstyle t$ . В результате τ0′<τ0{displaystyle textstyle tau ‘_{0}<tau _{0}} $textstyle tau'_0<tau_0$ .

Если разгон и торможение проходят релятивистски равноускоренно (с параметром собственного ускорения a{displaystyle textstyle a}

$textstyle a$ ) в течение τ1{displaystyle tau _{1}} $tau_1$ , а равномерное движение — τ2{displaystyle tau _{2}} $tau_2$ , то по часам корабля пройдёт время[30]:

τ0=2caln⁡[aτ1c+1+(aτ1c)2]+τ21+(aτ1/c)2=2caarcsinh⁡aτ1c+τ21+(aτ1/c)2{displaystyle tau _{0}={frac {2c}{a}},ln left[{frac {atau _{1}}{c}}+{sqrt {1+left({frac {atau _{1}}{c}}right)^{2}}}right]+{frac {tau _{2}}{sqrt {1+(atau _{1}/c)^{2}}}}={frac {2c}{a}},operatorname {arcsinh} {frac {atau _{1}}{c}}+{frac {tau _{2}}{sqrt {1+(atau _{1}/c)^{2}}}}}

tau_0 = frac{2c}{a},lnleft[frac{atau_1}{c}+sqrt{1+left(frac{atau_1}{c}right)^2}right] + frac{tau_2}{sqrt{1+(atau_1/c)^2}} = frac{2c}{a}, operatorname{arcsinh}frac{atau_1}{c} + frac{tau_2}{sqrt{1+(atau_1/c)^2}}

, где arcsinh{displaystyle operatorname {arcsinh} }

operatorname{arcsinh}

— гиперболический арксинус

Рассмотрим гипотетический полёт к звёздной системе Альфа Центавра, удалённой от Земли на расстояние в 4,3 световых года. Если время измеряется в годах, а расстояния в световых годах, то скорость света c{displaystyle textstyle c}

$textstyle c$ равна единице, а единичное ускорение a=1{displaystyle textstyle a=1} $textstyle a=1$ св.год/год² близко кускорению свободного падения и примерно равно 9,5 м/c².

Пусть половину пути космический корабль двигается с единичным ускорением, а вторую половину — с таким же ускорением тормозит (τ2=0{displaystyle textstyle tau _{2}=0}

$textstyle tau_2=0$ ). Затем корабль разворачивается и повторяет этапы разгона и торможения. В этой ситуации время полёта в земной системе отсчёта составит примерно 12 лет, тогда как по часам на корабле пройдёт 7,3 года. Максимальная скорость корабля достигнет 0,95 от скорости света.

За 64 года собственного времени космический корабль с единичным ускорением потенциально может совершить путешествие (вернувшись на Землю) к галактике Андромеды, удалённой на 2,5 млн св. лет. На Земле за время такого полёта пройдёт около 5 млн лет. Развивая вдвое большее ускорение (к которому тренированный человек вполне может привыкнуть при соблюдении ряда условий и использования ряда приспособлений, например, анабиоза), можно подумать даже об экспедиции к видимому краю Вселенной (около 14 млрд. св. лет), которая займёт у космонавтов порядка 50 лет; правда, возвратившись из такой экспедиции (через 28 млрд. лет по земным часам), её участники рискуют не застать в живых не то что Землю и Солнце, но даже нашу Галактику. Исходя из этих расчётов, разумный радиус доступности для межзвёздных экспедиций с возвратом не превышает нескольких десятков световых лет, если, конечно, не будут открыты какие-либо принципиально новые физические принципы перемещения в пространстве-времени. Впрочем, обнаружение многочисленных экзопланет даёт основания полагать, что планетные системы встречаются у достаточно большой доли звёзд, поэтому космонавтам будет что исследовать и в этом радиусе (например, планетные системы ε Эридана и Глизе 581).

Расчёт путешественника

Для проведения того же расчёта с позиции путешественника, необходимо задать метрический тензор, соответствующий его неинерциальной системе отсчёта. Относительно этой системы скорость путешественника нулевая, поэтому время на его часах равно

τ0′=∫0tg00dt.{displaystyle tau ‘_{0}=int limits _{0}^{t}{sqrt {g_{00}}};dt.}

tau'_0=intlimits^t_0sqrt{g_{00}};dt.

Заметим, что t{displaystyle textstyle t}

$textstyle t$ является координатным временем и в системе путешественника отличается от времени t{displaystyle textstyle t} $textstyle t$ системы отсчёта домоседа.

Земные часы свободны, поэтому они движутся вдоль геодезической, определяемой уравнением[31]:

d2xμds2+Γνλμdxνdsdxλds=0,{displaystyle {frac {d^{2}x^{mu }}{ds^{2}}}+Gamma _{nu lambda }^{mu },{frac {dx^{nu }}{ds}}{frac {dx^{lambda }}{ds}}=0,}

frac{d^2x^mu}{ds^2}+Gamma^mu_{nulambda},frac{dx^nu}{ds}frac{dx^lambda}{ds}=0,

где Γνλμ{displaystyle textstyle Gamma _{nu lambda }^{mu }}

$textstyle Gamma^mu_{nulambda}$ — символы Кристоффеля,выражающиеся через метрический тензор gμν{displaystyle textstyle g_{mu nu }} $textstyle g_{munu}$ .При заданном метрическом тензоре неинерциальной системы отсчёта эти уравнения позволяют найти траекториюxi(t){displaystyle textstyle x^{i}(t)} $textstyle x^i(t)$ часов домоседа в системе отсчёта путешественника.Её подстановка в формулу для собственного времени даёт интервал времени, прошедший по «неподвижным» часам:

τ0=∫0tg00+2g0iui/c+gijuiuj/c2⋅dt,{displaystyle tau _{0}=int limits _{0}^{t}{sqrt {g_{00}+2g_{0i},u^{i}/c+g_{ij},u^{i}u^{j}/c^{2}}}cdot dt,}

tau_0 = intlimits^t_0 sqrt{g_{00} + 2g_{0i},u^i/c + g_{ij},u^iu^j/c^2}cdot dt,

где ui(t)=dxi/dt{displaystyle textstyle u^{i}(t)=dx^{i}/dt}

$textstyle u^i(t)=dx^i/dt$ — координатная скорость земных часов.

Подобное описание неинерциальных систем отсчёта возможно либо при помощитеории гравитации Эйнштейна,либо без ссылки на последнюю. Детали расчёта в рамках первого способа можно найти, например, в книге Фока [32] или Мёллера [33]. Второй способ рассмотрен в книге Логунова [34].

Результат всех этих вычислений показывает, что и с точки зрения путешественника его часы отстанут от часов неподвижного наблюдателя. В итоге разница времени путешествия с обеих точек зрения будет одинаковая, и путешественник окажется моложе домоседа. Если длительность этапов ускоренного движения много меньше длительности равномерного полёта, то результат более общих вычислений совпадает с формулой, полученной в рамках инерциальных систем отсчёта.

Выводы

Рассуждения, проводимые в истории с близнецами, приводят только к кажущемуся логическому противоречию. При любой формулировке «парадокса» полной симметричности между братьями нет. Кроме этого, важную роль для понимания того, почему время замедляется именно у путешественника, менявшего свою систему отсчёта, играет относительность одновременности событий.

Расчёт величины замедления времени с позиции каждого брата может быть выполнен как в рамках элементарных вычислений в СТО, так и при помощи анализа неинерциальных систем отсчёта. Все эти вычисления согласуются друг с другом и показывают, что путешественник окажется моложе своего брата-домоседа.

Парадоксом близнецов ошибочно часто также называют сам вывод теории относительности о том, что один из близнецов состарится сильнее другого. Хотя такая ситуация и необычна, в ней нет внутреннего противоречия. Многочисленные эксперименты по удлинению времени жизни элементарных частиц и замедлению хода макроскопических часов при их движении подтверждают теорию относительности. Это даёт основание утверждать, что замедление времени, описанное в истории с близнецами, произойдёт и при реальном осуществлении этого мысленного эксперимента.

См. также

Примечания

↑ Здесь свет рассматривается в ИСО, то есть в системе домоседа, а не путешественника
↑ «Набегать» с точки зрения домоседа. Относительно путешественника источник излучения (домосед) летит навстречу.
↑ Имеется в виду ускоренный приём сигнала, тем не менее, с точки зрения путешественника, весь мир домоседа замедлен в соответствии с релятивистским замедлением времени.
↑ Имеется в виду увеличенная скорость приёма импульсов путешественника из-за его движения навстречу.

Источники

↑ Эйнштейн А. «К электродинамике движущихся тел», Ann. d. Phys.,1905 b. 17, s. 89, русский перевод в «Эйнштейн А. Собрание научных трудов в четырёх томах. Том 1. Работы по теории относительности 1905—1920.» М.: Наука, 1965.
↑ 1 2 Langevin P. «L’evolution de l’espace et du temps». Scientia 10: 31-54. (1911)
↑ Laue M. (1913) «Das Relativit»atsprinzip». Wissenschaft (No. 38) (2 ed.). (1913)
↑ Эйнштейн А. «Диалог по поводу возражений против теории относительности», Naturwiss., 6, с.697—702. (1918). русский перевод «А. Эйнштейн, Собрание научных трудов», т. I, М., «Наука» (1965)
↑ Паули В. — «Теория Относительности» М.: Наука, 1991.
↑ Dingle Н. «Relativity and Space travel», Nature 177, 4513 (1956).
↑ Dingle H. «A possible experimental test of Einstein’s Second postulate», Nature 183, 4677 (1959).
↑ Coawford F. «Experimental verification of the clock-paradox in relativity», Nature 179, 4549 (1957).
↑ Darvin S. , «The clock paradox in relativity», Nature 180, 4593 (1957).
↑ Бойер Р. , «Парадокс часов и общая теория относительности», Эйнштейновский сборник, «Наука», (1968).
↑ Campbell W. , «The clock paradox», Canad. Aeronaut. J.4, 9, (1958)
↑ Frey R., Brigham V., «Paradox of the twins», Amer. J. Phys. 25, 8 (1957)
↑ Leffert С. , Donahue T., «Clock paradox and the physics of discontinuous gravitational fields», Amer. J. Phys. 26, 8 (1958)
↑ McMillan E., «The „clock-paradox“ and Space travel», Science, 126, 3270 (1957)
↑ Romer R. , «Twin paradox in special relativity». Amer. J. Phys. 27, 3 (1957)
↑ Schild, A. «The clock paradox in relativity theory», Amer. Math. Mouthly 66, 1, 1-8 (1959).
↑ Singer S., «Relativity and space travel», Nature 179,4567 (1957)
↑ Скобельцын Д. В., «Парадокс близнецов в теории относительности», «Наука», (1966).
↑ Гольденблат И. И., «Парадоксы времени в релятивистской механике», М. «Наука», (1972).
↑ Терлецкий Я. П. «Парадоксы теории относительности», М.: Наука (1965)
↑ Угаров В. А. — «Специальная теория относительности» М.: «Наука», (1977)
↑ Борн М., «Космические путешествия и парадокс часов», УФН, 69, вып. 1 (1959)
↑ Dray T., «The twin paradox revisited» Amer. J. of Phys. V.58, I.9, pp.822-825 (1990)
↑ Debs T.A.. Redhead, M.L.G. «Paradox of the twins» Amer. J. of Phys. V.64; N.4, pp.384-391, (1996)
↑ Cranor M.B., Heider E.M., Price R.H. «A circular twin paradox» Amer. J. of Phys. V.68; P.11, pp.1016-1020 (2000)
↑ Muller T., King A., Adis D., «A trip to the end of the universe and the twin paradox» Amer. J. of Phys. V.76; N.4/5, pp.360-373 (2008)
↑ Grandou T., Rubin J.L., «On the Ingredients of the Twin Paradox» Int.J. of Theor. Phys., V. 48, N.1, pp.101-114 (2009)
↑ Мизнер Ч., Торн К., Уилер Дж. § 38.4. ПРОВЕРКИ СУЩЕСТВОВАНИЯ МЕТРИКИ, ОПРЕДЕЛЯЮЩЕЙ ИЗМЕРЕНИЯ ДЛИНЫ И ВРЕМЕНИ, А ТАКЖЕ КИНЕМАТИКУ ЧАСТИЦ // Гравитация. — М.: Мир, 1977. — Т. 3. — С. 296. — 512 с.
↑ Парадокс близнецов
↑ Ускоренное движение в специальной теории относительности, сайт «Релятивистский мир — лекции по теории относительности, гравитации и космологии»
↑ Шаблон:Книга:Ландау Л.Д., Лифшиц Е.М.: Теория поля
↑ Фок В. А. «Теория Пространства, Времени и Тяготения» М.: Гос.изд.тех.-теор.лит., (1955)
↑ Мёллер К. «Теория относительности» М.: «Атомиздат», 1975.
↑ Логунов А. А., «Лекции по теории относительности и гравитации. Современный анализ проблемы», М.:» Наука» (1987)

Дополнительная информация

Twin Paradox overview in the Usenet Physics FAQ (англ.)
Wolfgang Rindler, Wolfgang Rindler. Time dilation // Relativity: Special, General, and Cosmological. — Oxford University Press, 2006. — P. 43. — ISBN 0198567316.
FLASH Animations: from John de Pillis. (Scene 1): «View» from the Earth twin’s point of view. (Scene 2): «View» from the traveling twin’s point of view. (англ.)
Время в теории относительности / Сайт Релятивистский мир — лекции по теории относительности, гравитации и космологии, 2010