Перпендикуля́рность — бинарное отношение между различными объектами (векторами, прямыми, подпространствами и т. д.).
Для обозначения перпендикулярности имеется общепринятый символ:⊥{displaystyle perp }, предложенный в 1634 году французским математиком Пьером Эригоном.Например, перпендикулярность прямых m{displaystyle m} и n{displaystyle n} записывают как m⊥n{displaystyle mperp n}.
Содержание
На плоскости
Перпендикулярные прямые на плоскости
Две прямые на плоскости называются перпендикулярными, если при пересечении образуют 4 прямых угла.
Про прямую m{displaystyle m}
перпендикулярную к прямой ℓ{displaystyle ell } проведённую через точку P{displaystyle P} вне прямой ℓ{displaystyle ell } , говорят, что m{displaystyle m} есть перпендикуляр опущенный из P{displaystyle P} на ℓ{displaystyle ell } .Если же точка P{displaystyle P} лежит на прямой ℓ{displaystyle ell } , то говорят, что m{displaystyle m} есть перпендикуляр к восстановленный из P{displaystyle P} к ℓ{displaystyle ell } (устаревший термин восставленный[1]).
В координатах
В аналитическом выражении прямые, заданные линейными функциями
- y=a⋅x+b{displaystyle y=acdot x+b}
и
- y=k⋅x+m{displaystyle y=kcdot x+m}
будут перпендикулярны, если выполнено следующее условие на их угловые коэффициенты
- a⋅k=−1.{displaystyle acdot k=-1.}
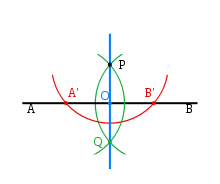
Построение перпендикуляра
‘Шаг 1: (красный) С помощью циркуля проведём полуокружность с центром в точке P, получив точки А’ и В.
‘Шаг 2: (зелёный) Не меняя радиуса, построим две полуокружности с центром в точках A’ и В соответственно, проходящими через точку P. Кроме точки P есть ещё одна точка пересечения этих полуокружностей, назовём её Q.
Шаг 3: (синий) Соединяем точки P и Q. PQ и есть перпендикуляр к прямой AB.
Координаты точки основания перпендикуляра к прямой
Пусть прямая задаётся точками A(xa,ya){displaystyle A(x_{a},y_{a})}
и B(xb,yb){displaystyle B(x_{b},y_{b})} . На прямую опускается перпендикуляр из точки P(xp,yp){displaystyle P(x_{p},y_{p})} .Тогда основание перпендикуляра O(xo,yo){displaystyle O(x_{o},y_{o})} можно найти следующим образом.
Если xa=xb{displaystyle x_{a}=x_{b}}
(вертикаль), то xo=xa{displaystyle x_{o}=x_{a}} и yo=yp{displaystyle y_{o}=y_{p}} .Если ya=yb{displaystyle y_{a}=y_{b}} (горизонталь), то xo=xp{displaystyle x_{o}=x_{p}} и yo=ya{displaystyle y_{o}=y_{a}} .
Во всех остальных случаях:
- xo=xa⋅(yb−ya)2+xp⋅(xb−xa)2+(xb−xa)⋅(yb−ya)⋅(yp−ya)(yb−ya)2+(xb−xa)2{displaystyle x_{o}={frac {x_{a}cdot (y_{b}-y_{a})^{2}+x_{p}cdot (x_{b}-x_{a})^{2}+(x_{b}-x_{a})cdot (y_{b}-y_{a})cdot (y_{p}-y_{a})}{(y_{b}-y_{a})^{2}+(x_{b}-x_{a})^{2}}}} ;
- yo=(xb−xa)⋅(xp−xo)(yb−ya)+yp{displaystyle y_{o}={frac {(x_{b}-x_{a})cdot (x_{p}-x_{o})}{(y_{b}-y_{a})}}+y_{p}} .
В трёхмерном пространстве
Перпендикулярные прямые
Две прямые в пространстве перпендикулярны друг другу, если они соответственно параллельны некоторым двум другим взаимно перпендикулярным прямым, лежащим в одной плоскости. Две прямые, лежащие в одной плоскости, называются перпендикулярными (или взаимно перпендикулярными), если они образуют четыре прямых угла.
Перпендикулярность прямой к плоскости
Определение: Прямая называется перпендикулярной к плоскости, если она перпендикулярна всем прямым, лежащим в этой плоскости.
Признак: Если прямая перпендикулярна двум пересекающимся прямым плоскости, то она перпендикулярна этой плоскости.
Плоскость, перпендикулярная одной из двух параллельных прямых, перпендикулярна и другой. Через любую точку пространства проходит прямая, перпендикулярная к данной плоскости, и притом только одна.
Перпендикулярные плоскости
Две плоскости называются перпендикулярными, если двугранный угол между ними равен 90°.
- Если плоскость проходит через прямую, перпендикулярную другой плоскости, то эти плоскости перпендикулярны.
- Если из точки, принадлежащей одной из двух перпендикулярных плоскостей, провести перпендикуляр к другой плоскости, то этот перпендикуляр полностью лежит в первой плоскости.
- Если в одной из двух перпендикулярных плоскостей провести перпендикуляр к их линии пересечения, то этот перпендикуляр будет перпендикулярен второй плоскости.
- Плоскость, перпендикулярная двум пересекающимся плоскостям, перпендикулярна их линии пересечения[2].
В многомерных пространствах
| В разделе не хватает ссылок на источники (см. рекомендации по поиску). Информация должна быть проверяема, иначе она может быть удалена. Вы можете отредактировать статью, добавив ссылки на авторитетные источники в виде сносок. (29 июля 2014) |
Перпендикулярность плоскостей в 4-мерном пространстве
Перпендикулярность плоскостей в четырёхмерном пространстве имеет два смысла: плоскости могут быть перпендикулярны в 3-мерном смысле, если они пересекаются по прямой (а следовательно, лежат в одной гиперплоскости), и двугранный угол между ними равен 90°.
Плоскости могут быть также перпендикулярны в 4-мерном смысле, если они пересекаются в точке (а следовательно, не лежат в одной гиперплоскости), и любые 2 прямые, проведённые в этих плоскостях через точку их пересечения (каждая прямая в своей плоскости), перпендикулярны.
В 4-мерном пространстве через данную точку можно провести ровно 2 взаимно перпендикулярные плоскости в 4-мерном смысле (поэтому 4-мерное евклидово пространство можно представить как декартово произведение двух плоскостей). Если же объединить оба вида перпендикулярности, то через данную точку можно провести 6 взаимно перпендикулярных плоскостей (перпендикулярных в любом из двух вышеупомянутых значений).
Существование шести взаимно перпендикулярных плоскостей можно пояснить таким примером. Пусть дана система декартовых координат x y z t. Для каждой пары координатных прямых существует плоскость, включающая эти две прямые. Количество таких пар равно (42)=6{displaystyle {tbinom {4}{2}}=6}
: xy, xz, xt, yz, yt, zt, и им соответствуют 6 плоскостей. Те из этих плоскостей, которые включают одноимённую ось, перпендикулярны в 3-мерном смысле и пересекаются по прямой (например, xy и xz, yz и zt), а те, которые не включают одноимённых осей, перпендикулярны в 4-мерном смысле и пересекаются в точке (например, xy и zt, yz и xt).
Перпендикулярность прямой и гиперплоскости
Пусть задано n-мерное евклидово пространство Rn{displaystyle mathbb {R} ^{n}}
(n>2) и ассоциированное с ним векторное пространство Wn{displaystyle W^{n}} , а прямая l с направляющим векторным пространством L1{displaystyle L^{1}} и гиперплоскость Πk{displaystyle Pi _{k}} с направляющим векторным пространством Lk{displaystyle L^{k}} (где L1⊂Wn{displaystyle L_{1}subset W^{n}} , Lk⊂Wn, k<n{displaystyle L^{k}subset W^{n}, k<n} ) принадлежат пространству Rn{displaystyle mathbb {R} ^{n}} .
Прямая l называется перпендикулярной гиперплоскости Πk{displaystyle Pi _{k}}
, если подпространство L1{displaystyle L_{1}} ортогонально подпространству Lk{displaystyle L^{k}} , то есть (∀a→∈L1) (∀b→∈Lk) a→b→=0{displaystyle (forall {vec {a}}in L_{1}) (forall {vec {b}}in L_{k}) {vec {a}}{vec {b}}=0}
См. также
Примечания
- ↑ А. П. Киселёв. Элементарная геометрия / под редакцией Н. А. Глаголева. — 1938.
- ↑ Александров А.Д., Вернер А. Л., Рыжик В.И. Стереометрия. Геометрия в пространстве. — Висагинас: Alfa, 1998. — С. 46. — 576 с. — (Библиотека школьника). — ISBN 9986582539.

 , предложенный в
, предложенный в  и n{displaystyle n}
и n{displaystyle n} записывают как m⊥n{displaystyle mperp n}
записывают как m⊥n{displaystyle mperp n} .
. проведённую через точку P{displaystyle P}
проведённую через точку P{displaystyle P} вне прямой ℓ{displaystyle ell }
вне прямой ℓ{displaystyle ell }


 и B(xb,yb){displaystyle B(x_{b},y_{b})}
и B(xb,yb){displaystyle B(x_{b},y_{b})} . На прямую опускается перпендикуляр из точки P(xp,yp){displaystyle P(x_{p},y_{p})}
. На прямую опускается перпендикуляр из точки P(xp,yp){displaystyle P(x_{p},y_{p})} .Тогда основание перпендикуляра O(xo,yo){displaystyle O(x_{o},y_{o})}
.Тогда основание перпендикуляра O(xo,yo){displaystyle O(x_{o},y_{o})} можно найти следующим образом.
можно найти следующим образом.  (вертикаль), то xo=xa{displaystyle x_{o}=x_{a}}
(вертикаль), то xo=xa{displaystyle x_{o}=x_{a}} и yo=yp{displaystyle y_{o}=y_{p}}
и yo=yp{displaystyle y_{o}=y_{p}} .Если ya=yb{displaystyle y_{a}=y_{b}}
.Если ya=yb{displaystyle y_{a}=y_{b}} (горизонталь), то xo=xp{displaystyle x_{o}=x_{p}}
(горизонталь), то xo=xp{displaystyle x_{o}=x_{p}} и yo=ya{displaystyle y_{o}=y_{a}}
и yo=ya{displaystyle y_{o}=y_{a}} .
. ;
; .
. : xy, xz, xt, yz, yt, zt, и им соответствуют 6 плоскостей. Те из этих плоскостей, которые включают одноимённую ось, перпендикулярны в 3-мерном смысле и пересекаются по прямой (например, xy и xz, yz и zt), а те, которые не включают одноимённых осей, перпендикулярны в 4-мерном смысле и пересекаются в точке (например, xy и zt, yz и xt).
: xy, xz, xt, yz, yt, zt, и им соответствуют 6 плоскостей. Те из этих плоскостей, которые включают одноимённую ось, перпендикулярны в 3-мерном смысле и пересекаются по прямой (например, xy и xz, yz и zt), а те, которые не включают одноимённых осей, перпендикулярны в 4-мерном смысле и пересекаются в точке (например, xy и zt, yz и xt). (n>2) и ассоциированное с ним векторное пространство Wn{displaystyle W^{n}}
(n>2) и ассоциированное с ним векторное пространство Wn{displaystyle W^{n}} , а прямая l с направляющим векторным пространством L1{displaystyle L^{1}}
, а прямая l с направляющим векторным пространством L1{displaystyle L^{1}} и
и  с направляющим векторным пространством Lk{displaystyle L^{k}}
с направляющим векторным пространством Lk{displaystyle L^{k}} (где L1⊂Wn{displaystyle L_{1}subset W^{n}}
(где L1⊂Wn{displaystyle L_{1}subset W^{n}} , Lk⊂Wn, k<n{displaystyle L^{k}subset W^{n}, k<n}
, Lk⊂Wn, k<n{displaystyle L^{k}subset W^{n}, k<n} ) принадлежат пространству Rn{displaystyle mathbb {R} ^{n}}
) принадлежат пространству Rn{displaystyle mathbb {R} ^{n}} ортогонально подпространству Lk{displaystyle L^{k}}
ортогонально подпространству Lk{displaystyle L^{k}}
