Цилиндрической системой координат называют трёхмерную систему координат, являющуюся расширением полярной системы координат путём добавления третьей координаты (обычно обозначаемой z{displaystyle z}), которая задаёт высоту точки над плоскостью.
 Точка в цилиндрических координатах.
Точка в цилиндрических координатах.
Точка P{displaystyle P} даётся как (ρ,φ,z){displaystyle (rho ,;varphi ,;z)}. В терминах прямоугольной системы координат:
- ρ⩾0{displaystyle rho geqslant 0} — расстояние от O{displaystyle O} до P′{displaystyle P’}, ортогональной проекции точки P{displaystyle P} на плоскость XY{displaystyle XY}. Или то же самое, что расстояние от P{displaystyle P} до оси Z{displaystyle Z}.
- 0⩽φ <360∘{displaystyle 0leqslant varphi <360^{circ }} — угол между осью X{displaystyle X} и отрезком OP′{displaystyle OP’}.
- z{displaystyle z} равна аппликате точки P{displaystyle P}.
При использовании в физических науках и технике международный стандарт ISO 31-11 рекомендует использовать обозначения (ρ,φ,z){displaystyle (rho ,;varphi ,;z)}.
Некоторые математики используют (r,θ,z){displaystyle (r,;theta ,;z)}.
Цилиндрические координаты удобны при анализе поверхностей, симметричных относительно какой-либо оси, если ось Z{displaystyle Z} взять в качестве оси симметрии. Например, бесконечно длинный круглый цилиндр в прямоугольных координатах имеет уравнение x2+y2=c2{displaystyle x^{2}+y^{2}=c^{2}}, а в цилиндрических — очень простое уравнение ρ=c{displaystyle rho =c}. Отсюда и идёт для данной системы координат имя «цилиндрическая».
Содержание
Переход к другим системам координат
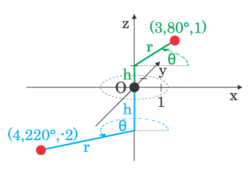 2 точки в цилиндрических координатах.
2 точки в цилиндрических координатах.
Поскольку цилиндрическая система координат — только одна из многих трёхмерных систем координат, существуют законы преобразования координат между цилиндрической системой координат и другими системами.
Декартова система координат
Основная статья: Прямоугольная система координат
Закон преобразования координат от декартовых к цилиндрическим:
- {x=ρcosφ,y=ρsinφ,z=z.{displaystyle {begin{cases}x=rho cos varphi ,\y=rho sin varphi ,\z=z.end{cases}}}
Закон преобразования координат от цилиндрических к декартовым:
- {ρ=x2+y2,φ=arctg(yx),z=z.{displaystyle {begin{cases}rho ={sqrt {x^{2}+y^{2}}},\varphi =mathrm {arctg} left({dfrac {y}{x}}right),\z=z.end{cases}}}
Якобиан равен:
- J=ρ.{displaystyle J=rho .}
Дифференциальные характеристики
Цилиндрические координаты являются ортогональными, поэтому метрический тензор имеет в них диагональный вид:
- gij=(1000ρ20001),gij=(10001/ρ20001).{displaystyle g_{ij}={begin{pmatrix}1&0&0\0&rho ^{2}&0\0&0&1end{pmatrix}},quad g^{ij}={begin{pmatrix}1&0&0\0&1/rho ^{2}&0\0&0&1end{pmatrix}}.}
- Квадрат дифференциала длины кривой
- ds2=dρ2+ρ2dφ2+dz2.{displaystyle ds^{2}=drho ^{2}+rho ^{2},dvarphi ^{2}+dz^{2}.}
- Коэффициенты Ламэ имеют вид:
- Hρ=1,Hφ=ρ,Hz=1.{displaystyle H_{rho }=1,quad H_{varphi }=rho ,quad H_{z}=1.}
- Символы Кристоффеля {r,φ,z}{displaystyle {r,;varphi ,;z}} :
- Γ221=−r,Γ212=Γ122=1r.{displaystyle Gamma _{22}^{1}=-r,quad Gamma _{21}^{2}=Gamma _{12}^{2}={frac {1}{r}}.} Остальные равны нулю.
См. также
| В статье не хватает ссылок на источники (см. также рекомендации по поиску). Информация должна быть проверяема, иначе она может быть удалена. Вы можете отредактировать статью, добавив ссылки на авторитетные источники в виде сносок. |

 ), которая задаёт высоту точки над плоскостью.
), которая задаёт высоту точки над плоскостью. даётся как (ρ,φ,z){displaystyle (rho ,;varphi ,;z)}
даётся как (ρ,φ,z){displaystyle (rho ,;varphi ,;z)} . В терминах
. В терминах  — расстояние от O{displaystyle O}
— расстояние от O{displaystyle O} до P′{displaystyle P’}
до P′{displaystyle P’} , ортогональной проекции точки P{displaystyle P}
, ортогональной проекции точки P{displaystyle P} . Или то же самое, что расстояние от P{displaystyle P}
. Или то же самое, что расстояние от P{displaystyle P} .
. — угол между осью X{displaystyle X}
— угол между осью X{displaystyle X} и отрезком OP′{displaystyle OP’}
и отрезком OP′{displaystyle OP’} .
. , а в цилиндрических — очень простое уравнение ρ=c{displaystyle rho =c}
, а в цилиндрических — очень простое уравнение ρ=c{displaystyle rho =c} . Отсюда и идёт для данной системы координат имя «цилиндрическая».
. Отсюда и идёт для данной системы координат имя «цилиндрическая».





 :
: Остальные равны нулю.
Остальные равны нулю.