Лине́йная а́лгебра — раздел алгебры, изучающий объекты линейной природы: векторные (или линейные) пространства, линейные отображения[⇨], системы линейных уравнений[⇨], среди основных инструментов, используемых в линейной алгебре — определители, матрицы[⇨], сопряжение. Теория инвариантов?! и тензорное исчисление обычно (в целом или частично) также считаются составными частями линейной алгебры[1]. Такие объекты как квадратичные и билинейные формы[⇨], тензоры[⇨] и операции как тензорное произведение непосредственно вытекают из изучения линейных пространств, но как таковые относятся к полилинейной алгебре.
Линейная алгебра обобщена средствами общей алгебры, в частности, современное определение линейного (векторного) пространства[⇨] опирается исключительно на абстрактные структуры, а многие результаты линейной алгебры обобщены на произвольные модули над кольцом. Более того, методы линейной алгебры широко используются и в других разделах общей алгебры, в частности, нередко применяется такой приём, как сведение абстрактных структур к линейным и изучение их относительно простыми и хорошо проработанными средствами линейной алгебры, так, например, реализуется в теории представлений групп[⇨]. Функциональный анализ возник как применение методов математического анализа и линейной алгебры к бесконечномерным линейным пространствам, и во многом базируется на методах линейной алгебры и в дальнейших своих обобщениях. Также линейная алгебра нашла широкое применение в многочисленных приложениях (в том числе, в линейном программировании[⇨], в эконометрике[⇨]) и естественных науках (например, в квантовой механике[⇨]).
Содержание
История
Первые элементы линейной алгебры следовали из практических вычислительных задач вокруг решения линейных уравнений, в частности, такие арифметические приёмы как тройное правило[en]* и правило ложного положения?! были сформулированы ещё в древности. В «Началах» Евклида фигурируют две теории «линейного» характера: теория величины и теория целых чисел. Близкие к современным матричным методам подходы к решению систем линейных уравнений обнаруживаются у вавилонян (системы из двух уравнений с двумя переменными) и древних китайцев (в «Математике в девяти книгах», до трёх уравнений с тремя переменными)[2]. Однако после достижения определённости с основными вопросами нахождения решений систем линейных уравнений развитие раздела практически не происходило, и даже в конце XVIII — начале XIX века считалось, что проблем относительно уравнений первой степени больше не существует, притом системы линейных уравнений с числом переменных, отличающихся от количества уравнений или с линейно-зависимыми коэффициентами в левой части попросту считались некорректными[3].
Методы, сформировавшие линейную алгебру как самостоятельную отрасль математики, уходят корнями в другие разделы. Ферма в 1630-е годы, создав классификацию плоских кривых, ввёл в математику (ключевой для линейной алгебры) принцип размерности и разделил задачи аналитической геометрии по числу неизвестных (с одним неизвестным — отыскание точки, с двумя — кривой или геометрического места на плоскости, с тремя — поверхности). Эйлер создал классификацию кривых по порядкам обратив внимание на линейный характер преобразований координат, ввёл в оборот понятие аффинного преобразования (и само слово «аффинность»)[4].
Первое введение понятия определителя для целей решения систем линейных уравнений относят к Лейбницу (1678[5] или 1693 год[6]), но эти работы не были опубликованы. Также определитель обнаруживается в трудах Сэки Такакадзу 1683 года, в которых он обобщил метод решения систем линейных уравнений из древнекитайской «Математики в девяти книгах» до n{displaystyle n}
уравнений с n{displaystyle n} неизвестными[7]. Маклорен, фактически используя простейшие определители в трактате вышедшем 1748 году приводит решения систем из двух линейных уравнений с двумя неизвестными и трёх уравнений с тремя неизвестными[8]. Крамер и Безу в работах по проблеме отыскания плоской кривой, проходящей через заданную точку, вновь построили это понятие (правило Крамера сформулировано в 1750 году), Вандермонд и Лагранж дали индуктивное определение для случаев n>3{displaystyle n>3} [9], а целостное определение и окончательные свойства определителей дали Коши (1815) и Якоби (1840-е годы)[3]. Гауссу (около 1800 года) принадлежит формализация метода последовательного исключения переменных для решения этих задач, ставшего известным под его именем[10] (хотя по существу для решения систем линейных уравнений именно этот метод и использовался с древности[4]).
Д’Аламбер, Лагранж и Эйлер, работая над теорией дифференциальных уравнений в том или ином виде выделили класс линейных однородных уравнений и установили факт, что общее решение такого уравнения порядка n{displaystyle n}
является линейной комбинацией n{displaystyle n} частных решений (однако, при этом не отмечали необходимость линейной независимости решений)[11]. Основываясь на наблюдении, что множество значений целочисленной функции f(x,y){displaystyle f(x,y)} не меняется от того, что над x{displaystyle x} и y{displaystyle y} совершается линейная подстановка (с целыми коэффициентами и определителем, равным 1), Лагранж в 1769 году разрабатывает теорию представления целых чисел квадратичными формами, а в 1770 году обобщает теорию до алгебраических форм. Гаусс развил теорию Лагранжа, рассматривая вопросы эквивалентности форм, и ввёл серию понятий, относящихся к линейным подстановкам, самым важным из которых было понятие сопряжённой (транспонированной) подстановки[12]. С этого времени арифметические и алгебраические исследования квадратичных и связанных с ними билинейных форм составляют существенную часть предмета линейной алгебры[13].
Ещё одним источником подходов для линейной алгебры стала проективная геометрия, создание которой начато Дезаргом в XVII веке и получившей значительное развитие в трудах Монжа конца XVIII века и в дальнейшем в работах Понселе, Брианшона и Шаля начала — середины XIX века. В те времена основным предметом изучения проективной геометрии были коники и квадрики, являющиеся по сути квадратичными формами. Кроме того, понятие двойственности проективных пространств, введённое Монжем, являет один из аспектов двойственности в линейных пространствах (однако эта связь была замечена только в конце XIX века Пинкерле?!).[14]
Но основной базой линейной алгебры стало фактически влившееся в раздел векторное исчисление, очерченное Гауссом в работах по геометрической интерпретации комплексных чисел (1831) и обретшее окончательную форму в трудах Мёбиуса, Грассмана и Гамильтона 1840-х — 1850-х годах. Так, Гамильтон в 1843 году обобщает комплексные числа до кватернионов и даёт им геометрическую интерпретацию по аналогии с гауссовой (Гамильтону, в том числе, принадлежит и введение термина «вектор»), а в 1844 году Грассман строит понятие внешней алгебры, описывающей подпространства линейного пространства[15]. Всеобщее признание векторного исчисления в конце XIX века существенно связано с применением векторов ведущими физиками-теоретиками того времени, прежде всего, Максвеллом, Гиббсом, Хевисайдом, в частности, физиками тщательно проработана векторная алгебра в трёхмерном евклидовом пространстве: введены понятия скалярного, векторного и смешанного произведений векторов, набла-оператор[16], сформирована вошедшая в традицию символика, также начиная с этого времени векторы проникают и в школьные программы.
Понятие матрицы ввёл Сильвестр в 1850 году[17][18]. Кэли обстоятельно разрабатывает матричное исчисление, публикуя в 1858 году «Мемуар о теории матриц» (англ. Memoir on the theory of matrices), принципиально, что Кэли рассматривает матрицы как нотацию для линейных подстановок[15]. В частности, в этой работе Кэли вводит сложение и умножение матриц, обращение матриц, рассматривает характеристические многочлены матриц и формулирует и доказывает для случаев 2×2 и 3×3 утверждение об обращении в нуль характеристического многочлена квадратной матрицы (известное как теорема Гамильтона — Кэли, так как случай 4×4 доказал Гамильтон с использованием кватернионов), доказательство для общего случая принадлежит Фробениусу (1898). Системы линейных уравнений в матрично-векторном виде впервые появились, по-видимому, в работах Лагерра (1867).
Теория инвариантов?! в классическом варианте — учение о свойствах алгебраических форм, сохраняющихся при линейных преобразованиях, сформирована начиная с 1840-х годов в работах Кэли, Эрмита и Сильвестра (известных как «инвариантная троица», фр. la trinité invariantive), считается[19], что именно теория инвариантов и приводит к созданию принципов решения произвольных систем линейных уравнений. В частности, Эрмит[уточнить] сформулировал и решил в частном случае проблему нахождения системы линейных диофантовых уравнений, решение в общем случае найдено Смитом?! (англ. Henry John Stephen Smith), результат которого остался незамеченным, пока не был обнаружен в 1878 году Фробениусом[19]. Финальный вид результаты о системах линейных уравнений с произвольными числовыми коэффициентами получили в работах, организованных Кронекером, в которых принимали участие Вейерштрасс, Фробениус и группа немецких учёных, особое внимание уделялось строгости и точности формулировок. В частности, определитель в курсе лекций Кронекера — Вейршртаса вводился как полилинейная знакопеременная функция от n{displaystyle n}
векторов n{displaystyle n} -мерного пространства, нормированная таким образом, что принимает значение 1 для единичной матрицы; притом это определение эквивалентно вытекающему из исчисления Грассмана[19][20]. Фробениус в 1877 году ввёл понятие ранга матрицы, основываясь на котором в ближайшие годы сразу несколько учёных доказали утверждение об эквивалентности разрешимости системы линейных уравнений совпадением рангов её основной и расширенной матрицы, известной в русских и польских источниках как теорема Кронекера — Капелли, во французских — теорема Руше (фр. Eugène Rouché) — Фонтене (фр. Georges Fontené), в немецких и испанских — теорема Руше — Фробениуса, в итальянских и английских — теорема Руше — Капелли.
В 1888 году Пеано на базе исчисления Грассмана впервые в явном виде сформулировал аксиомы линейного пространства (векторных пространств над полем действительных чисел в том числе бесконечномерных) и применил обозначения, сохранившиеся в употреблении в XX—XXI века[21]. Тёплиц в начале 1910-х годов обнаружил, что при помощи аксиоматизации линейного пространства для доказательства основных теорем линейной алгебры не требуется прибегать к понятию определителя, что позволяет распространить их результаты на случай бесконечного числа измерений, иными словами, линейная алгебра применима при любом основном поле[21]. Аксиоматическое определение векторного и евклидова пространства было впервые чётко сформулировано в начале XX века практически одновременно Вейлем и фон Нейманом, исходя из запросов квантовой механики[22].
Тензорное исчисление, разработанное в 1890-е годы Риччи и Леви-Чивитой, составило своей алгебраической частью основное содержание полилинейной алгебры. Особое внимание к этому подразделу было привлечено в 1910-е — 1930-е годы благодаря широкому использованию тензоров Эйнштейном и Гильбертом в математическом описании общей теории относительности.
В 1922 году Банах, изучая полные нормированные линейные пространства, ставшие известными после его работ как банаховы, обнаружил, что уже в конечном случае возникают линейные пространства, не изоморфные своему сопряжению[21], и в этой связи в первой половине XX века методы и результаты линейной алгебры обогатили функциональный анализ, сформировав его основной предмет в современном понимании — изучение топологических линейных пространств[23]. Также в 1920-е — 1950-е годы получает распространение направление по линеаризации общей алгебры, так, развивая результат Дедекинда о линейной независимости любых автоморфизмов поля, Артин линеаризовывает теорию Галуа, а в 1950-е годы, прежде всего, в работах Джекобсона, эти результаты обобщены на произвольные расширения тел[24]; благодаря этим построениям обретена возможность применения инструментов и достижений хорошо изученной линейной алгебры в весьма абстрактных разделах общей алгебры.
Со второй половины XX века с появлением компьютеров, развитием методов вычислительной математики и компьютерной алгебры в рамках линейной алгебры получило бурное развитие вычислительное направление — отыскание методов и алгоритмов, обеспечивающих эффективное решение задач линейной алгебры с использованием вычислительной техники, сформировался самостоятельный раздел вычислительной линейной алгебры (англ. numerical linear algebra), а решение задач линейной алгебры стало одной из важных практических составляющих использования компьютеров. В числе работ, положивших начало разработке этого направления, стало создание Тьюрингом алгоритма LU-разложения квадратной матрицы на верхнюю и нижнюю треугольные (1948)[25]. Показательно, что результаты тестов Linpack[en], в которых вычислительные системы должны решить сложные системы линейных уравнений с использованием LU-разложения, считаются основным показателем производительности вычислений с плавающей запятой, в том числе и для кластерных систем. В 1950-е — 1960-е годы крупные исследования в области вычислительной линейной алгебры опубликованы Фаддеевым и Уикинсоном, значительные результаты в 1970-е — 2000-е годы получены Марчуком, Самарским, Годуновым, Голубом (англ. Gene H. Golub), Аксельсоном[26].
Основные конструкции
Матрицы и определители
Основные статьи: Определитель и Матрица (математика)
Матрица — математический объект, записываемый в прямоугольной таблице размером m×n{displaystyle mtimes n}
, в ячейках которой расположены элементы произвольного заранее выбранного (основного) поля (в наиболее общем случае — ассоциативного кольца[27]) — это могут быть целые, вещественные или комплексные числа, векторы, рациональные функции — в зависимости от приложений и задач:
- (a11⋯a1j⋯a1n⋮⋱⋮⋱⋮ai1⋯aij⋯ain⋮⋱⋮⋱⋮am1⋯amj⋯amn){displaystyle {begin{pmatrix}a_{11}&cdots &a_{1j}&cdots &a_{1n}vdots &ddots &vdots &ddots &vdots a_{i1}&cdots &a_{ij}&cdots &a_{in}vdots &ddots &vdots &ddots &vdots a_{m1}&cdots &a_{mj}&cdots &a_{mn}end{pmatrix}}}
Для матриц используется также сокращённая запись (aij){displaystyle (a_{ij})}
, но обычно с матрицами оперируют как с едиными объектами: над матрицами определены сложение и умножение, также матрицу можно умножить на скаляр — элемент основного поля, относительно этих операций образуют векторное пространство[⇨] над основным полем (или, в наиболее общем случае — модуль над кольцом). Другие операции над матрицами — транспонирование (замена строк на столбцы) и псевдообращение (обобщение обращения квадратных матриц). Матрицы размера 1×n{displaystyle 1times n} и m×1{displaystyle mtimes 1} называются вектор-строка и вектор-столбец соответственно.
Матрица с равным числом строк и столбцов называется квадратной, в зависимости от содержания они могут быть диагональными (все элементы — нули основного поля, кроме диагональных: i≠j⇒aij=0{displaystyle ineq jRightarrow a_{ij}=0}
), единичными (все диагональные элементы равны единице основного поля, а остальные — нулю), симметричными (все элементы симметричны относительно главной диагонали: aij=aji{displaystyle a_{ij}=a_{ji}} ), кососимметричными (aij=−aji{displaystyle a_{ij}=-a_{ji}} ), треугольными (все элементы выше или ниже главной диагонали равны нулю), ортогональными. Среди квадратных матриц вводится отношение подобия (A∼B⇔∃P(A=P−1⋅B⋅P{displaystyle Asim BLeftrightarrow exists P(A=P^{-1}cdot Bcdot P} ), где P−1{displaystyle P^{-1}} — матрица, обратная P{displaystyle P} ), такие характеристики матриц, как ранг (максимальное количество линейно независимых строк или столбцов) и характеристический многочлен инвариантны относительно подобия[28]. Также одинаковы для подобных прямоугольных матриц такие характеристики, как след (взятие суммы элементов главной диагонали) и определитель.
Определитель — многочлен, комбинирующий элементы прямоугольной матрицы особым способом, благодаря которому независимо от транспонирования и линейных комбинаций строк или столбцов характеризуется содержание матрицы; в частности, если в матрице есть линейно-зависимые строки или столбцы — определитель равен нулю. Квадратные матрицы, определитель которых равен нулю называются вырожденными, для них не определено обращение; если определитель отличен от нуля — то матрица называется невырожденной. Определитель играет ключевую роль в решении систем линейных уравнений в общем виде, на его базе вводятся понятия минора, дополнительного минора, алгебраического дополнения[29].
Векторы
Основная статья: Векторное исчисление
Понятие вектора (сам термин «вектор» был введен У. Гамильтоном) изначально возникло как геометрическая абстракция для объектов, характеризующихся одновременно величиной и направлением, таких как скорость, момент силы, напряжённость электрического поля, намагниченность. В начале XX века изначальная интерпретация векторов (до сих пор используемая в элементарной математике) как «направленных отрезков» сменилось на аксиоматику векторного пространства с двумя операциямиː сложением векторов и умножение вектора на числа (более общо, на элементы поля). Кроме того, часто вводятся различные виды произведения векторов: скалярное, векторное, смешанное, псевдоскалярное, двойное векторное.
Ключевую роль в линейной алгебре играет понятие линейной независимости векторов, которое лежит в основе определений базиса и размерности векторного пространстваː число n{displaystyle n}
называется размерностью векторного пространства, если оно содержит n{displaystyle n} линейно независимых векторов и любые k>n{displaystyle k>n} векторов этого пространства являются линейно зависимыми. Такое векторное пространство называется n{displaystyle n} -мерным, и любой его вектор представляется упорядоченной последовательностью n{displaystyle n} чисел (однозначно определяемых при выборе какого-либо базиса). Таким образом, векторы могут быть записаны в виде матриц размера 1×n{displaystyle 1times n} или n×1{displaystyle ntimes 1} — векторов-столбцов и векторов-строк соответственно, а все операции векторной алгебры могут быть сведены к алгебре матрицː например, сложение векторов совпадает со сложением матриц, а векторное умножение векторов может быть выражено как произведение кососимметрической матрицы, построенной из первого сомножителя и вектора-стоблца, представляющего второй сомножитель.
Тензоры
Основная статья: Тензорное исчисление
Тензоры возникли как естественное развитие представлений об объектах линейной алгебры: если скаляр в n{displaystyle n}
-мерном представляется нульмерным объектом (состоящим только из одного элемента поля), вектор — одномерным массивом (матрицей размера 1×n{displaystyle 1times n} ), линейное преобразование — двумерной матрицей, то тензор может быть представлен как многомерный массив элементов поля размера n×n×⋯×n{displaystyle ntimes ntimes cdots times n} (количество измерений массива называют валентностью тензора), а скаляры, векторы, линейные операторы оказываются частными случаями тензора (с валентностями 0, 1 и 2 соответственно). Следующее обобщение, использованное в понятии тензора взято из возможности представления линейного функционала как ковектора и идея двойственности между пространством и его сопряжением — пространством его линейных функционалов; используя эту возможность, тензор валентности r{displaystyle r} рассматривается как l{displaystyle l} раз контравариантный, то есть, рассматриваемый соответствующими компонентами в «обычном» базисе, и k{displaystyle k} раз ковариантный, то есть, с компонентами в сопряжённом пространстве (r=k+l{displaystyle r=k+l} , «тензор ранга (l,k){displaystyle (l,k)} »).
В тензорной алгебре вводятся и изучаются линейные операции над тензорами, такие, как умножение на скаляр, сложение, свёртка. Особую роль играет операция тензорного произведения (⊗{displaystyle otimes }
), обобщение которой на линейные пространства позволило обобщить и определение тензора: рассматривать тензор ранга (l,k){displaystyle (l,k)} в линейном пространстве V{displaystyle V} как элемент тензорного произведения k{displaystyle k} экземпляров V{displaystyle V} и l{displaystyle l} экземпляров сопряжённого ему V∗{displaystyle V^{*}} :
- V⊗…⊗V⏟⊗V∗⊗…⊗V∗⏟kl{displaystyle {begin{matrix}underbrace {Votimes ldots otimes V} &otimes &underbrace {V^{*}otimes ldots otimes V^{*}} k&&lend{matrix}}} .
Квадратичные и билинейные формы
Основные статьи: Квадратичная форма и Билинейная форма
Алгебраические формы (однородные многочлены на векторных пространствах, задаваемые однородными многочленами от координат вектора) относятся к полилинейной алгебре, но квадратичные, билинейные формы, и некоторые специальные виды форм (полуторалинейные, эрмитовы) важны также в чисто линейной алгебре. Значение билинейных и квадратичных форм заключается в том, что они выражаются матрицами, как и линейные операторы.Наиболее детально изучены свойства симметричных (B(x,y)=B(y,x)){displaystyle (B(x,y)=B(y,x))}
и кососимметричных (B(x,y)=−B(y,x)){displaystyle (B(x,y)=-B(y,x))} билинейных форм.
Векторные пространства
Основная статья: Векторное пространство
Все математические структуры, изучаемые в линейной алгебре — векторы, тензоры, матрицы, алгебраические формы, а также операции над ними, универсализированы в общеалгебраическом понятии векторного (линейного) пространства. Векторное пространство ⟨V,F,+,⋅⟩{displaystyle langle V,{mathfrak {F}},+,cdot rangle }
определяется как алгебра над произвольным множеством элементов V{displaystyle V} , называемых векторами, и произвольным полем F{displaystyle {mathfrak {F}}} , элементы которого называются скалярами, притом векторы с операцией сложения векторов ⟨V,+⟩{displaystyle langle V,+rangle } образуют абелеву группу, и определена операция умножения векторов на скаляр: ⋅:F×V→V{displaystyle cdot :{mathfrak {F}}times Vto V} такая, что выполнены следующие свойства (1,α,β∈F,v,u∈V{displaystyle 1,alpha ,beta in {mathfrak {F}},,mathbf {v} ,mathbf {u} in V} ):
- 1⋅v=v{displaystyle 1cdot mathbf {v} =mathbf {v} } ,
- α⋅(v+u)=α⋅v+α⋅u{displaystyle alpha cdot (mathbf {v} +mathbf {u} )=alpha cdot mathbf {v} +alpha cdot mathbf {u} } ,
- (α+β)⋅v=α⋅v+β⋅v{displaystyle (alpha +beta )cdot mathbf {v} =alpha cdot mathbf {v} +beta cdot mathbf {v} } ,
- (αβ)⋅v=α⋅(β⋅v){displaystyle (alpha beta )cdot mathbf {v} =alpha cdot (beta cdot mathbf {v} )} .
В качестве поля иногда специально рассматриваются поле вещественных чисел (тогда говорят о вещественном векторном пространстве) или поле комплексных чисел (комплексное векторное пространство) с обычными операциями сложения и умножения, в частности, в теории выпуклых множеств многие результаты формулируются именно для вещественных или комплексных векторных пространств[30]. Но значительная часть утверждений и большинство конструкций действенны для произвольных полей, более того, многие результаты линейной алгебры, полученные для векторных пространств, в XX веке обобщены до унитарных модулей над некоммутативными телами и даже для произвольных модулей над кольцами или модулей с определёнными ограничениями.
Линейные комбинации векторов — конечные суммы вида α1v1+⋯+αnvn{displaystyle alpha _{1}mathbf {v} _{1}+dots +alpha _{n}mathbf {v} _{n}}
, для совокупности векторов вводится линейной независимости (если существует нетривиальная линейная комбинация, обращающаяся в нуль абелевой группы пространства), вводится понятие базиса как максимальной линейно-независимой совокупности, показывается, что мощность базиса (называемая размерностью векторного пространства) не зависит от его выбора.
Дальнейшие обобщения векторных пространств, такие, как наделение их полунормами, нормами, метриками, топологиями, изучаются в функциональном анализе.
Линейные отображения
Основная статья: Линейное отображение
Подобно теориям других алгебраических структур, линейная алгебра изучает отображения между векторными пространствами, которые сохраняют структуру векторного пространства. Линейное отображение (линейное преобразование, линейный оператор) произвольных векторных пространств над одним полем L:V→U{displaystyle L:Vto U}
— отображение, сохраняющее линейность:
- L(v1+v2)=L(v1)+L(v2){displaystyle L(mathbf {v} _{1}+mathbf {v} _{2})=L(mathbf {v} _{1})+L(mathbf {v} _{2})} ,
- L(α⋅v)=α⋅L(v){displaystyle L(alpha cdot mathbf {v} )=alpha cdot L(mathbf {v} )} .
Когда между двумя векторными пространствами существует взаимно-однозначное отображение, являющееся линейным, то эти пространства называются изоморфными; многие свойства векторных пространств сохраняются при изоморфных преобразованиях (инвариантны относительно изоморфизма).
Над классом всех линейных отображений данных векторных пространств можно определить структуру векторного пространства. Линейные отображения конечномерных векторных пространств могут быть записаны в матричной форме и их свойства уже изучаются средствами матриц[⇨].
Собственные векторы и собственные числа
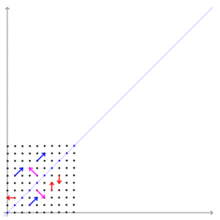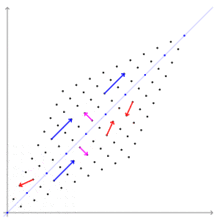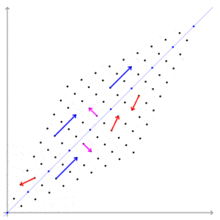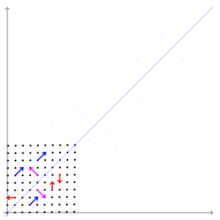 Синие и сиреневые векторы, сохраняющие направление при линейном преобразовании — собственные, красные — нетОсновная статья: Собственный вектор
Синие и сиреневые векторы, сохраняющие направление при линейном преобразовании — собственные, красные — нетОсновная статья: Собственный вектор
В общем случае действие линейных отображений может быть довольно сложным. Важной и распространённой задачей является нахождение такого базиса векторного пространства V{displaystyle V}
, в котором матрица данного линейного отображения L:V→V{displaystyle L:Vrightarrow V} имеет наиболее простой вид. При решении этой задачи ключевую роль играют инвариантные подпространства линейного отображения L{displaystyle L} — подпространства, образ которых при отображении L{displaystyle L} вложен в себя. Если найдены инвариантные подпространства ненулевой размерности W1,…,Wk{displaystyle W_{1},ldots ,W_{k}} (то есть, выполнено L(Wi)⊂Wi{displaystyle L(W_{i})subset W_{i}} ), прямая сумма которых составляет всё пространство V{displaystyle V} , то матрица отображения L{displaystyle L} имеет блочно-диагональный вид с блоками порядков n1,…,nk{displaystyle n_{1},ldots ,n_{k}} , ni=dimWi{displaystyle n_{i}=dim W_{i}} , на главной диагонали, если выбрать базис состоящим из k{displaystyle k} групп векторов, где i{displaystyle i} -ая группа является базисом в подпространстве Wi{displaystyle W_{i}} .
Простейшим случаем инвариантного подпространства является одномерное инвариантное подпространство W{displaystyle W}
, которое можно задать с помощью одного (любого) ненулевого вектора x∈W{displaystyle xin W} . В этом случае условие вложенности образа подпространства в себя принимает вид L(x)=λx{displaystyle L(x){=}lambda x} с некоторым числом λ{displaystyle lambda } ; такая конструкция приводит к определению собственного вектора и собственного числа: если для некоторого вектора x≠0{displaystyle xneq 0} и числа λ{displaystyle lambda } выполнено равенство L(x)=λx{displaystyle L(x){=}lambda x} , то λ{displaystyle lambda } называется собственным числом отображения L{displaystyle L} , а вектор x{displaystyle x} называется его собственным вектором. Собственные числа линейного отображения определены однозначно, а собственные векторы — с точностью до пропорциональности, то есть до умножения на произвольное ненулевое число.
В случае, если отображение имеет набор n{displaystyle n}
линейно независимых собственных векторов, число которых n{displaystyle n} равно размерности пространства V{displaystyle V} , из них можно составить базис (называемый собственным базисом данного отображения), в котором матрица отображения диагональна, при этом на главной диагонали стоят собственные числа. Такие линейные отображения называются диагонализируемыми. Достаточным (но не необходимым) условием диагонализируемости является наличие n{displaystyle n} различных собственных чисел.
Жорданова нормальная форма
Основная статья: Жорданова матрица
| Этот раздел статьи ещё не написан. Здесь может располагаться отдельный раздел. Помогите Википедии, написав его. (31 октября 2016) |
Применение
Решение систем линейных алгебраических уравнений
Основная статья: Система линейных алгебраических уравнений Система линейных уравнений от трёх переменных определяет набор плоскостей. Точка пересечения является решением.
Система линейных уравнений от трёх переменных определяет набор плоскостей. Точка пересечения является решением.
Система m линейных алгебраических уравнений с n неизвестными — это система уравнений вида
- {a11x1+a12x2+⋯+a1nxn=b1a21x1+a22x2+⋯+a2nxn=b2…am1x1+am2x2+⋯+amnxn=bm{displaystyle {begin{cases}a_{11}x_{1}+a_{12}x_{2}+dots +a_{1n}x_{n}=b_{1}a_{21}x_{1}+a_{22}x_{2}+dots +a_{2n}x_{n}=b_{2}dots a_{m1}x_{1}+a_{m2}x_{2}+dots +a_{mn}x_{n}=b_{m}end{cases}}}
Она может быть представлена в матричной форме как:
- (a11a12⋯a1na21a22⋯a2n⋮⋮⋱⋮am1am2⋯amn)(x1x2⋮xn)=(b1b2⋮bm){displaystyle {begin{pmatrix}a_{11}&a_{12}&cdots &a_{1n}a_{21}&a_{22}&cdots &a_{2n}vdots &vdots &ddots &vdots a_{m1}&a_{m2}&cdots &a_{mn}end{pmatrix}}{begin{pmatrix}x_{1}x_{2}vdots x_{n}end{pmatrix}}={begin{pmatrix}b_{1}b_{2}vdots b_{m}end{pmatrix}}}
или:
- Ax=b{displaystyle Ax=b} .
| Этот раздел не завершён. Вы поможете проекту, исправив и дополнив его. |
Теория представлений
| Этот раздел статьи ещё не написан. Здесь может располагаться отдельный раздел. Помогите Википедии, написав его. (31 октября 2016) |
Линейное программирование
Основная статья: Линейное программирование
| Этот раздел статьи ещё не написан. Здесь может располагаться отдельный раздел. Помогите Википедии, написав его. (31 октября 2016) |
Эконометрика
| Этот раздел статьи ещё не написан. Здесь может располагаться отдельный раздел. Помогите Википедии, написав его. (31 октября 2016) |
Квантовая механика
| Этот раздел статьи ещё не написан. Здесь может располагаться отдельный раздел. Помогите Википедии, написав его. (31 октября 2016) |
Примечания
- ↑ Линейная алгебра / П. С. Александров // Большая советская энциклопедия : [в 30 т.] / гл. ред. А. М. Прохоров. — 3-е изд. — М. : Советская энциклопедия, 1969—1978.
- ↑ Клейнер, 2007, About 4000 years ago the Babylonians knew how to solve a system of two linear equations in two unknowns (a 2 × 2 system). In their famous Nine Chapters of the Mathematical Art the Chinese solved 3 × 3 systems by working solely with their (numerical) coefficients. These were prototypes of matrix methods, not unlike the “elimination methods” introduced by Gauss and others, p. 79.
- ↑ 1 2 Бурбаки, 1963, с. 74.
- ↑ 1 2 Бурбаки, 1963, с. 75.
- ↑ Прасолов, 1996, с. 9.
- ↑ Клейнер, 2007, p. 80.
- ↑ Прасолов, 1996, с. 10.
- ↑ Клейнер, 2007, The first publication to contain some elementary information on determinants was Maclaurin’s Treatise of Algebra, in which they were used to solve 2 × 2 and 3 × 3 systems, p. 81.
- ↑ Даан-Дальмедико, 1986, с. 394.
- ↑ Клейнер, 2007, p. 79.
- ↑ Бурбаки, 1963, с. 75—76.
- ↑ Бурбаки, 1963, с. 76.
- ↑ Бурбаки, 1963, с. 76—77, 134—137.
- ↑ Бурбаки, 1963, с. 77-78.
- ↑ 1 2 Бурбаки, 1963, с. 80.
- ↑ Даан-Дальмедико, 1986, с. 402.
- ↑ От лат. matrix — «первопричина». Во многих источниках считается, что термин ввёл Сильвестр в 1848 году, однако в том году он не опубликовал ни одной работы, см. J. J. Sylvester. The Collected Mathematical Papers of James Joseph Sylvester / H. F. Baker. — Cambridge: Cambridge University Press, 1904., тогда как в работе 1850 года J. J. Sylvester. Additions to the articles in the September number of this journal, “On a new class of theorems”, and on Pascal’s theorem (англ.) // The London, Edinburgh and Dublin Philosophical Magazine and Journal of Science. — Vol. XXXVII. — P. 363—370.: «…This will not in itself represent a determinant, but is, as it were, a Matrix out of which we may form various systems of determinants…»
- ↑ Клейнер, 2007, … the term “matrix” was coined by Sylvester in 1850, p. 82.
- ↑ 1 2 3 Бурбаки, 1963, с. 82.
- ↑ Клейнер, 2007, p. 81.
- ↑ 1 2 3 Бурбаки, 1963, с. 84.
- ↑ Шафаревич И. Р., Ремизов А. О. Линейная алгебра и геометрия. — Москва: Физматлит, 2009. — P. 511. — 1000 экз. — ISBN 978-5-9221-1139-3.
- ↑ Данфорд Н., Шварц Дж. Предисловие (Костюченко А. Г., научный редактор) // Линейные операторы. — М.: Иностранная литература, 1962. — С. 5—6. Однако в функциональном анализе есть несколько больших «традиционных» направлений, которые и поныне в значительной степени определяют его лицо. К их числу принадлежит и теория линейных операторов, которую иногда называют становым хребтом функционального анализа.
- ↑ Бурбаки, 1963, с. 85.
- ↑ Poole, D. Linear Algebra: A Modern Introduction. — 2nd edition. — Belmont: Brooks/Cole, 2006. — P. [179] (col. 1). — 714 p. — ISBN 0-534-99845-3.
- ↑ Ильин В. П. Линейная алгебра: от Гаусса до суперкомпьютеров будущего (англ.). Природа, 1999, №6 (1 июня 1999). Дата обращения: 2 мая 2013. Архивировано 10 мая 2013 года.
- ↑ Мальцев, 1970, с. 12.
- ↑ Мальцев, 1970, с. 55—59.
- ↑ Прасолов, 1996, с. 9—29.
- ↑ Векторное пространство — статья из Математической энциклопедии. Кадец М. И.
Литература
- Бурбаки. Линейная и полилинейная алгебра // Очерки по истории математики / И. Г. Башмакова (перевод с французского). — М.: Издательство иностранной литературы, 1963. — С. 73—86. — 292 с. — (Элементы математики).
- Гельфанд И. М. Лекции по линейной алгебре. — 5-е. — М.: Добросвет, МЦНМО, 1998. — 319 с. — ISBN 5-7913-0015-8.
- Даан-Дальмедико А., Пейффер Ж. Линейные структуры // Пути и лабиринты. Очерки по истории математики = Routes et dédales / Перевод с французского А. А. Брядинской под редакцией И. Г. Башмаковой. — М.: Мир, 1986. — С. 394—402. — 432 с. — (Современная математика. Популярная серия). — 50 000 экз.
- Israel Kleiner. History of Linear Algebra // A History of Abstract Algebra. — Boston: Birkhäuser, 2007. — P. 79—89. — 168 p. — ISBN 978-0-8176-4684-4. — doi:10.1007/978-0-8176-4685-1_5.
- Кострикин А. И., Манин Ю. И. Линейная алгебра и геометрия. — М.: Наука, 1986. — 304 с.
- Мальцев А. И. Основы линейной алгебры. — 3-е. — М.: Наука, 1970. — 400 с.
- Постников М. М. Линейная алгебра (Лекции по геометрии. Семестр II). — 2-е. — М.: Наука, 1986. — 400 с.
- Прасолов В. В. Задачи и теоремы линейной алгебры. — М.: Наука, 1996. — 304 с. — (Физматлит). — ISBN 5-02-014727-3.
- Стренг Г. Линейная алгебра и её применения = Linear Algebra and Its Applications. — М.: Мир, 1980. — 454 с.
- Фаддеев Д. К. Лекции по алгебре. — 5-е. — СПб.: Лань, 2007. — 416 с.
- Халмош П. Конечномерные векторные пространства = Finite-Dimensional Vector Spaces. — М.: Физматгиз, 1963. — 263 с.
- Шафаревич И. Р., Ремизов А. О. Линейная алгебра и геометрия. — М.: Физматлит, 2009. — 511 с.

 уравнений с n{displaystyle n}
уравнений с n{displaystyle n}
 не меняется от того, что над x{displaystyle x}
не меняется от того, что над x{displaystyle x} и y{displaystyle y}
и y{displaystyle y} совершается линейная подстановка (с целыми коэффициентами и определителем, равным 1), Лагранж в
совершается линейная подстановка (с целыми коэффициентами и определителем, равным 1), Лагранж в 
 , в ячейках которой расположены элементы произвольного заранее выбранного (основного)
, в ячейках которой расположены элементы произвольного заранее выбранного (основного) 
 , но обычно с матрицами оперируют как с едиными объектами: над матрицами определены
, но обычно с матрицами оперируют как с едиными объектами: над матрицами определены  и m×1{displaystyle mtimes 1}
и m×1{displaystyle mtimes 1} называются вектор-строка и вектор-столбец соответственно.
называются вектор-строка и вектор-столбец соответственно. ),
),  ),
),  ),
),  ), где P−1{displaystyle P^{-1}}
), где P−1{displaystyle P^{-1}} — матрица,
— матрица,  ), такие характеристики матриц, как
), такие характеристики матриц, как  векторов этого пространства являются линейно зависимыми. Такое векторное пространство называется n{displaystyle n}
векторов этого пространства являются линейно зависимыми. Такое векторное пространство называется n{displaystyle n} — векторов-столбцов и векторов-строк соответственно, а все операции векторной алгебры могут быть сведены к алгебре матрицː например, сложение векторов совпадает со сложением матриц, а векторное умножение векторов может быть
— векторов-столбцов и векторов-строк соответственно, а все операции векторной алгебры могут быть сведены к алгебре матрицː например, сложение векторов совпадает со сложением матриц, а векторное умножение векторов может быть  (количество измерений массива называют
(количество измерений массива называют  рассматривается как l{displaystyle l}
рассматривается как l{displaystyle l} раз
раз  раз
раз  , «тензор ранга (l,k){displaystyle (l,k)}
, «тензор ранга (l,k){displaystyle (l,k)} »).
»). ), обобщение которой на линейные пространства позволило обобщить и определение тензора: рассматривать тензор ранга (l,k){displaystyle (l,k)}
), обобщение которой на линейные пространства позволило обобщить и определение тензора: рассматривать тензор ранга (l,k){displaystyle (l,k)} как элемент тензорного произведения k{displaystyle k}
как элемент тензорного произведения k{displaystyle k} :
: .
. и кососимметричных (B(x,y)=−B(y,x)){displaystyle (B(x,y)=-B(y,x))}
и кососимметричных (B(x,y)=−B(y,x)){displaystyle (B(x,y)=-B(y,x))} билинейных форм.
билинейных форм. определяется как
определяется как  , элементы которого называются скалярами, притом векторы с операцией сложения векторов ⟨V,+⟩{displaystyle langle V,+rangle }
, элементы которого называются скалярами, притом векторы с операцией сложения векторов ⟨V,+⟩{displaystyle langle V,+rangle } образуют
образуют  такая, что выполнены следующие свойства (1,α,β∈F,v,u∈V{displaystyle 1,alpha ,beta in {mathfrak {F}},,mathbf {v} ,mathbf {u} in V}
такая, что выполнены следующие свойства (1,α,β∈F,v,u∈V{displaystyle 1,alpha ,beta in {mathfrak {F}},,mathbf {v} ,mathbf {u} in V} ):
): ,
, ,
, ,
, .
. , для совокупности векторов вводится линейной независимости (если существует нетривиальная линейная комбинация, обращающаяся в нуль абелевой группы пространства), вводится понятие
, для совокупности векторов вводится линейной независимости (если существует нетривиальная линейная комбинация, обращающаяся в нуль абелевой группы пространства), вводится понятие  — отображение, сохраняющее линейность:
— отображение, сохраняющее линейность: ,
, .
. имеет наиболее простой вид. При решении этой задачи ключевую роль играют
имеет наиболее простой вид. При решении этой задачи ключевую роль играют  — подпространства,
— подпространства,  (то есть, выполнено L(Wi)⊂Wi{displaystyle L(W_{i})subset W_{i}}
(то есть, выполнено L(Wi)⊂Wi{displaystyle L(W_{i})subset W_{i}} ),
),  , ni=dimWi{displaystyle n_{i}=dim W_{i}}
, ni=dimWi{displaystyle n_{i}=dim W_{i}} , на главной диагонали, если выбрать базис состоящим из k{displaystyle k}
, на главной диагонали, если выбрать базис состоящим из k{displaystyle k} -ая группа является базисом в подпространстве Wi{displaystyle W_{i}}
-ая группа является базисом в подпространстве Wi{displaystyle W_{i}} .
. , которое можно задать с помощью одного (любого) ненулевого вектора x∈W{displaystyle xin W}
, которое можно задать с помощью одного (любого) ненулевого вектора x∈W{displaystyle xin W} . В этом случае условие вложенности образа подпространства в себя принимает вид L(x)=λx{displaystyle L(x){=}lambda x}
. В этом случае условие вложенности образа подпространства в себя принимает вид L(x)=λx{displaystyle L(x){=}lambda x} с некоторым числом λ{displaystyle lambda }
с некоторым числом λ{displaystyle lambda } ; такая конструкция приводит к определению собственного вектора и собственного числа: если для некоторого вектора x≠0{displaystyle xneq 0}
; такая конструкция приводит к определению собственного вектора и собственного числа: если для некоторого вектора x≠0{displaystyle xneq 0} и числа λ{displaystyle lambda }
и числа λ{displaystyle lambda }

 .
.