История тригонометрии как науки о соотношениях между углами и сторонами треугольника и других геометрических фигур охватывает более двух тысячелетий. Большинство таких соотношений нельзя выразить с помощью обычных алгебраических операций, и поэтому понадобилось ввести особые тригонометрические функции, первоначально оформлявшиеся в виде числовых таблиц.
 Геодезические измерения (XVII век)
Геодезические измерения (XVII век)
Историки полагают, что тригонометрию создали древние астрономы; немного позднее её стали использовать в геодезии и архитектуре. Со временем область применения тригонометрии постоянно расширялась, и в наши дни она включает практически все естественные науки, технику и ряд других областей деятельности[1]. Особенно полезными тригонометрические функции оказались при изучении колебательных процессов; на них основан также гармонический анализ функций и другие инструменты анализа. Томас Пейн в своей книге «Век Разума» (1794) назвал тригонометрию «душой науки»[2].
Содержание
- 1 Ранний период
- 2 Древняя Греция
- 3 Средневековье
- 4 Новое время
- 5 Историки тригонометрии
- 6 См. также
- 7 Примечания
- 8 Литература
- 9 Ссылки
Ранний период
 Древнекитайская иллюстрация к теореме Пифагора
Древнекитайская иллюстрация к теореме Пифагора
Зачатки тригонометрии можно найти в математических рукописях древнего Египта, Вавилона и древнего Китая. 56-я задача из папируса Ринда (II тысячелетие до н. э.) предлагает найти наклон пирамиды, высота которой равна 250 локтей, а длина стороны основания — 360 локтей[3].
От вавилонской математики ведёт начало привычное нам измерение углов градусами, минутами и секундами (введение этих единиц в древнегреческую математику обычно приписывают Гипсиклу, II век до н. э.). Среди известных вавилонянам теорем была, например, такая: вписанный угол, опирающийся на диаметр круга — прямой[4]. Главным достижением этого периода стало соотношение, позже получившее имя теоремы Пифагора; Ван дер Варден считает, что вавилоняне открыли его между 2000 и 1786 годами до н. э.[5] Вполне возможно, что китайцы открыли его независимо (см. «Математика в девяти книгах»); неясно, знали ли общую формулировку теоремы древние египтяне, но прямоугольный «египетский треугольник» со сторонами 3, 4 и 5 был там хорошо известен и широко использовался[6].
Древняя Греция
Общее и логически связное изложение тригонометрических соотношений появилось в древнегреческой геометрии[7]. Греческие математики ещё не выделяли тригонометрию как отдельную науку — для них она была частью астрономии[8].
Плоская тригонометрия
Несколько теорем тригонометрического характера содержат «Начала» Евклида (IV век до н. э.). В первой книге «Начал» теоремы 18 и 19 устанавливают, что большей стороне треугольника соответствует больший противолежащий угол — и обратно, большему углу соответствует бо́льшая сторона. Теоремы 20 и 22 формулируют «неравенство треугольника»: из трёх отрезков можно составить треугольник тогда и только тогда, когда длина каждого меньше суммы длин двух других. Теорема 32 доказывает, что сумма углов треугольника равна 180°.
Во второй книге «Начал» теорема 12 представляет собой словесный аналог теоремы косинусов[9]:
В тупоугольных треугольниках квадрат на стороне, стягивающей тупой угол, больше [суммы] квадратов на сторонах, содержащих тупой угол, на дважды взятый прямоугольник, заключённый между одной из сторон при тупом угле, на которую падает перпендикуляр, и отсекаемым этим перпендикуляром снаружи отрезком при тупом угле.
Следующая за ней теорема 13 — вариант теоремы косинусов для остроугольных треугольников. Аналога теоремы синусов у греков не было, это важнейшее открытие было сделано гораздо позднее[10].
 Прямоугольный треугольник Аристарха: взаимное расположение Солнца, Луны и Земли во время квадратуры
Прямоугольный треугольник Аристарха: взаимное расположение Солнца, Луны и Земли во время квадратуры
Дальнейшее развитие тригонометрии связано с именем астронома Аристарха Самосского (III век до н. э.). В его трактате «О величинах и расстояниях Солнца и Луны» ставилась задача об определении расстояний до небесных тел; эта задача требовала вычисления отношения сторон прямоугольного треугольника при известном значении одного из углов. Аристарх рассматривал прямоугольный треугольник, образованный Солнцем, Луной и Землёй во время квадратуры. Ему требовалось вычислить величину гипотенузы (расстояние от Земли до Солнца) через катет (расстояние от Земли до Луны) при известном значении прилежащего угла (87°), что эквивалентно вычислению значения sin3∘{displaystyle ~sin 3^{circ }}
. По оценке Аристарха, эта величина лежит в промежутке от 1/20 до 1/18, то есть расстояние до Солнца в 20 раз больше, чем до Луны[11]; на самом деле Солнце почти в 400 раз дальше, чем Луна, ошибка возникла из-за неточности в измерении угла. Попутно Аристарх доказал неравенство, которое в современных терминах передаётся формулой:
- sinαsinβ<αβ<tgαtgβ.{displaystyle {frac {sin alpha }{sin beta }}<{frac {alpha }{beta }}<{frac {operatorname {tg} alpha }{operatorname {tg} beta }}.}
Это же неравенство содержится в «Исчислении песчинок» Архимеда[12]. В трудах Архимеда (III век до н. э.) имеется важная теорема деления хорд, по существу эквивалентная формуле синуса половинного угла[13][14]:
- sinα2=1−cosα2.{displaystyle sin {frac {alpha }{2}}={sqrt {frac {1-cos alpha }{2}}}.}
 Гиппарх Никейский, предполагаемый автор первых тригонометрических таблиц
Гиппарх Никейский, предполагаемый автор первых тригонометрических таблиц
В течение всего периода развития античной науки главным полем для приложения результатов плоской тригонометрии у греков оставалась астрономия. Помимо задачи о вычислении расстояний, привлечения тригонометрии требовало определение параметров системы эпициклов и/или эксцентров, представляющих движение светила в пространстве. Согласно широко распространённому мнению, эта проблема впервые была сформулирована и решена Гиппархом (середина II века до н. э.) при определении элементов орбит Солнца и Луны; возможно, аналогичными задачами занимались и астрономы более раннего времени. Ему же часто приписывают авторство первых тригонометрических таблиц, не дошедших до нас[15]. Впрочем, согласно некоторым реконструкциям, первые тригонометрические таблицы были составлены ещё в III веке до н. э., возможно, Аполлонием Пергским[16].
 Синус угла θ/2 равен полухорде единичной окружности
Синус угла θ/2 равен полухорде единичной окружности
Вместо современной функции синуса Гиппарх и другие древнегреческие математики обычно рассматривали зависимость длины хорды окружности от заданного центрального угла (или, что эквивалентно, от заданной дуги окружности, выраженной в угловой мере). В современной терминологии, длина хорды, стягивающей дугу θ единичной окружности, равна удвоенному синусу центрального угла θ/2. Это соответствие справедливо для любых углов: 0° < θ < 360°. На языке хорд были сформулированы первые открытые греками тригонометрические соотношения[1]. Например, современной формуле:
- sin2α+cos2α=1{displaystyle sin ^{2}alpha +cos ^{2}alpha =1}
соответствовала у греков теорема[17]:
- (chordα)2+(chord180∘−α)2=d2,{displaystyle (chord_{alpha })^{2}+(chord_{180^{circ }-alpha })^{2}=d^{2},}
где chordα{displaystyle chord_{alpha }}
— хорда для центрального угла α{displaystyle alpha } , d{displaystyle d} — диаметр круга.
При этом радиус круга не считался равным единице, как сейчас. Например, у Гиппарха радиус круга предположительно считался равным R=3438 единиц — при таком определении длина дуги окружности была равна угловой мере этой дуги, выраженной в минутах: 360⋅602π≈3438{displaystyle ~{frac {360cdot 60}{2pi }}approx 3438}
, и это облегчало вычисления. У Птолемея R=60 единиц. Согласно современным реконструкциям[15][18], величины хорд у Гиппарха были протабулированы с интервалом 7°30′. Возможно, в основе вычисления таблицы Гиппарха лежал метод, разработанный Архимедом и восходящий ещё к Аристарху[19].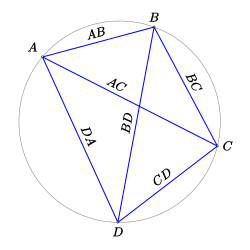 AB⋅CD+BC⋅AD={displaystyle ABcdot CD+BCcdot AD=}
AB⋅CD+BC⋅AD={displaystyle ABcdot CD+BCcdot AD=}
AC⋅BD{displaystyle ACcdot BD} (теорема Птолемея)
Позднее астроном II века Клавдий Птолемей в «Альмагесте» дополнил результаты Гиппарха. Тринадцать книг «Альмагеста» — самая значимая тригонометрическая работа всей античности. В частности, «Альмагест» содержит обширные пятизначные таблицы хорд для острых и тупых углов, с шагом 30 угловых минут[1]. Для вычисления хорд Птолемей использовал (в главе X) теорему Птолемея (известную, впрочем, ещё Архимеду), которая утверждает: сумма произведений длин противоположных сторон выпуклого вписанного в круг четырёхугольника равна произведению длин его диагоналей. Из этой теоремы нетрудно вывести две формулы для синуса и косинуса суммы углов и ещё две для синуса и косинуса разности углов, однако общая формулировка этих теорем у греков отсутствует[20].
Основным достижением античной тригонометрической теории стало решение в общем виде задачи «решения треугольников», то есть нахождения неизвестных элементов треугольника, исходя из трёх заданных его элементов (из которых хотя бы один является стороной)[7]. Впоследствии эта задача и её обобщения стали основной задачей тригонометрии[1]: заданы несколько (обычно три) известных элементов треугольника, требуется найти остальные связанные с ним величины. Первоначально в число элементов треугольника (известных или неизвестных) включали стороны и углы при вершинах, позже к ним добавились медианы, высоты, биссектрисы, радиус вписанной или описанной окружности, положение центра тяжести и т. д. Прикладные тригонометрические задачи отличаются большим разнообразием — например, могут быть заданы измеримые на практике результаты действий над перечисленными величинами (к примеру, сумма углов или отношение длин сторон).
Сферическая тригонометрия
Параллельно с развитием тригонометрии плоскости греки, под влиянием астрономии, далеко продвинули сферическую тригонометрию. В «Началах» Евклида на эту тему имеется только теорема об отношении объёмов шаров разного диаметра, но потребности астрономии и картографии вызвали быстрое развитие сферической тригонометрии и смежных с ней областей — системы небесных координат, теории картографических проекций, технологии астрономических приборов (в частности, была изобретена астролябия[21]).
Историки не пришли к консенсусу насчёт степени развития у античных греков геометрии небесной сферы. Некоторые исследователи приводят доводы, что эклиптическая или экваториальная система координат использовалась для записи результатов астрономических наблюдений по меньшей мере уже во времена Гиппарха[22]. Возможно, тогда были известны и некоторые теоремы сферической тригонометрии, которые могли использоваться для составления звёздных каталогов[23] и в геодезии.
Первые известные нам труды по «Сферике» (то есть сферической геометрии, с ясным астрономическим уклоном) написали[24]:
- (IV век до н. э.) Автолик из Питаны и Евклид («Феномены»).
- (II век до н. э.) Феодосий и Гипсикл.
Некоторые разобранные в этих сочинениях задачи носят тригонометрический характер, однако из-за слабой разработанности теории авторы ещё применяют обходные пути. Например, задачу «найти время полного восхода (захода) зодиакального созвездия» Гипсикл решает приближённо с помощью многоугольных чисел[24].
Решающим этапом в развитии теории стала монография «Сферика» в трёх книгах, которую написал Менелай Александрийский (около 100 года н. э.). В первой книге он изложил теоремы о сферических треугольниках, аналогичные теоремам Евклида о плоских треугольниках (см. I книгу «Начал»). Историки считают, что подход Менелая во многом опирается на труды Феодосия, которые у Менелая существенно расширены и приведены в систему. По сообщению Паппа, Менелай первым ввёл понятие сферического треугольника как фигуры, образованной отрезками больших кругов[25]. Менелай доказал теорему, для которой у Евклида нет плоского аналога: два сферических треугольника конгруэнтны (совместимы), если соответствующие углы равны. Другая его теорема утверждает, что сумма углов сферического треугольника всегда больше 180°[25].
Вторая книга «Сферики» излагает применение сферической геометрии к астрономии. Третья книга содержит важную для практической астрономии теорему Менелая, известную как «правило шести величин»[26]. Две другие открытые Менелаем фундаментальные теоремы впоследствии получили названия «правило четырёх величин» и «правило тангенсов»[25].
Несколько десятилетий спустя Клавдий Птолемей в своих трудах «География», «Аналемма» и «Планисферий» даёт подробное изложение тригонометрических приложений к картографии, астрономии и механике. Среди прочего, описана стереографическая проекция, исследованы несколько практических задач, например: определить высоту и азимут небесного светила по его склонению и часовому углу. С точки зрения тригонометрии, это значит, что надо найти сторону сферического треугольника по другим двум сторонам и противолежащему углу[27].
Сферической геометрии Птолемей посвятил также XIII главу в первой книге «Альмагеста»; в отличие от Менелая, Птолемей не привёл доказательств многих утверждений, но зато уделил много внимания алгоритмам, пригодным для практических вычислений в астрономии. Опорной конструкцией, вместо плоских хорд, в «Альмагесте» служит «четырёхсторонник Менелая». Для «решения» прямоугольного сферического треугольника, то есть для вычисления его характеристик, Птолемей привёл в словесной записи 4 теоремы; в современных обозначениях они имеют вид (угол C{displaystyle C}
прямой)[28]:
- sina=sinc⋅sinA{displaystyle sin a=sin ccdot sin A} (частный случай сферической теоремы синусов)
- tga=sinb⋅tgA{displaystyle operatorname {tg} a=sin bcdot operatorname {tg} A}
- cosc=cosa⋅cosb{displaystyle cos c=cos acdot cos b} (частный случай сферической теоремы косинусов)
- tgb=tgc⋅cosA{displaystyle operatorname {tg} b=operatorname {tg} ccdot cos A}
Поясним, что в сферической геометрии принято измерять стороны треугольника не линейными единицами, а величиной опирающихся на них центральных углов. В современной сферической тригонометрии приводятся ещё два соотношения:
- cosA=cosa⋅sinB{displaystyle cos A=cos acdot sin B} (тоже вытекает из сферической теоремы косинусов)
- cosc=ctgA⋅ctgB{displaystyle cos c=operatorname {ctg} Acdot operatorname {ctg} B}
У Птолемея они отсутствуют, поскольку их нельзя вывести из теоремы Менелая[28].
Средневековье
Индия
В IV веке, после гибели античной науки, центр развития математики переместился в Индию. Сочинения индийских математиков (сиддханты) показывают, что их авторы были хорошо знакомы с трудами греческих астрономов и геометров[29]. Чистой геометрией индийцы интересовались мало, но их вклад в прикладную астрономию и расчётные аспекты тригонометрии очень значителен.
 Определение тригонометрических функций в средневековой математике
Определение тригонометрических функций в средневековой математике
В первую очередь индийцы изменили некоторые концепции тригонометрии, приблизив их к современным. Они провели замену античных хорд на синусы (название «синус» восходит к слову «тетива» на санскрите[30]) в прямоугольном треугольнике. Тем самым в Индии было положено начало тригонометрии как общему учению о соотношениях в треугольнике, хотя, в отличие от греческих хорд, индийский подход ограничивался только функциями острого угла[31].
Синус индийцы определяли несколько иначе, чем в современной математике (см. рис. справа): под синусом понималась длина отрезка AD, опирающегося на дугу AC окружности радиуса R=3438 единиц (как у Гиппарха). Таким образом, «индийский синус» угла в 3438 раз больше современного синуса и имел размерность длины[30]. Из этого правила были исключения; например, Брахмагупта по неясным причинам принял радиус равным 3270 единиц[32].
Индийцы первыми ввели в использование косинус. Использовался ещё так называемый обращённый синус, или синус-верзус, равный длине отрезка DC на рисунке справа[33].
Как и у греков, тригонометрия индийцев развивалась главным образом в связи с её астрономическими приложениями, в основном для использовании в теории движения планет и для изучения небесной сферы. Это свидетельствует о хорошем знании сферической тригонометрии «Альмагеста» и «Аналеммы», однако ни одной их собственной работы, развивающей теорию этого раздела тригонометрии, не обнаружено[34]. Тем не менее в разработке прикладных алгоритмов решения астрономических задач индийцы достигли больших успехов[29]. Например, в «Панча-сиддхантике» Варахамихиры (VII в.) даётся оригинальное решение астрономической задачи, описанной у Птолемея: найти высоту Солнца над горизонтом, если известны широта местности, склонение Солнца и его часовой угол. Автор для решения применяет аналог теоремы косинусов[35], он же впервые привёл формулу для синуса половинного угла[36].
 Статуя Ариабхаты. Индийский межуниверситетский центр астрономии и астрофизики (IUCAA)
Статуя Ариабхаты. Индийский межуниверситетский центр астрономии и астрофизики (IUCAA)
Для астрономических расчётов был составлен ряд тригонометрических таблиц. Первые (четырёхзначные) таблицы синусов приведены в древней «Сурья-сиддханте» и у Ариабхаты («Ариабхатия», V век). Таблицы Ариабхаты содержат 24 значения синусов и синус-верзусов с интервалом 3°45′ (половина шага таблиц у Гиппарха).
Важный вклад в развитие тригонометрии внес Брахмагупта (VII в.), открывший несколько тригонометрических соотношений, в том числе и те, которые в современной записи приняли вид[35]:
- sin2α+cos2α=1{displaystyle sin ^{2}alpha +cos ^{2}alpha =1}
- sinα=cos(90∘−α){displaystyle sin alpha =cos(90^{circ }-alpha )}
Кроме того, индийцы знали формулы для кратных углов sinnφ{displaystyle sin nvarphi }
, cosnφ{displaystyle cos nvarphi } для n=2,3,4,5{displaystyle n=2,3,4,5} . В «Сурья-сиддханте» и в трудах Брахмагупты при решении задач фактически используется сферический вариант теоремы синусов, однако общая формулировка этой теоремы в Индии так и не появилась[37]. Историки нашли в индийских трудах неявное использование тангенсов, но важность этого понятия была осознана только позже, математиками исламских стран[29].
В трудах другого выдающегося ученого, Бхаскары II (XII век), приводятся формулы для синуса и косинуса суммы и разности углов:
- sin(α±β)=sinαcosβ±cosαsinβ,{displaystyle sin(alpha pm beta )=sin alpha cos beta pm cos alpha sin beta ,}
а также формула для малого приращения синуса:
- sinα−sinβ≈(α−β)cosβ{displaystyle sin alpha -sin beta approx (alpha -beta )cos beta }
(при α≈β{displaystyle alpha approx beta }
), соответствующая современному выражению для дифференциала синуса. Опираясь на формулу синуса суммы, Бхаскара опубликовал более точные и подробные, чем у Ариабхаты, тригонометрические таблицы с шагом 1°[38].
В XI веке мусульмане (Махмуд Газневи) захватили и разорили Северную Индию. Культурные центры переместились в Южную Индию, где образуется так называемая «школа Керала» (англ.) (рус. (по названию современного штата Керала на юге Индии)[39]. В XV—XVI веках математики Кералы в ходе астрономических исследований добились больших успехов в области суммирования бесконечных числовых рядов, в том числе для тригонометрических функций[37]. В анонимном трактате «Каранападдхати» («Техника вычислений») даны правила разложения синуса и косинуса в бесконечные степенные ряды[40], восходящие, вероятно, к основателю этой школы астроному Мадхаве из Сангамаграмы (1-я половина XV века)[41]. Мадхава и его последователь Нилаканта (в трактате «Taнтpacaнrpaха») приводят также правила разложения арктангенса в бесконечный степенной ряд. В Европе к подобным результатам подошли лишь в XVII—XVIII веках. Так, ряды для синуса и косинуса вывел Исаак Ньютон около 1666 года, а ряд арктангенса был найден Дж. Грегори в 1671 году и Г. В. Лейбницем в 1673 году[42].
Исламские страны
В VIII веке учёные стран Ближнего и Среднего Востока познакомились с трудами древнегреческих и индийских математиков и астрономов. Переводом их на арабский язык занимались такие крупные учёные VIII века, как Ибрахим Ал-Фазари и Якуб ибн Тарик. Далее они и их последователи стали активно комментировать и развивать эти теории. Опорной конструкцией у исламских учёных, как и у индийцев, был синус в треугольнике, или, что то же самое, полухорда в круге[34].
Их астрономические трактаты, аналогичные индийским сиддхантам, назывались «зиджи»; типичный зидж представлял собой сборник астрономических и тригонометрических таблиц, снабжённый руководством по их использованию и (не всегда) изложением общей теории[43]. Сравнение зиджей периода VIII—XIII веков показывает быструю эволюцию тригонометрических знаний. Предметом особого внимания ученых стран ислама была сферическая тригонометрия, методы которой использовались для решения задач астрономии и геодезии[44]. Среди основных решаемых проблем были следующие[45][43].
- — Точное определение времени суток.
- — Вычисление будущего расположения небесных светил, моментов их восхода и заката, затмений Солнца и Луны.
- — Нахождение географических координат текущего места.
- — Вычисление расстояния между городами с известными географическими координатами.
- — Определение направления на Мекку (кибла) из заданного места.
 Определение тангенса, котангенса, секанса и косеканса в средневековой арабской математике. Отрезок AD — гномон (вертикальный вверху или горизонтальный внизу), отрезок OD — его тень
Определение тангенса, котангенса, секанса и косеканса в средневековой арабской математике. Отрезок AD — гномон (вертикальный вверху или горизонтальный внизу), отрезок OD — его тень
Самые ранние из сохранившихся трудов принадлежат ал-Хорезми и ал-Марвази (IX век), которые рассмотрели, наряду с известными ещё индийцам синусом и косинусом, новые тригонометрические функции: тангенс, котангенс, секанс и косеканс[33]. Изначально эти функции определялись иначе, чем в современной математике. Так, под котангенсом понималась длина тени от вертикального гномона высотой 12 (иногда 7) единиц; первоначально эти понятия использовались для расчёта солнечных часов. Тангенсом называлась тень от горизонтального гномона. Косекансом и секансом назывались гипотенузы соответствующих прямоугольных треугольников (отрезки AO на рисунке справа)[46]. Лишь в X веке философ и математик ал-Фараби в своих комментариях к «Альмагесту» ввёл независимые от гномоники определения этих четырёх функций, определив их через синус и косинус в тригонометрическом круге птолемеевского радиуса (60 единиц). Основные соотношения между всеми шестью функциями привёл ал-Баттани в том же столетии. Окончательной унификации добился Абу-л-Вафа во второй половине X века, который впервые использовал для определения тригонометрических функций круг единичного радиуса, как это делается в современной математике.
Сабит ибн Курра (IX век) и ал-Баттани (X век) первыми открыли фундаментальную теорему синусов для частного случая прямоугольного сферического треугольника. Для произвольного сферического треугольника доказательство было найдено (разными способами и, вероятно, независимо друг от друга) Абу-л-Вафой, ал-Худжанди и ибн Ираком в конце X века[10]. В другом трактате ибн Ирака сформулирована и доказана теорема синусов для плоского треугольника[47].
Сферическая теорема косинусов в общем виде сформулирована в странах ислама не была, однако в трудах Сабита ибн Курры, ал-Баттани и других астрономов имеются эквивалентные ей утверждения. Вероятно, поэтому Региомонтан, впервые давший общую формулировку этой важного соотношения (XV век), назвал его «теоремой Альбатегния» (так тогда в Европе называли ал-Баттани)[48].
Ибн Юнис (X век) открыл преобразование произведения тригонометрических функций в сумму[49], например:
- sinαsinβ=cos(α−β)−cos(α+β)2,{displaystyle sin alpha sin beta ={frac {cos(alpha -beta )-cos(alpha +beta )}{2}},}
Формулы преобразования позволяли заменить трудоёмкое умножение на более простое сложение или вычитание. Впоследствии в Европе эти же формулы использовали для противоположной цели — замены сложения и вычитания на умножение, чтобы затем для вычисления результата применить логарифмические таблицы[50].
Одной из важнейших задач науки того времени являлось составление тригонометрических таблиц с как можно меньшим шагом. В IX веке ал-Хорезми составил таблицы синусов с шагом 1°, его современник Хаббаш аль-Хасиб (ал-Марвази) добавил к ним первые таблицы тангенсов, котангенсов и косекансов (с тем же шагом)[33]. В начале X века ал-Баттани опубликовал таблицы с шагом 30′, в конце того же столетия Ибн Юнис составил таблицы с шагом 1′[51]. При составлении таблиц ключевым было вычисление значения sin1∘{displaystyle sin 1^{circ }}
. Искусные методы для вычисления этой величины изобрели Ибн Юнис, Абу-л-Вафа, ал-Бируни. Наибольшего успеха добился в XV веке ал-Каши; в одной из своих работ он подсчитал, что sin1∘≈0,017452406437283571{displaystyle ~sin 1^{circ }approx 0{,}017452406437283571} (все знаки верны). В составленных при его участии «Астрономических таблицах» Самаркандской обсерватории Улугбека таблицы синусов вычислены с шестью шестидесятеричными знаками[52], с шагом 1′. Султан Улугбек лично участвовал в этой работе: он написал специальный трактат о вычислении синуса угла в 1°.Файл:Nesreddi tusi.jpg Насир ад-Дин ат-Туси
Первым специализированным трактатом по тригонометрии было сочинение среднеазиатского учёного ал-Бируни (X—XI век) «Книга ключей науки астрономии» (995—996 годы). Целый курс тригонометрии содержал главный труд ал-Бируни — «Канон Мас‘уда» (книга III). В дополнение к таблицам синусов (с шагом 15′) Ал-Бируни дал таблицы тангенсов (с шагом 1°). Идеологически труды Бируни близки к птолемеевским — на языке хорд он формулирует теоремы о синусе удвоенного и половинного угла, синусе суммы и разности углов[53]. Среди приложений книга Ал-Бируни показывает построение правильного вписанного девятиугольника и приближённое вычисление длины его стороны; этот алгоритм он использует для нахождения sin1∘{displaystyle ~sin 1^{circ }}
. В другом труде, «Геодезия», Бируни сообщил результаты собственных измерений длины земного меридиана, из которых следует оценка радиуса Земли, близкая к истинной (в пересчёте к метрической системе, Бируни получил 6340 км)[54].
Фундаментальное изложение тригонометрии как самостоятельной науки (как плоской, так и сферической) дал персидский математик и астроном Насир ад-Дин ат-Туси в 1260 году[55]. Его «Трактат о полном четырёхстороннике» содержит практические способы решения типичных задач, в том числе труднейших, решенных самим ат-Туси — например, построение сторон сферического треугольника по заданным трём углам[56]. Приведена теорема тангенсов для сферических треугольников, описано важное понятие полярного треугольника (впервые использованное в XI веке Ибн Ираком и ал-Джайяни). Сочинение ат-Туси стало широко известно в Европе и существенно повлияло на развитие тригонометрии.
Таким образом, к концу XIII века были открыты базовые теоремы, составляющие содержание тригонометрии:
- — Выражение любой тригонометрической функции через любую другую.
- — Формулы для синусов и косинусов кратных и половинных углов, а также для суммы и разности углов.
- — Теоремы синусов и косинусов.
- — Решение плоских и сферических треугольников
Из-за отсутствия алгебраической символики все перечисленные теоремы выражались в громоздкой словесной форме, но по существу были полностью эквивалентны современному их пониманию.
Европа
После того как арабские трактаты были в XII—XIII веках переведены на латынь, многие идеи индийских и персидских математиков стали достоянием европейской науки. По всей видимости, первое знакомство европейцев с тригонометрией состоялось благодаря зиджу ал-Хорезми, два перевода которого были выполнены в XII веке. Первоначально сведения о тригонометрии (правила её использования, таблицы некоторых тригонометрических функций) приводились в сочинениях по астрономии, однако в сочинении Фибоначчи «Практика геометрии», написанном около 1220 года, тригонометрия излагается как часть геометрии. Первым европейским сочинением, целиком посвященным тригонометрии, часто называют «Четыре трактата о прямых и обращенных хордах» английского астронома Ричарда Уоллингфордского (около 1320 г.). Книга содержит доказательство ряда тригонометрических тождеств и оригинальный метод вычисления синусов. Примерно в те же годы был написан трактат еврейского математика Леви бен Гершома (Герсонида) «О синусах, хордах и дугах», переведённый на латинский язык в 1342 году[57]. Книга содержит доказательство теоремы синусов и пятизначные таблицы синусов[58]. Тригонометрия затрагивается в «Теоретической геометрии» английского математика Томаса Брадвардина (написана в первой половине XIV в., опубликована в 1495 году). Тригонометрические таблицы, чаще переводные с арабского, но иногда и оригинальные, содержатся в сочинениях ряда других авторов XIV—XV веков. Тогда же тригонометрия заняла место среди университетских курсов.
Крупным достижением стала монография Региомонтана «Пять книг о треугольниках всех видов» (опубл. 1462—1464), в которой были сведены все известные к этому моменту знания по плоской и сферической тригонометрии и приложены семизначные таблицы синусов (с шагом 1′) и тангенсов (с шагом 1°). Немаловажно и то, что в таблицах Региомонтана, в нарушение астрономической традиции, впервые использовалась десятичная система (а не архаичная шестидесятеричная). Радиус тригонометрического круга Региомонтан принял равным 107{displaystyle 10^{7}}
, чтобы табличные значения были представлены целыми числами (десятичные дроби вошли в обиход несколько позднее, причём мощным стимулом к их применению стали именно тригонометрические вычисления[59]).
По сравнению с трактатом ат-Туси сочинение Региомонтана существенно полнее, оно содержит ряд новых задач, решённых оригинальными методами. Например, показывается, как построить треугольник, если известны одна его сторона, длина опущенной на неё высоты и противолежащий угол[60].
Новое время
 Фердинанд Боль, Портрет математика (1658). Диаграмма на стене показывает тригонометрические функции, определённые через окружность единичного радиуса
Фердинанд Боль, Портрет математика (1658). Диаграмма на стене показывает тригонометрические функции, определённые через окружность единичного радиуса
XVI—XVII века
Развитие тригонометрии в Новое время стало чрезвычайно важным не только для астрономии и астрологии, но и для других приложений, в первую очередь артиллерии, оптики и навигации при дальних морских путешествиях. Поэтому после XVI века этой темой занимались многие выдающиеся учёные, в том числе Николай Коперник, Иоганн Кеплер, Франсуа Виет[61]. Коперник посвятил тригонометрии две главы в своём трактате «О вращении небесных сфер» (1543). Вскоре (1551) появились 15-значные тригонометрические таблицы Ретика, ученика Коперника, с шагом 10″[62]. Кеплер опубликовал труд «Оптическая часть астрономии» (1604).
Потребность в сложных тригонометрических расчётах вызвала в начале XVII века открытие логарифмов, причём первые логарифмические таблицы Джона Непера содержали только логарифмы тригонометрических функций. Среди других открытий Непера — эффективный алгоритм решения сферических треугольников, получивший название «формулы аналогии Непера»[63].
Термин «тригонометрия» как название математической дисциплины ввёл в употребление немецкий математик Б. Питискус, опубликовавший в 1595 году книгу «Тригонометрия, или краткий и ясный трактат о решении треугольников» (лат. Trigonometria: sive de solutione triangulorum tractatus brevis et perspicuus). К концу XVII века появились современные названия тригонометрических функций. Термин «синус» впервые употребил около 1145 года английский математик и арабист Роберт Честерский?![30]. Региомонтан в своей книге назвал косинус «синусом дополнения» (лат. sinus complementi), поскольку cosx=sin(90∘−x){displaystyle ~cos x=sin(90^{circ }-x)}
; его последователи в XVII веке сократили это обозначение до co-sinus (Эдмунд Гунтер)[61], а позднее — до cos (Уильям Отред). Названия тангенса и секанса предложил в 1583 году датский математик Томас Финке[61], а упомянутый выше Эдмунд Гунтер ввёл названия котангенса и косеканса. Термин «тригонометрические функции» впервые употребил в своей «Аналитической тригонометрии» (1770) Георг Симон Клюгель[64]. Стандартные обозначения в треугольнике
Томас Финке предложил оригинальное решение геодезической задачи: найти углы треугольника, если известна их сумма α+β{displaystyle alpha +beta }
и отношение противолежащих сторон a:b{displaystyle a:b} . Для решения Финке использовал формулу Региомонтана (см. рисунок)[65]:
- a+ba−b=tgα+β2tgα−β2{displaystyle {frac {a+b}{a-b}}={frac {operatorname {tg} {frac {alpha +beta }{2}}}{operatorname {tg} {frac {alpha -beta }{2}}}}}
Виет в первой части своего «Математического канона» (1579) поместил разнообразные таблицы, в том числе тригонометрические, а во второй части дал обстоятельное и систематическое, хотя и без доказательств, изложение плоской и сферической тригонометрии. В 1593 году Виет подготовил расширенное издание этого капитального труда. «Несомненно, что самый интерес его к алгебре первоначально был вызван возможностью приложений к тригонометрии и астрономии»[66]. Другой важной заслугой Виета стало применение в тригонометрии разработанной им общей алгебраической символики; если ранее решение задачи понималось как геометрическое построение, то начиная с работ Виета приоритет начинает переходить к алгебраическим вычислениям[67]. Появление символики позволило записать в компактном и общем виде тригонометрические тождества — например, формулы для кратных углов[68]:
- cosmα=cosmα−m(m−1)1⋅2cosm−2α⋅sin2α+…{displaystyle cos malpha =cos ^{m}alpha -{frac {m(m-1)}{1cdot 2}}cos ^{m-2}alpha cdot sin ^{2}alpha +dots }
- sinmα=mcosm−1α⋅sinα−m(m−1)(m−2)1⋅2⋅3cosm−3α⋅sin3α+…{displaystyle sin malpha =mcos ^{m-1}alpha cdot sin alpha -{frac {m(m-1)(m-2)}{1cdot 2cdot 3}}cos ^{m-3}alpha cdot sin ^{3}alpha +dots }
Надо оговориться, что сам Виет ещё дал эти формулы частично в словесном описании, но при этом ясно указал на связь коэффициентов формул с биномиальными коэффициентами и привёл таблицу их значений для небольших значений m{displaystyle m}
[66].
Из других достижений Виета[69]: в работе «Дополнение к геометрии» Виет указал тригонометрический способ решения кубического уравнения для самого трудного в тот период — неприводимого — случая (стандартная формула требует умения работать с корнями из комплексных чисел). Виет дал первое в истории бесконечное произведение:
- 2π=cos90∘2⋅cos90∘4⋅cos90∘8…{displaystyle {frac {2}{pi }}=cos {frac {90^{circ }}{2}}cdot cos {frac {90^{circ }}{4}}cdot cos {frac {90^{circ }}{8}}dots }
Кроме артиллерии и навигации, тригонометрия быстро развивалась и в таких классических областях её применения, как геодезия. Широкое применение тангенсов объяснялось, в частности, простотой измерения с их помощью высоты горы или здания (см. рисунок):
- h=tgα tgβtgβ−tgαl{displaystyle h={frac {operatorname {tg} alpha operatorname {tg} beta }{operatorname {tg} beta -operatorname {tg} alpha }},l}
В 1615 году Снеллиус нашёл решение «задачи Снеллиуса-Потенота»: найти точку, из которой стороны данного (плоского) треугольника видны под заданными углами. Он открыл закон преломления света: для заданных исходной и преломляющей среды отношение синусов угла падения и угла преломления постоянно. Тем самым Снеллиус открыл дорогу новым применениям тригонометрических функций в оптике, а изобретение в эти же годы первых телескопов придало этому открытию особую важность.
 Синусоида в книге Альбрехта Дюрера (1525)
Синусоида в книге Альбрехта Дюрера (1525)
Первый график синусоиды появился в книге Альбрехта Дюрера «Руководство к измерению циркулем и линейкой» (нем. Underweysung der Messung mit dem Zirkel und Richtscheyt, 1525 год)[70]. В 1630-х годах Жиль Роберваль, в ходе своих исследований циклоиды, независимо вычертил синусоиду[71], он же опубликовал формулу тангенса двойного угла[50]. Джон Валлис в своей «Механике» (1670), опередив своё время, правильно указал знаки синуса во всех квадрантах и указал, что у синусоиды бесконечно много «оборотов». График тангенса для первого квадранта впервые начертил Джеймс Грегори (1668)[72].
Во второй половине XVII века началось стремительное развитие общей теории квадратур (то есть вычисления площади), завершившееся появлением в конце века математического анализа. Для тригонометрических функций важные результаты в начале этого периода получил Блез Паскаль (опубликованы в его книге «Письма А. Деттонвилля о некоторых его геометрических открытиях», 1659 год). В современной терминологии, Паскаль вычислил интегралы от натуральных степеней синуса и косинуса и некоторые связанные с ними[73], а также отметил, что d(sinx)=cosx dx{displaystyle ~d(sin x)=cos x dx}
. Работы в области тригонометрии проводили такие крупные математики XVII века, как Отред, Гюйгенс, Озанам, Валлис. Заметным процессом во второй половине XVII века стала постепенная алгебраизация тригонометрии, совершенствование и упрощение её символики (хотя до Эйлера символика была всё же гораздо более громоздка, чем современная)[74].
XVIII век
После открытия математического анализа сначала Джеймс Грегори, а затем Исаак Ньютон получили разложение тригонометрических функций (а также обратных к ним) в бесконечные ряды. Ньютон посвятил проблемам геометрии и тригонометрии 10 задач в своей книге «Универсальная арифметика»[75]. Например, в задаче X требуется «решить треугольник», если известны одна его сторона, противолежащий угол и сумма двух других сторон. Предложенный Ньютоном метод решения представляет собой одну из формул Мольвейде[76].
Лейбниц строго доказал, что sinx{displaystyle sin x}
не может быть, вообще говоря, алгебраически выражен через x{displaystyle x} , то есть, в современной терминологии, тригонометрические функции трансцендентны[77].
Важными открытиями в начале XVIII века стали:
- — Открытие и широкое распространение радианной меры углов[78] (Роджер Котс, 1714). Сам термин «радиан» появился позднее, его в 1873 году предложил английский инженер Джеймс Томсон[79].
- — Тригонометрическое представление комплексного числа и формула Муавра.
- (cosφ+isinφ)n=cosnφ+isinnφ {displaystyle (cos varphi +isin varphi )^{n}=cos nvarphi +isin nvarphi }
- — Начало использования (Ньютон и Грегори) полярной системы координат, связанной с декартовой тригонометрическими соотношениями; в общее употребление эти координаты ввёл Эйлер (1748)[80].
В 1706 году швейцарский математик Якоб Герман опубликовал формулы для тангенса суммы и тангенса кратных углов, а Иоганн Ламберт в 1765 году нашёл чрезвычайно полезные формулы, выражающие разные тригонометрические функции через тангенс половинного угла[81]. Исследуя гиперболические функции (1761), Ламберт показал, что их свойства аналогичны свойствам тригонометрических; причину этого ещё в 1707 году обнаружил Муавр: при замене вещественного аргумента на мнимый круг переходит в гиперболу, а тригонометрические функции — в соответствующие гиперболические[82].
Немецкий математик Фридрих Вильгельм фон Оппель (нем.) (рус. в книге «Анализ треугольников» (1746) опубликовал в современной записи обе формулы Мольвейде[83].
В книге «Полигонометрия» (1789) Симон Люилье обобщил тригонометрические соотношения для треугольников, дав их аналоги для произвольных многоугольников, включая пространственные. В работах на эту тему Люилье привёл основную теорему полигонометрии: площадь каждой грани многогранника равна сумме произведений площадей остальных граней на косинусы углов, образуемых ими с первой гранью. Он рассмотрел способы «решения многоугольников» с n{displaystyle n}
сторонами при различных постановках задачи: заданы n−1{displaystyle ~n-1} сторона и n−2{displaystyle ~n-2} угла, или все углы и n−2{displaystyle ~n-2} стороны, или все стороны и n−3{displaystyle ~n-3} угла[84].
В 1798 году Лежандр доказал, что если размеры сферического треугольника малы по сравнению с радиусом сферы, то при решении тригонометрических задач можно применять формулы плоской тригонометрии, вычтя при этом из каждого угла треть сферического избытка[85].
Манера обозначать обратные тригонометрические функции с помощью приставки arc (от лат. arcus — дуга) появилась у австрийского математика Карла Шерфера (Karl Scherffer, 1716—1783) и закрепилась благодаря Лагранжу. Имелось в виду, что, например, обычный синус позволяет по дуге окружности найти стягивающую её хорду, а обратная функция решает противоположную задачу. Английская и немецкая математические школы до конца XIX века предлагали иные обозначения: sin−1,1sin{displaystyle sin ^{-1},{frac {1}{sin }}}
, но они не прижились[86].
Реформы Леонарда Эйлера
Современный вид тригонометрии придал Леонард Эйлер. В трактате «Введение в анализ бесконечных» (1748) Эйлер дал определение тригонометрических функций, эквивалентное современному[75], и соответственно определил обратные функции. Если его предшественники понимали синус и прочие понятия геометрически, то есть как линии в круге или треугольнике, то после работ Эйлера sinx, cosx, tgx{displaystyle sin x,~cos x,~operatorname {tg} x}
и т. д. стали рассматриваться как безразмерные аналитические функции действительного и комплексного переменного. Для комплексного случая он установил связь тригонометрических функций с показательной функцией (формула Эйлера). Подход Эйлера с этих пор стал общепризнанным и вошёл в учебники.
Эйлер рассматривал как допустимые отрицательные углы и углы, большие 360°, что позволило определить тригонометрические функции на всей вещественной числовой прямой, а затем продолжить их на комплексную плоскость. Когда встал вопрос о распространении тригонометрических функций на тупые углы, знаки этих функций до Эйлера нередко выбирались ошибочно; многие математики считали, например, косинус и тангенс тупого угла положительными[71]. Эйлер определил эти знаки для углов в разных координатных квадрантах, исходя из формул приведения[87].
Эйлер впервые представил разложение тригонометрических функций в бесконечные произведения (1734), откуда вывел ряды для их логарифмов[88].
В других трудах, в первую очередь «Основания сферической тригонометрии, выведенные из метода максимумов и минимумов» (1753) и «Всеобщая сферическая тригонометрия, кратко и ясно выведенная из первых оснований» (1779), Эйлер впервые дал полное систематическое изложение сферической тригонометрии на аналитическом основании[89], причём многие крупные результаты принадлежат самому Эйлеру.
В середине XVIII века разгорелся важнейший по своим последствиям «спор о струне»[90]. Эйлер в полемике с Даламбером предложил более общее определение функции, чем принималось ранее; в частности, функция может быть задана тригонометрическим рядом. В своих трудах Эйлер использовал несколько представлений алгебраических функций в виде ряда из кратных аргументов тригонометрических функций, например[91]:
- π−x2=sinx+sin2×2+sin3×3…{displaystyle {frac {pi -x}{2}}=sin x+{frac {sin 2x}{2}}+{frac {sin 3x}{3}}dots }
Общей теорией тригонометрических рядов Эйлер не занимался и сходимость полученных рядов не исследовал, но получил несколько важных результатов. В частности, он вывел разложения целых степеней синуса и косинуса[91].
Тригонометрия в России
В России первые сведения о тригонометрии были опубликованы в сборнике «Таблицы логарифмов, синусов и тангенсов к изучению мудролюбивых тщателей», опубликованном при участии Л. Ф. Магницкого в 1703 году[92]. В 1714 году появилось содержательное руководство «Геометрия практика», первый русский учебник по тригонометрии, ориентированный на прикладные задачи артиллерии, навигации и геодезии[93]. Завершением периода освоения тригонометрических знаний в России можно считать фундаментальный учебник академика М. Е. Головина (ученика Эйлера) «Плоская и сферическая тригонометрия с алгебраическими доказательствами» (1789).
В конце XVIII века в Петербурге возникла авторитетная тригонометрическая школа (А. И. Лексель, Н. И. Фусс, Ф. И. Шуберт), которая внесла большой вклад в плоскую и сферическую тригонометрию[64].
XIX—XXI века
В начале XIX века Н. И. Лобачевский добавил к плоской и сферической тригонометрии третий раздел — гиперболическую (для геометрии Лобачевского, первую работу в этой области опубликовал Ф. А. Тауринус в 1826 году). Лобачевский показал, что формулы сферической тригонометрии переходят в формулы гиперболической тригонометрии при замене длин сторон треугольника a, b, c на мнимые величины: ai, bi, ci — или, что эквивалентно, при замене тригонометрических функций на соответствующие гиперболические[94].
В XIX—XX веках бурное развитие получили теория тригонометрических рядов и связанные с ней области математики: гармонический анализ, теория случайных процессов, кодирование аудио и видеоинформации и другие. Ещё Даниил Бернулли высказал убеждение, что любую (непрерывную) функцию на заданном промежутке можно представить тригонометрическим рядом[95]. Дискуссии продолжались до 1807 года, когда Фурье опубликовал теорию представления произвольных кусочно-аналитических функций тригонометрическими рядами (окончательный вариант содержится в его «Аналитической теории тепла», 1822)[90]. Для разложения функции f(x){displaystyle f(x)}
в ряд:
- f(x)=a0+∑n=1∞(ancosnx+bnsinnx).{displaystyle f(x)=a_{0}+displaystyle sum _{n=1}^{infty }(a_{n}cos {nx}+b_{n}sin {nx}).}
Фурье привёл интегральные формулы расчёта коэффициентов[90]:
- an=1π∫02πf(x)cosnxdx(n=0,1,2,…);bn=1π∫02πf(x)sinnxdx(n=1,2,3,…){displaystyle a_{n}={frac {1}{pi }}displaystyle int limits _{0}^{2pi }!f(x)cos {nx},dxquad (n=0,1,2,dots );quad b_{n}={frac {1}{pi }}displaystyle int limits _{0}^{2pi }!f(x)sin {nx},dxquad (n=1,2,3,dots )}
Изложение Фурье не было строгим в современном понимании, но уже содержало исследование сходимости большинства полученных им рядов. Для функций, заданных на всей числовой прямой и не являющихся периодическими, Фурье предложил разложение в интеграл Фурье.
Универсальность и эффективность методов анализа Фурье произвели большое впечатление на научный мир. Если ранее тригонометрические ряды использовались в математической физике преимущественно для изучения периодических процессов (колебания струны, небесная механика, движение маятника и т. п.), то в труде Фурье исследовались процессы совсем иного рода (теплопередача), и тригонометрические ряды помогли получить ценные практические результаты. С этого момента тригонометрические ряды и интегралы стали мощным инструментом анализа разнообразных функций. Результаты Фурье продолжили и углубили Пуассон и Коши, вопрос сходимости рядов детально исследовали Дирихле и другие математики[96]. Риман в своей диссертации исследовал произвольные тригонометрические ряды, не обязательно связанные с разложением какой-либо функции (1853), сформулировал для них «принцип локализации». Вопрос о представимости произвольной измеримой и конечной почти всюду функции тригонометрическим рядом (который не обязательно совпадает с её рядом Фурье) был решён в 1941 году теоремой Меньшова.
Исследуя множества особых точек для тригонометрических рядов, Георг Кантор разработал фундаментальную для всей математики теорию множеств[97]. Огромное влияние теория тригонометрических рядов оказала на развитие комплексного анализа, математической физики, электроники и многих других разделов науки[90]. Теория функций вещественного переменного, теория меры и интеграл Лебега появились и далее развивались в тесной связи с теорией тригонометрических рядов[90][98]. Важные практические применения имеет приближение функций конечными тригонометрическими полиномами[99] (используемое также для интерполирования).
Историки тригонометрии
В XVIII—XIX веках труды по истории математики и астрономии значительное внимание уделяли и истории тригонометрии (Ж. Э. Монтукла, Ж. Б. Ж. Деламбр, Г. Ганкель, П. Таннери и другие). В 1900 году немецкий историк математики Антон фон Браунмюль (нем.) (рус. опубликовал первую монографию в двух томах, специально посвящённую истории тригонометрии[100]. В XX веке крупные работы по этой теме опубликовали И. Г. Цейтен, М. Б. Кантор, О. Нейгебауэр, Б. А. Розенфельд, Г. П. Матвиевская и другие.
См. также
- Астрономия Древней Греции
- Астрономия исламского Средневековья
- История математики
- Тригонометрические тождества
Примечания
- ↑ 1 2 3 4 Выгодский М. Я. Справочник по элементарной математике. — М.: Наука, 1978. — С. 266-268..
- ↑ Paine, Thomas. The Age of Reason. — Dover Publications, 2004. — С. 52.
- ↑ Eli Maor. Trigonometric Delights. — Princeton University Press, 1998. — P. 20. — ISBN 0-691-09541-8.
- ↑ Глейзер Г. И., 1982, с. 95..
- ↑ van der Waerden, Bartel Leendert. Geometry and Algebra in Ancient Civilizations. — Springer, 1983. — ISBN 3-540-12159-5.
- ↑ Ван дер Варден, 1959, с. 13, подстрочное примечание.
- ↑ 1 2 Глейзер Г. И., 1982, с. 77..
- ↑ Цейтен Г. Г., 1938, с. 124-125..
- ↑ Глейзер Г. И., 1982, с. 94-95..
- ↑ 1 2 Матвиевская Г. П., 2012, с. 92-96..
- ↑ Цейтен Г. Г., 1932, с. 153-154..
- ↑ Веселовский, 1961, с. 38..
- ↑ Матвиевская Г. П., 2012, с. 15..
- ↑ Boyer, Carl B. A History of Mathematics. — Second ed.. — John Wiley & Sons, Inc., 1991. — P. 158–159.. — ISBN 0-471-54397-7.
- ↑ 1 2 Toomer, 1973.
- ↑ Van der Waerden, 1988.
- ↑ Сираждинов С. Х., Матвиевская Г. П., 1978, с. 77..
- ↑ Thurston, 1994.
- ↑ Duke, 2011.
- ↑ Хрестоматия по истории математики, 1976, с. 195-197..
- ↑ Матвиевская Г. П., 2012, с. 25-27..
- ↑ Duke, 2002.
- ↑ Sidoli, 2004.
- ↑ 1 2 Матвиевская Г. П., 2012, с. 27-33..
- ↑ 1 2 3 Матвиевская Г. П., 2012, с. 33-36..
- ↑ История математики, том I, 1970, с. 141-142..
- ↑ Цейтен Г. Г., 1932, с. 158-162..
- ↑ 1 2 Матвиевская Г. П., 2012, с. 36-39..
- ↑ 1 2 3 Матвиевская Г. П., 2012, с. 40-44..
- ↑ 1 2 3 История математики в Средние века, 1961, с. 156-158..
- ↑ Глейзер Г. И., 1982, с. 81-82..
- ↑ Scott J. F., 1958, с. 50..
- ↑ 1 2 3 Сираждинов С. Х., Матвиевская Г. П., 1978, с. 79..
- ↑ 1 2 Scott J. F., 1958, с. 52..
- ↑ 1 2 История математики, том I, 1970, с. 199-201..
- ↑ История математики в Средние века, 1961, с. 157..
- ↑ 1 2 История математики в Средние века, 1961, с. 160..
- ↑ История математики в Средние века, 1961, с. 159..
- ↑ Бахмутская Э. Я. Степенные ряды для sint и cost в работах индийских математиков XV—XVIII вв. // Историко-математические исследования. — М.: Физматгиз, 1960. — № 13. — С. 325-335..
- ↑ Roy, Ranjan. Discovery of the Series Formula for π by Leibniz, Gregory, and Nilakantha // Math. Assoc. Amer. Mathematics Magazine. — 1990. — Вып. 63 (5). — С. 291–306.
- ↑ Plofker, 2009.
- ↑ История математики, том I, 1970, с. 203..
- ↑ 1 2 Матвиевская Г. П., 2012, с. 51-55..
- ↑ Хрестоматия по истории математики, 1976, с. 204-205.
- ↑ История математики, том I, 1970, с. 236-238..
- ↑ История математики, том I, 1970, с. 234-235..
- ↑ Матвиевская Г. П., 2012, с. 111..
- ↑ Матвиевская Г. П., 2012, с. 96-98..
- ↑ Матвиевская Г. П., 2012, с. 69..
- ↑ 1 2 Глейзер Г. И., 1983, с. 60..
- ↑ Матвиевская Г. П., 2012, с. 71-78..
- ↑ Хрестоматия по истории математики, 1976, с. 195-198,.
- ↑ Сираждинов С. Х., Матвиевская Г. П., 1978, с. 82..
- ↑ Сираждинов С. Х., Матвиевская Г. П., 1978, с. 88..
- ↑ Туси Насирэддин. Трактат о полном четырёхстороннике. Баку, Изд. АН АзССР, 1952.
- ↑ Рыбников К. А., 1960, с. 105..
- ↑ Этот трактат был включён в состав «Астрономии», одной из шести частей фундаментального теолого-философско-научного трактата «Войны Господа», над которым Герсонид трудился в ходе всей его жизни.
- ↑ Rabinovich, Nachum L. Рабби Леви бен Гершом и происхождение метода математической индукции. = Rabbi Levi ben Gershom and the origins of mathematical induction // Archive for History of Exact Sciences. — 1970. — В. 6. — С. 237—248.
- ↑ Вилейтнер Г., 1960, с. 14, 30-31..
- ↑ Цейтен Г. Г., 1932, с. 223-224..
- ↑ 1 2 3 Глейзер Г. И., 1982, с. 79, 84..
- ↑ История математики, том I, 1970, с. 320..
- ↑ Степанов Н. Н. §42. Формулы «аналогии Непера» // Сферическая тригонометрия. — М.—Л.: ОГИЗ, 1948. — С. 87-90. — 154 с.
- ↑ 1 2 Вилейтнер Г., 1960, с. 341-343..
- ↑ Цейтен Г. Г., 1938, с. 126-127..
- ↑ 1 2 Цейтен Г. Г., 1938, с. 129..
- ↑ Александрова Н. В., 2008, с. 189..
- ↑ Рыбников К. А., 1960, с. 125..
- ↑ Цейтен Г. Г., 1938, с. 130-132..
- ↑ Хайрер Э., Ваннер Г. Математический анализ в свете его истории. — М.: Научный мир, 2008. — С. 42. — 396 с. — ISBN 978-5-89176-485-9.
- ↑ 1 2 Глейзер Г. И., 1982, с. 86..
- ↑ Вилейтнер Г., 1960, с. 324-325..
- ↑ Цейтен Г. Г., 1938, с. 283-288..
- ↑ Вилейтнер Г., 1960, с. 327-335..
- ↑ 1 2 История математики, том III, 1972, с. 205-209..
- ↑ Вилейтнер Г., 1960, с. 331..
- ↑ Цейтен Г. Г., 1938, с. 419..
- ↑ O’Connor, J. J.; Robertson, E. F. Biography of Roger Cotes (неопр.). The MacTutor History of Mathematics (February 2005). Архивировано 24 сентября 2012 года.
- ↑ Александрова Н. В., 2008, с. 152..
- ↑ Александрова Н. В., 2008, с. 80-81..
- ↑ Вилейтнер Г., 1960, с. 322, 329..
- ↑ Александрова Н. В., 2008, с. 207..
- ↑ Вилейтнер Г., 1960, с. 334..
- ↑ Вилейтнер Г., 1960, с. 345..
- ↑ Степанов Н. Н. Сферическая тригонометрия. — Изд. 2-е. — М.—Л.: ГИТТЛ, 1948. — С. 139-143. — 154 с.
- ↑ Александрова Н. В., 2008, с. 211..
- ↑ История математики, том III, 1972, с. 323..
- ↑ Вилейтнер Г., 1960, с. 148, 336..
- ↑ История математики, том III, 1972, с. 209-215..
- ↑ 1 2 3 4 5 Тригонометрический ряд // Математическая энциклопедия (в 5 томах). — М.: Советская Энциклопедия, 1982. — Т. 5.
- ↑ 1 2 Паплаускас А. Б., 1966, с. 7, 15..
- ↑ Глейзер Г. И. История математики в школе. — М.: Просвещение, 1964. — С. 287. — 376 с.
- ↑ См.: Юшкевич А. П. Главы по истории математики в средние века. — В кн.: История естествознания в России. М.: 1957, т. I, с 45—48.
- ↑ См. статью Б. А. Розенфельда в книге: Каган В. Ф. Основания геометрии. Том II, стр. 313—321.
- ↑ Паплаускас А. Б., 1966, с. 26-27..
- ↑ Паплаускас А. Б., 1966, Глава IV..
- ↑ Даубен, Джозеф У. Георг Кантор и рождение теории трансфинитных множеств // Scientific American, издание на русском языке. — 1983. — Вып. 8 (август). — С. 76–86.
- ↑ Тригонометрический ряд (неопр.). Дата обращения: 28 октября 2012. Архивировано 23 ноября 2012 года.
- ↑ Тригонометрический полином // Математическая энциклопедия (в 5 томах). — М.: Советская Энциклопедия, 1982. — Т. 5.
- ↑ Braunmühl A. Vorlesungen über die Geschichte der Trigonometrie. — Leipzig, 1900—1903.
Литература
- Книги
- Александрова Н. В. История математических терминов, понятий, обозначений: Словарь-справочник, изд. 3-е. — СПб.: ЛКИ, 2008. — 248 с. — ISBN 978-5-382-00839-4.
- Ван дер Варден Б. Л. Пробуждающаяся наука. Математика древнего Египта, Вавилона и Греции. — М.: ГИФМЛ, 1959.
- Вилейтнер Г. История математики от Декарта до середины XIX столетия. — М.: ГИФМЛ, 1960. — 468 с.
- Глейзер Г. И. История математики в школе. VII-VIII классы. Пособие для учителей. — М.: Просвещение, 1982. — С. 76-95. — 240 с.
- Глейзер Г. И. История математики в школе. IX-X классы. Пособие для учителей. — М.: Просвещение, 1983. — 352 с.
- История математики под редакцией А. П. Юшкевича в трёх томах, М.: Наука.
- История математики. С древнейших времен до начала Нового времени // История математики / Под редакцией А. П. Юшкевича, в трёх томах. — М.: Наука, 1970. — Т. I. — 351 с.
- Математика XVII столетия // История математики / Под редакцией А. П. Юшкевича, в трёх томах. — М.: Наука, 1970. — Т. II. — 300 с.
- Математика XVIII столетия // История математики / Под редакцией А. П. Юшкевича, в трёх томах. — М.: Наука, 1972. — Т. III. — 495 с.
- Матвиевская Г. П. Очерки истории тригонометрии: Древняя Греция. Средневековый Восток. Позднее Средневековье. — Изд. 2-е. — М.: Либроком, 2012. — 160 с. — (Физико-математическое наследие: математика (история математики)). — ISBN 978-5-397-02777-9.
- Паплаускас А. Б. Тригонометрические ряды. От Эйлера до Лебега. — М.: Наука, 1966. — 277 с.
- Рожанская М. М. Механика на средневековом Востоке. — Москва: Наука, 1976.
- Рыбников К. А. История математики в двух томах. — М.: Изд. МГУ, 1960. — Т. I.
- Сираждинов С. Х., Матвиевская Г. П. Абу Райхан Беруни и его математические труды. Пособие для учащихся. — М.: Просвещение, 1978. — 95 с. — (Люди науки).
- Стройк Д. Я. Краткий очерк истории математики, изд. 3-е. — М.: Наука, 1978. — 336 с.
- Стройк Д. Я. (Dirk J. Struik). Краткий очерк истории математики, изд. 5-е. — М.: Наука, Гл. ред. физ.-мат. литературы, 1990. — 256 с. — ISBN 5-02014329-4.
- Хрестоматия по истории математики. Арифметика и алгебра. Теория чисел. Геометрия / Под ред. А. П. Юшкевича. — М.: Просвещение, 1976. — 318 с.
- Цейтен Г. Г. История математики в древности и в средние века. — М.—Л.: ГТТИ, 1932. — 230 с.
- Цейтен Г. Г. История математики в XVI и XVII веках. — М.—Л.: ОНТИ, 1938. — 456 с.
- Юшкевич А. П. История математики в Средние века. — М.: ГИФМЛ, 1961. — 448 с.
- Plofker K. Mathematics in India. — Princeton: Princeton University Press, 2009.
- Scott J. F. A History of Mathematics From Antiquity to the Beginning of the Nineteen Century. — London: Tailor & Francis Ltd, 1958. — 266 p.
- Thurston H. Early astronomy. — New York: Springer-Verlag, 1994.
- Van Brummelen G. The Mathematics of the Heavens and the Earth: The Early History of Trigonometry. — Princeton University Press, 2009.
- Статьи
- Веселовский И. Н. Аристарх Самосский — Коперник античного мира // Историко-астрономические исследования, вып. VII. — М., 1961. — С. 17—70.
- Матвиевская Г. П. Сферика и сферическая тригонометрия в древности и на средневековом Востоке // Развитие методов астрономических исследований, Вып. 8. — М.—Л., 1979.
- Bond J. D. The Development of Trigonometric Methods down to the Close of the XVth Century // Isis. — 1921. — Vol. 4, № 2. — P. 295—323.
- Duke D. Hipparchus’ Coordinate System // Arch. Hist. Exact Sci. — 2002. — Vol. 56. — P. 427—433.
- Duke D. The Very Early History of Trigonometry // DIO: The International Journal of Scientific History. — 2011. — Vol. 17. — P. 34—42.
- Kennedy E. S. The history of trigonometry // Historical Topics for the Mathematics Classroom: Thirty-first Yearbook. — Washington, D.C.: National Council of Teachers of Mathematics, 1969.
- Moussa A. The trigonometric functions, as they were in the arabic-islamic civilization // Arabic Sciences and Philosophy. — 2010. — Vol. 20. — P. 93—104.
- Sidoli N. Hipparchus and the Ancient Metrical Methods on the Sphere // Journal of the History of Astronomy. — 2004. — Vol. 35. — P. 71—84.
- Toomer G. J. The Chord Table of Hipparchus and the Early History of Greek Trigonometry // Centaurus. — 1973. — Vol. 18. — P. 6—28.
- Van der Waerden B. L. Reconstruction of a Greek table of chords // Arch. Hist. Exact Sci. — 1988. — Vol. 38. — P. 23—38.
Ссылки
- Федосова М. Тригонометрия (неопр.). Энциклопедия Кругосвет. Дата обращения: 5 июня 2012. Архивировано 24 сентября 2012 года..
- O’Connor, J. J.; Robertson E. F. Trigonometric functions (англ.). MacTutor History of Mathematics Archive (1996). Дата обращения: 5 июня 2012. Архивировано 24 сентября 2012 года..
- Leo Rogers. The History of Trigonometry (англ.). Дата обращения: 19 октября 2012. Архивировано 28 октября 2012 года..
| Эта статья входит в число избранных статей русскоязычного раздела Википедии. |
| Эта статья победила на конкурсе статьи года и была признана статьёй 2012 года русской Википедии. |

 . По оценке Аристарха, эта величина лежит в промежутке от 1/20 до 1/18, то есть расстояние до Солнца в 20 раз больше, чем до Луны
. По оценке Аристарха, эта величина лежит в промежутке от 1/20 до 1/18, то есть расстояние до Солнца в 20 раз больше, чем до Луны



 — хорда для центрального угла α{displaystyle alpha }
— хорда для центрального угла α{displaystyle alpha } , d{displaystyle d}
, d{displaystyle d} — диаметр круга.
— диаметр круга. , и это облегчало вычисления. У Птолемея R=60 единиц. Согласно современным реконструкциям
, и это облегчало вычисления. У Птолемея R=60 единиц. Согласно современным реконструкциям
 (
(
 прямой)
прямой) (частный случай
(частный случай 
 (частный случай
(частный случай 
 (тоже вытекает из сферической теоремы косинусов)
(тоже вытекает из сферической теоремы косинусов)

 , cosnφ{displaystyle cos nvarphi }
, cosnφ{displaystyle cos nvarphi } для n=2,3,4,5{displaystyle n=2,3,4,5}
для n=2,3,4,5{displaystyle n=2,3,4,5} . В «Сурья-сиддханте» и в трудах Брахмагупты при решении задач фактически используется
. В «Сурья-сиддханте» и в трудах Брахмагупты при решении задач фактически используется 

 ), соответствующая современному выражению для дифференциала синуса. Опираясь на формулу синуса суммы, Бхаскара опубликовал более точные и подробные, чем у Ариабхаты, тригонометрические таблицы с шагом 1°
), соответствующая современному выражению для дифференциала синуса. Опираясь на формулу синуса суммы, Бхаскара опубликовал более точные и подробные, чем у Ариабхаты, тригонометрические таблицы с шагом 1°
 . Искусные методы для вычисления этой величины изобрели Ибн Юнис,
. Искусные методы для вычисления этой величины изобрели Ибн Юнис,  (все знаки верны). В составленных при его участии «Астрономических таблицах»
(все знаки верны). В составленных при его участии «Астрономических таблицах»  . В другом труде, «Геодезия», Бируни сообщил результаты собственных измерений длины земного
. В другом труде, «Геодезия», Бируни сообщил результаты собственных измерений длины земного 
 , чтобы табличные значения были представлены целыми числами (десятичные дроби вошли в обиход несколько позднее, причём мощным стимулом к их применению стали именно тригонометрические вычисления
, чтобы табличные значения были представлены целыми числами (десятичные дроби вошли в обиход несколько позднее, причём мощным стимулом к их применению стали именно тригонометрические вычисления ; его последователи в XVII веке сократили это обозначение до co-sinus (Эдмунд Гунтер)
; его последователи в XVII веке сократили это обозначение до co-sinus (Эдмунд Гунтер) и отношение противолежащих сторон a:b{displaystyle a:b}
и отношение противолежащих сторон a:b{displaystyle a:b} . Для решения Финке использовал
. Для решения Финке использовал 






 . Работы в области тригонометрии проводили такие крупные математики XVII века, как
. Работы в области тригонометрии проводили такие крупные математики XVII века, как  не может быть, вообще говоря, алгебраически выражен через x{displaystyle x}
не может быть, вообще говоря, алгебраически выражен через x{displaystyle x} , то есть, в современной терминологии, тригонометрические функции
, то есть, в современной терминологии, тригонометрические функции 
 сторонами при различных постановках задачи: заданы n−1{displaystyle ~n-1}
сторонами при различных постановках задачи: заданы n−1{displaystyle ~n-1} сторона и n−2{displaystyle ~n-2}
сторона и n−2{displaystyle ~n-2} угла, или все углы и n−2{displaystyle ~n-2}
угла, или все углы и n−2{displaystyle ~n-2} угла
угла , но они не прижились
, но они не прижились
 и т. д. стали рассматриваться как безразмерные
и т. д. стали рассматриваться как безразмерные 
 в ряд:
в ряд:

