Локально тривиальное расслоение — расслоение, которое локально выглядит как прямое произведение.
Содержание
Определение
Локально тривиальным расслоение пространства E{displaystyle E}
над базой B{displaystyle B} со слоем F{displaystyle F} называется непрерывное сюръективное отображение π:E→B{displaystyle pi :Eto B} , такое что для всякой точки базы x∈B{displaystyle xin B} существует окрестность U{displaystyle U} , над которой расслоение устроено как тривиальное, то есть существует гомеоморфизм φ{displaystyle varphi } открытого множества π−1(U){displaystyle pi ^{-1}(U)} на пространство U×F{displaystyle Utimes F} , преобразующее отображение π{displaystyle pi } в проекцию proj1:U×F→U{displaystyle mathrm {proj_{1}} :,Utimes Fto U} , так что коммутативна диаграмма
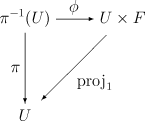 ,
,
Связанные определения
- Пространство E{displaystyle E} называется (тотальным) пространством расслоения или расслоенным пространством,
- Пространство B{displaystyle B} называется базой расслоения,
- Множество Fx=π−1{x}{displaystyle F_{x}=pi ^{-1}{x}} называется слоем расслоения π{displaystyle pi } над точкой x∈B{displaystyle xin B} . Каждый слой гомеоморфен пространству F{displaystyle F} , поэтому пространство F{displaystyle F} называется общим (или модельным) слоем расслоения π{displaystyle pi } ,
- Гомеоморфизм φ{displaystyle varphi } , отождествляющий ограничение расслоения π{displaystyle pi } над окрестностью точки x{displaystyle x} с некоторым тривиальным расслоением, называется локальной тривиализацией расслоения π{displaystyle pi } над окрестностью точки x{displaystyle x} .
- Если {Uα}{displaystyle {U_{alpha }}} — покрытие базы B{displaystyle B} открытыми множествами, и φα:π−1(Uα)→Uα×F{displaystyle varphi _{alpha }:pi ^{-1}(U_{alpha })to U_{alpha }times F} — соответствующие им отображения тривиализации, тогда семейство {(Uα,φα)}{displaystyle {(U_{alpha },varphi _{alpha })}} называется тривиализующим атласом расслоения π:E→B{displaystyle pi :Eto B} .
- Предположим локально тривиальное расслоение π:E→B{displaystyle pi :Eto B} снабжено покрытием {Uα}{displaystyle {U_{alpha }}} базы B{displaystyle B} с выделенной тривиализацией ϕα:Uα×F→π−1(Uα){displaystyle phi _{alpha }:U_{alpha }times Fto pi ^{-1}(U_{alpha })} и сужение любого отображения сличения ϕα−1∘ϕβ{displaystyle phi _{alpha }^{-1}circ phi _{beta }} на слой принадлежит некоторой подгруппе G{displaystyle G} группы всех гомеоморфизмов F{displaystyle F} . Тогда π{displaystyle pi } называется локально тривиальным расслоением со структурной группой G{displaystyle G} .
Примеры
- Тривиальное расслоение, то есть проекция на фактор B×F→B{displaystyle Btimes Fto B}
- Накрытие
- Касательное, кокасательное и тензорные расслоения над произвольным многообразием локально тривиальны.
- Лист Мёбиуса — пространство не тривиального расслоения над окружностью.
- Сконструировать расслоение можно, задав произвольно его базу (пространство B{displaystyle B} ), общий слой (пространство F{displaystyle F} ) и отображения перехода (1-коцикл Чеха {uαβ:Uα→AutF}{displaystyle {u_{alpha beta }:U_{alpha }to mathrm {Aut} ,F}} ) для какого-нибудь открытого покрытия пространства B{displaystyle B} . Тогда пространство E формально можно получить как множество троек вида {(α,x,fα):x∈Uα,fα∈F}{displaystyle {(alpha ,x,f_{alpha }):,xin U_{alpha },,f_{alpha }in F}} с правилом отождествления:
- (α,x,fα)=(β,x,fβ){displaystyle (alpha ,x,f_{alpha })=(beta ,x,f_{beta })} , если fβ=uβαfα{displaystyle f_{beta }=u_{beta alpha }f_{alpha }}
- Если на пространстве E{displaystyle E} задано непрерывное свободное действие группы G{displaystyle G} , то естественное отображение E→E/G{displaystyle Eto E/G} является локально тривиальным расслоением. Расслоения такого типа называются главными.
Свойства
- Отображения перехода удовлетворяют условию 1-коцикла Чеха:
- Если x∈Uα∩Uβ∩Uγ{displaystyle xin U_{alpha }cap U_{beta }cap U_{gamma }} , то uβα(x)=uβγ(x)∘uγα(x){displaystyle u_{beta alpha }(x)=u_{beta gamma }(x)circ u_{gamma alpha }(x)} .
- Два расслоения над одной и той же базой и с одним и тем же общим слоем изоморфны, тогда и только тогда, когда 1-коциклы Чеха, соответствующие им, когомологичны. (Отметим, что в случае, когда группа AutF{displaystyle mathrm {Aut} ,F} некоммутативна, одномерные когомологии H1(B,AutF){displaystyle H^{1}(B,mathrm {Aut} ,F)} не образуют группу, а образуют множество, на котором действует (слева) группа 0-коцепей Чеха C0(B,AutF){displaystyle C^{0}(B,mathrm {Aut} ,F)} :
- uαβ′(x)=fα(x)∘uαβ(x)∘fβ(x)−1{displaystyle u_{alpha beta }'(x)=f_{alpha }(x)circ u_{alpha beta }(x)circ f_{beta }(x)^{-1}} ,
- где {fα:Uα→AutF}{displaystyle {f_{alpha }:U_{alpha }to mathrm {Aut} ,F}} — 0-коцепь Чеха, действующая на 1-коцикл Чеха {uαβ:Uα∩Uβ→AutF}{displaystyle {u_{alpha beta }:U_{alpha }cap U_{beta }to mathrm {Aut} ,F}} . 1-коциклы называются когомологичными, если они лежат в одной орбите этого действия.)
- Для любого локально тривиального расслоения π:X→B{displaystyle pi :Xto B} и непрерывного отображения f:B′→B{displaystyle f:B’to B} индуцированное расслоение f∗(π){displaystyle f^{*}(pi )} является локально тривиальным.
Вариации и обобщения
- Локально тривиальные расслоения являются частным случаем
- Если пространства E,B,F{displaystyle E,B,F} — гладкие (дифференцируемые) многообразия, отображение π{displaystyle pi } — гладкое и допускающее тривиализующий атлас с гладкими отображениями тривиализации, то само расслоение называется гладким.
- Расслоение называется голоморфным, если пространства E,B,F{displaystyle E,B,F} — комплексные многообразия, отображение π{displaystyle pi } — голоморфное и существует тривиализующий атлас с голоморфными отображениями тривиализации.
Литература
- Васильев В. А. Введение в топологию. — М.: ФАЗИС, 1997. — 132 с. — ISBN 5-7036-0036-7.
| Это статья-заготовка по топологии. Помогите Википедии, дополнив эту статью, как и любую другую. |

 над базой B{displaystyle B}
над базой B{displaystyle B} со слоем F{displaystyle F}
со слоем F{displaystyle F} называется непрерывное сюръективное отображение π:E→B{displaystyle pi :Eto B}
называется непрерывное сюръективное отображение π:E→B{displaystyle pi :Eto B} , такое что для всякой точки базы x∈B{displaystyle xin B}
, такое что для всякой точки базы x∈B{displaystyle xin B} существует окрестность U{displaystyle U}
существует окрестность U{displaystyle U} , над которой расслоение устроено как тривиальное, то есть существует
, над которой расслоение устроено как тривиальное, то есть существует  открытого множества π−1(U){displaystyle pi ^{-1}(U)}
открытого множества π−1(U){displaystyle pi ^{-1}(U)} на пространство U×F{displaystyle Utimes F}
на пространство U×F{displaystyle Utimes F} , преобразующее отображение π{displaystyle pi }
, преобразующее отображение π{displaystyle pi } в проекцию proj1:U×F→U{displaystyle mathrm {proj_{1}} :,Utimes Fto U}
в проекцию proj1:U×F→U{displaystyle mathrm {proj_{1}} :,Utimes Fto U} , так что
, так что  называется слоем расслоения π{displaystyle pi }
называется слоем расслоения π{displaystyle pi } с некоторым тривиальным расслоением, называется локальной тривиализацией расслоения π{displaystyle pi }
с некоторым тривиальным расслоением, называется локальной тривиализацией расслоения π{displaystyle pi } — покрытие базы B{displaystyle B}
— покрытие базы B{displaystyle B} — соответствующие им отображения тривиализации, тогда семейство {(Uα,φα)}{displaystyle {(U_{alpha },varphi _{alpha })}}
— соответствующие им отображения тривиализации, тогда семейство {(Uα,φα)}{displaystyle {(U_{alpha },varphi _{alpha })}} называется тривиализующим атласом расслоения π:E→B{displaystyle pi :Eto B}
называется тривиализующим атласом расслоения π:E→B{displaystyle pi :Eto B} и сужение любого отображения сличения ϕα−1∘ϕβ{displaystyle phi _{alpha }^{-1}circ phi _{beta }}
и сужение любого отображения сличения ϕα−1∘ϕβ{displaystyle phi _{alpha }^{-1}circ phi _{beta }} на слой принадлежит некоторой подгруппе G{displaystyle G}
на слой принадлежит некоторой подгруппе G{displaystyle G} группы всех гомеоморфизмов F{displaystyle F}
группы всех гомеоморфизмов F{displaystyle F}
 ) для какого-нибудь открытого покрытия пространства B{displaystyle B}
) для какого-нибудь открытого покрытия пространства B{displaystyle B} с правилом отождествления:
с правилом отождествления: , если fβ=uβαfα{displaystyle f_{beta }=u_{beta alpha }f_{alpha }}
, если fβ=uβαfα{displaystyle f_{beta }=u_{beta alpha }f_{alpha }}
 является локально тривиальным расслоением. Расслоения такого типа называются главными.
является локально тривиальным расслоением. Расслоения такого типа называются главными. , то uβα(x)=uβγ(x)∘uγα(x){displaystyle u_{beta alpha }(x)=u_{beta gamma }(x)circ u_{gamma alpha }(x)}
, то uβα(x)=uβγ(x)∘uγα(x){displaystyle u_{beta alpha }(x)=u_{beta gamma }(x)circ u_{gamma alpha }(x)} .
. некоммутативна, одномерные
некоммутативна, одномерные  не образуют
не образуют  :
:
 ,
, — 0-коцепь Чеха, действующая на 1-коцикл Чеха {uαβ:Uα∩Uβ→AutF}{displaystyle {u_{alpha beta }:U_{alpha }cap U_{beta }to mathrm {Aut} ,F}}
— 0-коцепь Чеха, действующая на 1-коцикл Чеха {uαβ:Uα∩Uβ→AutF}{displaystyle {u_{alpha beta }:U_{alpha }cap U_{beta }to mathrm {Aut} ,F}} . 1-коциклы называются когомологичными, если они лежат в одной орбите этого действия.)
. 1-коциклы называются когомологичными, если они лежат в одной орбите этого действия.) и непрерывного отображения f:B′→B{displaystyle f:B’to B}
и непрерывного отображения f:B′→B{displaystyle f:B’to B}
 является локально тривиальным.
является локально тривиальным. — гладкие (дифференцируемые)
— гладкие (дифференцируемые) 