Дифференциальная геометрия кривых — раздел дифференциальной геометрии, который занимается исследованием гладких пространственных и плоских кривых в евклидовом пространстве аналитическими методами.
Содержание
- 1 Способы задания кривой
- 2 Соприкосновение
- 3 Длина дуги кривой
- 4 Кривизна
- 5 Кручение
- 6 Формулы Френе
- 7 Натуральные уравнения кривой
- 8 Примечания
- 9 См. также
- 10 Литература
Способы задания кривой
Наиболее общий способ задать уравнение пространственной кривой — параметрический:
| x=x(t),y=y(t),z=z(t){displaystyle x=x(t),quad y=y(t),quad z=z(t)qquad qquad } | ((1),) |
где x(t), y(t), z(t){displaystyle x(t), y(t), z(t)}
— гладкие функции параметра t{displaystyle t} , причем (x′)2+(y′)2+(z′)2 >0{displaystyle (x’)^{2}+(y’)^{2}+(z’)^{2} >0} (условие регулярности).
Часто удобно использовать инвариантную и компактную запись уравнения кривой с помощью вектор-функции:
- r=r(t){displaystyle mathbf {r} =mathbf {r} (t)} ,
где в левой части стоит радиус-вектор точек кривой, а правая определяет его зависимость от некоторого параметра t{displaystyle t}
. Раскрыв эту запись в координатах, мы получаем формулу (1).
В зависимости от свойств дифференцируемости функций x(t), y(t), z(t){displaystyle x(t), y(t), z(t)}
, задающих кривую, говорят о степени гладкости (регулярности) кривой. Кривая называется регулярной, если для любой её точки, при подходящем выборе прямоугольной декартовой системы координат x, y, z{displaystyle x, y, z} , она допускает в окрестности этой точки задание уравнениями вида:
- y=y(x), z=z(x){displaystyle y=y(x), z=z(x)} ,
где y(x) {displaystyle y(x) }
и z(x) {displaystyle z(x) } — дифференцируемые функции.
Для того чтобы точка кривой, заданной общим уравнением (1), была обыкновенной (не особой точкой), достаточно, чтобы в этой точке выполнялось вышеуказанное неравенство
- (x′)2+(y′)2+(z′)2 >0.{displaystyle (x’)^{2}+(y’)^{2}+(z’)^{2} >0.}
Дифференциальная геометрия рассматривает также кусочно-гладкие кривые, которые состоят из гладких участков, разделённых особыми точками. В особых точках определяющие функции либо не удовлетворяют условиям регулярности, либо вообще не дифференцируемы.
Плоские кривые
Важный класс кривых представляют плоские кривые, то есть кривые, лежащие в плоскости. Плоскую кривую также можно задать параметрически, первыми двумя из трёх уравнений (1). Другие способы:
- Явное задание: y=f(x) {displaystyle y=f(x) } .
- Неявное задание: F(x, y)=0{displaystyle F(x, y)=0} .
Функции f, F{displaystyle f, F}
предполагаются непрерывно дифференцируемыми. При неявном задании точка кривой будет обыкновенной, если в её окрестности функция F(x,y) {displaystyle F(x,y) } имеет непрерывные частные производные Fx′, Fy′{displaystyle F_{x}’, F_{y}’} , не равные нулю одновременно. Полукубическая парабола
Полукубическая парабола
Приведём примеры особых точек для плоских кривых.
- Полукубическая парабола: x=t2; y=at3.{displaystyle x=t^{2}; y=at^{3}.} Обе производные равны нулю в начале координат. Это особая точка (точка возврата первого рода), в ней вектор касательной скачкообразно меняет направление на противоположное.
- Уравнение (x−1)(x2+y2) =0{displaystyle (x-1)(x^{2}+y^{2}) =0} определяет кривую, состоящую из прямой x=1 {displaystyle x=1 } и изолированной особой точки в начале координат.
- Лемниската Бернулли — особая точка при самопересечении. В особой точке функция дифференцируема, однако условие регулярности нарушено.
Соприкосновение
Ряд основных понятий теории кривых вводится с помощью понятия соприкосновения множеств,которое состоит в следующем.Пусть M{displaystyle M}
и m{displaystyle m} — два множества с общей точкой O{displaystyle O} .Говорят, что множество M{displaystyle M} имеет с m{displaystyle m} в точке O{displaystyle O} соприкосновение порядка α⩾1{displaystyle alpha geqslant 1} , если
- δ(X)|XO|α→0{displaystyle {frac {delta (X)}{left|XOright|^{alpha }}}to 0} при X→O{displaystyle Xto O} ,
где δ(X){displaystyle delta (X)}
— расстояние точки X{displaystyle X} множества M{displaystyle M} от m{displaystyle m} .
В применении к кривым это означает следующее: две кривые в общей точке имеют степень касания не ниже k-го порядка, если их производные в общей точке, до k-го порядка включительно, совпадают.
Касательная
Основная статья: Касательная прямая Рис. 1. В точке кривой построены векторы касательной (T), главной нормали (N) и бинормали (B). Показана также соприкасающаяся плоскость, содержащая касательную и главную нормаль.
Рис. 1. В точке кривой построены векторы касательной (T), главной нормали (N) и бинормали (B). Показана также соприкасающаяся плоскость, содержащая касательную и главную нормаль.
Если в качестве M{displaystyle M}
взять кривую, а в качестве m{displaystyle m} прямую, проходящую через точку O{displaystyle O} кривой, то при α⩾1{displaystyle alpha geqslant 1} условие соприкосновения определяет касательную к кривой в точке O{displaystyle O} (рис. 1). Касательная в точке P{displaystyle P} кривой также может быть определена как предельное положение секущей, проходящей через P{displaystyle P} и близкую к ней точку P1{displaystyle P_{1}} , когда P1{displaystyle P_{1}} стремится к P{displaystyle P} .
Гладкая регулярная кривая в каждой точке имеет определённую касательную. Направление касательной в точке t0{displaystyle t_{0}}
кривой, задаваемой уравнениями (1), совпадает с направлением вектора {x′(t0), y′(t0), z′(t0)}{displaystyle {x'(t_{0}), y'(t_{0}), z'(t_{0})}} . В векторной записи это производная drdt(t0){displaystyle {frac {dmathbf {r} }{dt}}(t_{0})} .
В дифференциальной геометрии выводятся уравнения касательной для различных способов аналитического задания кривой. В частности, для кривой, задаваемой уравнениями (1), уравнения касательной в точке, отвечающей значению параметра t0{displaystyle t_{0}}
, будут
- X−x0x0′=Y−y0y0′=Z−z0z0′{displaystyle {frac {X-x_{0}}{x_{0}’}}={frac {Y-y_{0}}{y_{0}’}}={frac {Z-z_{0}}{z_{0}’}}} ,
где индекс 0 {displaystyle {}_{0} }
указывает на значение функций x,y,z {displaystyle x,y,z } и их производных в точке t0 {displaystyle t_{0} } .
Для плоской кривой уравнение касательной в точке (x0, y0){displaystyle (x_{0}, y_{0})}
имеет следующий вид.
- Параметрическое задание: Y=y0+y0′x0′(X−x0){displaystyle Y=y_{0}+{frac {y_{0}’}{x_{0}’}}(X-x_{0})}
- Явное задание: Y=y0+f0′(X−x0) {displaystyle Y=y_{0}+f_{0}'(X-x_{0}) }
- Неявное задание: Y=y0−(Fx′)0(Fy′)0(X−x0){displaystyle Y=y_{0}-{frac {(F_{x}’)_{0}}{(F_{y}’)_{0}}}(X-x_{0})}
Соприкасающаяся плоскость и нормали
Если взять в качестве m{displaystyle m}
плоскость, проходящую через точку O{displaystyle O} кривой M{displaystyle M} , то условие соприкосновения при α⩾2{displaystyle alpha geqslant 2} определяет соприкасающуюся плоскость кривой (рис. 1).Дважды дифференцируемая кривая в каждой точке имеет соприкасающуюся плоскость.Она либо единственная, либо любая плоскость, проходящая через касательную кривой, является соприкасающейся.
Пусть r=r(t){displaystyle mathbf {r} =mathbf {r} (t)}
— уравнение кривой. Тогда уравнение R=R(X,Y,Z){displaystyle mathbf {R} =mathbf {R} (X,Y,Z)} её соприкасающейся плоскости определяется из соотношения:
- (R−r,r′,r″)=0{displaystyle (mathbf {R} -mathbf {r} ,mathbf {r} ‘,mathbf {r} »)=0}
В координатах оно имеет вид:
- |X−xY−yZ−zx′y′z′x″y″z″|=0{displaystyle {begin{vmatrix}X-x&Y-y&Z-zx’&y’&z’x»&y»&z»end{vmatrix}}=0}
Прямая, перпендикулярная касательной и проходящая через точку касания, называется нормалью к кривой. Плоскость, перпендикулярная касательной в данной точке кривой, называется нормальной плоскостью; все нормали для данной точки лежат в нормальной плоскости. Нормаль, лежащую в соприкасающейся плоскости, называют главной нормалью, а нормаль, перпендикулярная соприкасающейся плоскости, называется бинормалью. Также нормалью и бинормалью для краткости могут называть единичные векторы вдоль этих прямых (при этом направление вектора главной нормали обычно выбирают совпадающим с направлением вектора кривизны кривой[1]).
Векторное уравнение бинормали в точке, отвечающей значению t0{displaystyle t_{0}}
параметра t{displaystyle t} , имеет вид:
- r(λ)=r(t0)+λ[r′(t0), r″(t0)].{displaystyle {boldsymbol {r}}(lambda )={boldsymbol {r}}(t_{0})+lambda [{boldsymbol {r}}'(t_{0}),~{boldsymbol {r}}»(t_{0})].}
Направление главной нормали может быть получено как двойное векторное произведение: [r′ [r′ r″]]{displaystyle [mathbf {r} ‘ [mathbf {r} ‘ mathbf {r} »]]}
.
Для плоской кривой содержащая её плоскость совпадает с соприкасающейся. Нормаль, с точностью до знака, только одна — главная, и её уравнение в точке (x0, y0){displaystyle (x_{0}, y_{0})}
имеет следующий вид.
- Параметрическое задание: Y=y0−x0′y0′(X−x0){displaystyle Y=y_{0}-{frac {x_{0}’}{y_{0}’}}(X-x_{0})}
- Явное задание: Y=y0−X−x0f0′{displaystyle Y=y_{0}-{frac {X-x_{0}}{f_{0}’}}}
- Неявное задание: Y=y0+(Fy′)0(Fx′)0(X−x0){displaystyle Y=y_{0}+{frac {(F_{y}’)_{0}}{(F_{x}’)_{0}}}(X-x_{0})}
Соприкасающаяся окружность
Основная статья: Соприкасающаяся окружность Рис. 2. Соприкасающаяся окружность в точке кривой
Рис. 2. Соприкасающаяся окружность в точке кривой
Окружность, соприкасающаяся с кривой в заданной точке P{displaystyle P}
, имеет с кривой соприкосновение порядка α⩾2{displaystyle alpha geqslant 2} (рис. 2). Она существует в каждой точке дважды дифференцируемой кривой с отличной от нуля кривизной (см. ниже) и является также пределом окружности, проходящей через P{displaystyle P} и две близкие к ней точки P1, P2{displaystyle P_{1}, P_{2}} , когда P1, P2{displaystyle P_{1}, P_{2}} стремятся к P{displaystyle P} .
Центр соприкасающейся окружности называют центром кривизны, а радиус — радиусом кривизны. Радиус кривизны является величиной, обратной кривизне (см. ниже). Центр соприкасающейся окружности всегда лежит на главной нормали; отсюда следует, что эта нормаль всегда направлена в сторону вогнутости кривой.
Геометрическое место центров кривизны кривой называется эволютой. Кривая, ортогонально пересекающая касательные кривой, называется эвольвентой. Построение эволюты и эвольвенты — взаимно обратные операции, то есть для эвольвенты данной кривой эволютой является сама кривая.
Длина дуги кривой
Основная статья: Длина кривой Рис. 3. Полигональное приближение кривой
Рис. 3. Полигональное приближение кривой
Для измерения длины участка (дуги) произвольной кривой эта кривая заменяется ломаной, содержащей точки кривой как точки излома, и максимум длин всех таких ломаных принимается за длину кривой (рис. 3). В инвариантном виде формула для вычисления длины дуги (спрямления кривой) имеет вид:
- s=∫t1t2|r′(t)|dt{displaystyle s=int limits _{t_{1}}^{t_{2}}|mathbf {r’} (t)|,dt}
То же в декартовых координатах:
- s=∫t1t2(x′(t))2+(y′(t))2+(z′(t))2dt.{displaystyle s=int limits _{t_{1}}^{t_{2}}{sqrt {(x'(t))^{2}+(y'(t))^{2}+(z'(t))^{2}}},dt.}
В полярных координатах для плоской кривой:
- s=∫abr2+(drdθ)2dθ.{displaystyle s=int limits _{a}^{b}{sqrt {r^{2}+left({frac {dr}{dtheta }}right)^{2}}},dtheta .}
Параметризация
Кривая допускает бесчисленное множество различных способов параметрического задания уравнениями вида (1). Среди них особое значение имеет так называемая естественная параметризация, когда параметром служит длина дуги кривой, отсчитываемая от некоторой фиксированной точки.
Среди преимуществ такой параметризации:
- r′{displaystyle mathbf {r} ‘} имеет единичную длину и поэтому совпадает с ортом касательной.
- r″{displaystyle mathbf {r} »} по длине совпадает с кривизной, а по направлению — с главной нормалью.
Кривизна
При движении вдоль кривой её касательная меняет направление. Скорость этого вращения (отношение угла поворота касательной за бесконечно малый промежуток времени к этому промежутку) при равномерном, с единичной скоростью, движении вдоль кривой называется кривизной кривой. Производная же по времени положительного единичного вектора касательной называется в этом случае вектором кривизны кривой. То и другое — функции точки кривой. Кривизна есть абсолютная величина вектора кривизны.
В случае произвольного параметрического задания кривой[2] кривизна кривой в трехмерном пространстве определяется по формуле
- k1=|[r′(t), r″(t)]||r′(t)|3{displaystyle k_{1}={frac {left|[mathbf {r} ‘(t), mathbf {r} »(t)]right|}{left|mathbf {r} ‘(t)right|^{3}}}} ,
где r(t){displaystyle mathbf {r} (t)}
— вектор-функция с координатами x(t), y(t), z(t){displaystyle x(t), y(t), z(t)} .
В координатах:
- k1=(z″y′−y″z′)2+(x″z′−z″x′)2+(y″x′−x″y′)2(x′2+y′2+z′2)3/2{displaystyle k_{1}={frac {sqrt {(z»y’-y»z’)^{2}+(x»z’-z»x’)^{2}+(y»x’-x»y’)^{2}}}{(x’^{2}+y’^{2}+z’^{2})^{3/2}}}}
Для кривой в более многомерном пространстве можно заменить векторное произведение, обозначенное здесь квадратными скобками, на внешнее произведение.
Также для кривой в любой размерности пространства можно воспользоваться формулой вектора кривизны:
- k=dτdl{displaystyle mathbf {k} ={frac {dmathbf {tau } }{dl}}}
и фактом, что кривизна есть его модуль, а также выражением для единичного вектора касательной
- τ=drdl=r′|r′|{displaystyle mathbf {tau } ={frac {dmathbf {r} }{dl}}={frac {r’}{|r’|}}}
и
- dl=|r′|dt,{displaystyle dl=|mathbf {r} ‘|dt,}
и получить для кривизны формулу:
- k=|1|r′|(r′|r′|)′|,{displaystyle k=left|{frac {1}{|mathbf {r} ‘|}}left({frac {mathbf {r} ‘}{|mathbf {r} ‘|}}right)’right|,}
или, раскрыв скобки:
- k=|r″(r′)2−r′(r″,r′)(r′)4|.{displaystyle k=left|{frac {mathbf {r} »}{(mathbf {r} ‘)^{2}}}-mathbf {r} ‘{frac {(mathbf {r} »,mathbf {r} ‘)}{(mathbf {r} ‘)^{4}}}right|.}
Прямые и только прямые имеют всюду равную нулю кривизну. Поэтому кривизна наглядно показывает, насколько (в данной точке) кривая отличается от прямой линии: чем ближе кривизна к нулю, тем это отличие меньше. Кривизна окружности радиуса R{displaystyle R}
равна 1/R{displaystyle 1/R} .
Дважды дифференцируемая кривая в каждой точке, где кривизна отлична от нуля, имеет единственную соприкасающуюся плоскость.
Для плоских кривых можно различать направление вращения касательной при движении вдоль кривой, поэтому кривизне можно приписывать знак в зависимости от направления этого вращения. Кривизна плоской кривой, задаваемой уравнениями x=x(t), y=y(t){displaystyle x=x(t), y=y(t)}
, определяется по формуле
- k=±y″x′−x″y′(x′2+y′2)3/2{displaystyle k=pm {frac {y»x’-x»y’}{(x’^{2}+y’^{2})^{3/2}}}} .
Знак +{displaystyle +}
или −{displaystyle -} берётся по соглашению, но сохраняется вдоль всей кривой.
Кручение
При движении вдоль кривой в окрестности заданной точки соприкасающаяся плоскость вращается, причём касательная к кривой является мгновенной осью этого вращения. Скорость вращения соприкасающейся плоскости при равномерном, с единичной скоростью, движении называется кручением. Направление вращения определяет знак кручения.
Трижды дифференцируемая кривая в каждой точке с отличной от нуля кривизной имеет определённое кручение. В случае параметрического задания кривой уравнениями (1) кручение кривой определяется по формуле
- k2=(r′,r″,r‴)|[r′, r″]|2,{displaystyle k_{2}={frac {(mathbf {r} ‘,mathbf {r} »,mathbf {r} »’)}{left|[mathbf {r} ‘, mathbf {r} »]right|^{2}}},}
здесь (∗,∗,∗){displaystyle (*,*,*)}
обозначает смешанное произведение. В координатах:
- k2=z‴(x′y″−y′x″)+z″(x‴y′−x′y‴)+z′(x″y‴−x‴y″)(x′2+y′2+z′2)(x″2+y″2+z″2).{displaystyle k_{2}={frac {z»'(x’y»-y’x»)+z»(x»’y’-x’y»’)+z'(x»y»’-x»’y»)}{(x’^{2}+y’^{2}+z’^{2})(x»^{2}+y»^{2}+z»^{2})}}.}
Для прямой кручение не определено, поскольку неоднозначно определяется соприкасающаяся плоскость. Плоская кривая в каждой точке имеет кручение, равное нулю. Обратно, кривая с тождественно равным нулю кручением — плоская.
Формулы Френе
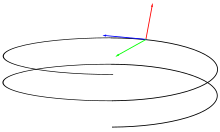 касательная главная нормаль бинормаль Рис. 4. Трёхгранник Френе для винтовой линии.
касательная главная нормаль бинормаль Рис. 4. Трёхгранник Френе для винтовой линии.
Фигура, составленная из касательной, главной нормали и бинормали, а также из трех плоскостей, попарно содержащих эти прямые, называют естественным трёхгранником (трёхгранником Френе, см. рис. 4). Соприкасающаяся и нормальная плоскости уже упоминались; третья плоскость, содержащая касательную и бинормаль, называется спрямляющей.
Если рёбра естественного трёхгранника в данной точке кривой принять за оси прямоугольной декартовой системы координат, то уравнение кривой в естественной параметризации раскладывается в окрестности этой точки в ряд по координате вдоль кривой:
- x=s+…,y=k12s2+…,z=−k1k26s3+……,{displaystyle x=s+dots ,y={frac {k_{1}}{2}}s^{2}+dots ,z=-{frac {k_{1}k_{2}}{6}}s^{3}+dots …,}
где k1 {displaystyle k_{1} }
и k2 {displaystyle k_{2} } — кривизна и кручение кривой в указанной точке.
Единичные векторы t→, n→, b→{displaystyle {boldsymbol {vec {t}}}, {boldsymbol {vec {n}}}, {boldsymbol {vec {b}}}}
, соответственно для касательной, главной нормали и бинормали кривой, при движении вдоль кривой изменяются.При соответствующем выборе направления этих векторов из определения кривизны и кручения получаются формулы:
| dt→ds=k1n→{displaystyle {frac {d{boldsymbol {vec {t}}}}{ds}}=k_{1}{boldsymbol {vec {n}}}} | ((2)) |
| dn→ds=−k1t→+k2b→{displaystyle {frac {d{boldsymbol {vec {n}}}}{ds}}=-k_{1}{boldsymbol {vec {t}}}+k_{2}{boldsymbol {vec {b}}}qquad } |
| db→ds=−k2n→{displaystyle {frac {d{boldsymbol {vec {b}}}}{ds}}=-k_{2}{boldsymbol {vec {n}}}} |
где дифференцирование идёт по дуге кривой. Указанные выше формулы называют формулами Френе́, или Френе-Серре.
Кинематическое истолкование
Будем рассматривать длину дуги заданной кривой как время, а трёхгранник Френе — как твёрдое тело, движущееся вдоль кривой. Тогда это движение в каждый момент времени состоит из поступательного (вдоль касательной) и мгновенного вращения с угловой скоростью ω→{displaystyle {boldsymbol {vec {omega }}}}
(вектор Дарбу). Из формул Френе вытекает:
- ω→=k1 b→+k2 t→{displaystyle {boldsymbol {vec {omega }}}=k_{1} {boldsymbol {vec {b}}}+k_{2} {boldsymbol {vec {t}}}}
Это означает, что вектор мгновенного вращения лежит в спрямляющей плоскости и распадается на 2 составляющие: вращение вокруг бинормали со скоростью k1 {displaystyle k_{1} }
(поворот) и вращение вокруг касательной со скоростью k2 {displaystyle k_{2} } (кручение).
Натуральные уравнения кривой
Кривая с отличной от нуля кривизной полностью определяется (с точностью до положения в пространстве) заданием её кривизны и кручения как функций дуги s{displaystyle s}
кривой. В связи с этим систему уравнения
- k1=k1(s), k2=k2(s){displaystyle k_{1}=k_{1}(s),~~k_{2}=k_{2}(s)}
называют натуральными уравнениями кривой.
Пример
Рассмотрим винтовую линию (рис. 4), заданную уравнениями:
- x(t)=a cost{displaystyle x(t)=a cos t}
- y(t)=a sint{displaystyle y(t)=a sin t}
- z(t)=b t{displaystyle z(t)=b t}
По вышеприведенным формулам получаем:
- k1=aa2+b2{displaystyle k_{1}={frac {a}{a^{2}+b^{2}}}}
- k2=ba2+b2{displaystyle k_{2}={frac {b}{a^{2}+b^{2}}}}
Таким образом, кривизна и кручение винтовой линии постоянны. Поскольку натуральные уравнения однозначно определяют форму кривой, других кривых с постоянными кривизной и кручением не существует. Предельными случаями винтовой линии являются окружность (она получается при b=0 {displaystyle b=0 }
) и прямая ( a=0 {displaystyle a=0 } ).
Примечания
- ↑ Плоскость, соприкасающаяся с кривой в данной точке, таким образом, есть плоскость, в которой лежат касательный вектор и вектор кривизны, полагая, что каждый из этих векторов имеет начало в данной точке кривой.
- ↑ Т.е. при движении вдоль кривой вообще говоря не с постоянной скоростью по мере роста параметра t.
См. также
Литература
- Погорелов А. И. Дифференциальная геометрия (6-е издание). М.: Наука, 1974.
- Рашевский П. К. Курс дифференциальной геометрии (3-е издание). М.-Л.: ГИТТЛ, 1950.


 — гладкие функции параметра t{displaystyle t}
— гладкие функции параметра t{displaystyle t} , причем (x′)2+(y′)2+(z′)2 >0{displaystyle (x’)^{2}+(y’)^{2}+(z’)^{2} >0}
, причем (x′)2+(y′)2+(z′)2 >0{displaystyle (x’)^{2}+(y’)^{2}+(z’)^{2} >0} (условие регулярности).
(условие регулярности). ,
, , она допускает в окрестности этой точки задание уравнениями вида:
, она допускает в окрестности этой точки задание уравнениями вида: ,
, и z(x) {displaystyle z(x) }
и z(x) {displaystyle z(x) } — дифференцируемые функции.
— дифференцируемые функции.
 .
. .
. предполагаются непрерывно дифференцируемыми. При неявном задании точка кривой будет обыкновенной, если в её окрестности функция F(x,y) {displaystyle F(x,y) }
предполагаются непрерывно дифференцируемыми. При неявном задании точка кривой будет обыкновенной, если в её окрестности функция F(x,y) {displaystyle F(x,y) } имеет непрерывные частные производные Fx′, Fy′{displaystyle F_{x}’, F_{y}’}
имеет непрерывные частные производные Fx′, Fy′{displaystyle F_{x}’, F_{y}’} , не равные нулю одновременно.
, не равные нулю одновременно. Обе производные равны нулю в начале координат. Это особая точка (точка возврата первого рода), в ней вектор касательной скачкообразно меняет направление на противоположное.
Обе производные равны нулю в начале координат. Это особая точка (точка возврата первого рода), в ней вектор касательной скачкообразно меняет направление на противоположное. определяет кривую, состоящую из прямой x=1 {displaystyle x=1 }
определяет кривую, состоящую из прямой x=1 {displaystyle x=1 } и изолированной особой точки в начале координат.
и изолированной особой точки в начале координат.
 и m{displaystyle m}
и m{displaystyle m} — два множества с общей точкой O{displaystyle O}
— два множества с общей точкой O{displaystyle O} .Говорят, что множество M{displaystyle M}
.Говорят, что множество M{displaystyle M} , если
, если при X→O{displaystyle Xto O}
при X→O{displaystyle Xto O} ,
, — расстояние точки X{displaystyle X}
— расстояние точки X{displaystyle X} множества M{displaystyle M}
множества M{displaystyle M} кривой также может быть определена как предельное положение секущей, проходящей через P{displaystyle P}
кривой также может быть определена как предельное положение секущей, проходящей через P{displaystyle P} , когда P1{displaystyle P_{1}}
, когда P1{displaystyle P_{1}} кривой, задаваемой уравнениями (1), совпадает с направлением вектора {x′(t0), y′(t0), z′(t0)}{displaystyle {x'(t_{0}), y'(t_{0}), z'(t_{0})}}
кривой, задаваемой уравнениями (1), совпадает с направлением вектора {x′(t0), y′(t0), z′(t0)}{displaystyle {x'(t_{0}), y'(t_{0}), z'(t_{0})}} . В векторной записи это производная drdt(t0){displaystyle {frac {dmathbf {r} }{dt}}(t_{0})}
. В векторной записи это производная drdt(t0){displaystyle {frac {dmathbf {r} }{dt}}(t_{0})} .
. ,
, указывает на значение функций x,y,z {displaystyle x,y,z }
указывает на значение функций x,y,z {displaystyle x,y,z } и их производных в точке t0 {displaystyle t_{0} }
и их производных в точке t0 {displaystyle t_{0} } .
. имеет следующий вид.
имеет следующий вид.


 определяет соприкасающуюся плоскость кривой (рис. 1).Дважды дифференцируемая кривая в каждой точке имеет соприкасающуюся плоскость.Она либо единственная, либо любая плоскость, проходящая через касательную кривой, является соприкасающейся.
определяет соприкасающуюся плоскость кривой (рис. 1).Дважды дифференцируемая кривая в каждой точке имеет соприкасающуюся плоскость.Она либо единственная, либо любая плоскость, проходящая через касательную кривой, является соприкасающейся. её соприкасающейся плоскости определяется из соотношения:
её соприкасающейся плоскости определяется из соотношения:

![{boldsymbol {r}}(lambda )={boldsymbol {r}}(t_{0})+lambda [{boldsymbol {r}}'(t_{0}),~{boldsymbol {r}}''(t_{0})].](https://wikimedia.org/api/rest_v1/media/math/render/svg/b484d034092a7ddfd4f6cea0efa4b3f9f0cac69f)
![{displaystyle [mathbf {r} ' [mathbf {r} ' mathbf {r} '']]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3f135b5614dea21d7483f78df4494d17407f5d11) .
.


 , когда P1, P2{displaystyle P_{1}, P_{2}}
, когда P1, P2{displaystyle P_{1}, P_{2}}


 имеет единичную длину и поэтому совпадает с ортом касательной.
имеет единичную длину и поэтому совпадает с ортом касательной. по длине совпадает с кривизной, а по направлению — с главной нормалью.
по длине совпадает с кривизной, а по направлению — с главной нормалью.![k_{1}={frac {left|[{mathbf {r}}'(t), {mathbf {r}}''(t)]right|}{left|{mathbf {r}}'(t)right|^{3}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7e3db8190f61a55ce8cf889d67c579c650eac107) ,
, — вектор-функция с координатами x(t), y(t), z(t){displaystyle x(t), y(t), z(t)}
— вектор-функция с координатами x(t), y(t), z(t){displaystyle x(t), y(t), z(t)}





 равна 1/R{displaystyle 1/R}
равна 1/R{displaystyle 1/R} .
. , определяется по формуле
, определяется по формуле .
. или −{displaystyle -}
или −{displaystyle -} берётся по соглашению, но сохраняется вдоль всей кривой.
берётся по соглашению, но сохраняется вдоль всей кривой.![k_{2}={frac {({mathbf {r}}',{mathbf {r}}'',{mathbf {r}}''')}{left|[{mathbf {r}}', {mathbf {r}}'']right|^{2}}},](https://wikimedia.org/api/rest_v1/media/math/render/svg/9505a0bf2172b4f91c94b1e69ccdda0b8b95c1ee)
 обозначает
обозначает 

 и k2 {displaystyle k_{2} }
и k2 {displaystyle k_{2} } — кривизна и кручение кривой в указанной точке.
— кривизна и кручение кривой в указанной точке. , соответственно для касательной, главной нормали и бинормали кривой, при движении вдоль кривой изменяются.При соответствующем выборе направления этих векторов из определения кривизны и кручения получаются формулы:
, соответственно для касательной, главной нормали и бинормали кривой, при движении вдоль кривой изменяются.При соответствующем выборе направления этих векторов из определения кривизны и кручения получаются формулы:


 (
(
 кривой. В связи с этим систему уравнения
кривой. В связи с этим систему уравнения





 ) и прямая ( a=0 {displaystyle a=0 }
) и прямая ( a=0 {displaystyle a=0 } ).
).