Двенадцатеричная система счисления — позиционная система счисления с основанием 12. Используются цифры 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B. Существует другая система обозначения, где для недостающих цифр используют не A и B, а T (от англ. ten, десять) или D (от лат. decem, фр. dix, десять) или X (римское десять), а также E (от англ. eleven, одиннадцать) или O (от фр. onze, одиннадцать).
Число 12 могло бы быть очень удобным основанием системы счисления, так как оно делится нацело на 2, 3, 4 и 6, в то время как число 10 — основание десятичной системы счисления — делится нацело лишь на 2 и 5.
Содержание
История
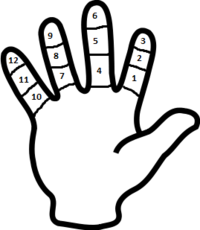
Двенадцатеричная система счисления возникла в древнем Шумере. Предполагается, что такая система возникала, исходя из количества фаланг четырёх пальцев руки (исключая большой) при подсчёте их большим пальцем той же руки.[1][2][3] Фаланги пальцев использовались как простейшие счёты (текущее состояние счёта засекалось большим пальцем), вместо загибания пальцев, принятого в европейской цивилизации. Некоторые народы Нигерии и Тибета используют двенадцатеричную систему счисления в настоящее время.
Также существует гипотеза, что до 12 считали сидя, загибая не только 10 пальцев рук, но и 2 ноги. Хотя, возможно, такое случалось, когда европейцам приходилось сталкиваться с восточным двенадцатеричным счётом.
Двенадцатые доли часто встречались и в европейских системах мер. У римлян стандартной дробью была унция (1/12). 1 английский пенни (пенс) = 1/12 шиллинга, 1 дюйм = 1/12 фута и т. д.
Переход на двенадцатеричную систему счисления предлагался неоднократно. В XVII веке её сторонником был знаменитый французский естествоиспытатель Бюффон. Вольтер в «Истории Карла XII» утверждает, что этот монарх готовил указ о переходе на двенадцатеричную систему.[4] Во времена Великой французской революции была учреждена «Революционная комиссия по весам и мерам», которая длительный период рассматривала подобный проект, однако усилиями Лагранжа и других противников реформы дело удалось свернуть. В 1944 году было организовано «Американское двенадцатеричное общество» (англ. The Dozenal Society of America (DSA)), а в 1959 — «Английское двенадцатеричное общество» (англ. The Dozenal Society of Great Britain (DSGB)), объединившие активных сторонников одноимённой системы счисления. Однако главным аргументом против этого всегда служили огромные затраты и неизбежная путаница при переходе. [источник не указан 2649 дней]
Двенадцатеричный счёт
Элементом двенадцатеричной системы в современности может служить счёт дюжинами. Первые три степени числа 12 имеют собственные названия:
К удобствам двенадцатеричного счисления можно отнести большее (по сравнению с десятичной системой) количество делителей основания 12 — 2, 3, 4, 6. На практике двенадцатеричная система (в смешанном виде) осталась в часах.
Упоминание в фантастике
Двенадцатеричная система счисления упоминается и в фантастической литературе:
- применяется эльфами в книгах Дж. Р. Р. Толкина.
- используется расой, заселившей Землю, после экспансии людей в галактику в романе Уолтера Миллера «Банк крови».
- используется людьми будущего в романе Герберта Уэллса «Когда спящий проснётся», новелле Гарри Гаррисона «История конца» и рассказе Джеймса Блиша «Маникюр».
- часто встречается в головоломках компьютерной игры Schizm 2 Chameleon
- применяется в Мире Стержня в циклах книг Макса Фрая
- в повести Джеральда Дэвида Нордли «Последняя инстанция» двенадцатеричной системой пользуется инопланетная раса ду’утианцев.
См. также
Примечания
- ↑ Nishikawa, Yoshiaki (2002), ヒマラヤの満月と十二進法 (The Full Moon in the Himalayas and the Duodecimal System), <http://www.kankyok.co.jp/nue/nue11/nue11_01.html>. Проверено 24 марта 2008.
- ↑ Ifrah, Georges (2000), The Universal History of Numbers: From prehistory to the invention of the computer., John Wiley and Sons, ISBN 0-471-39340-1
- ↑ Macey, Samuel L. The Dynamics of Progress: Time, Method, and Measure. — Atlanta, Georgia : University of Georgia Press, 1989. — P. 92. — ISBN 978-0-8203-3796-8.
- ↑ Депман И. Я. История арифметики. (1965), с. 31.
Ссылки
- Фомин С. В. Системы счисления. Серия «Популярные лекции по математике», выпуск 40. М.: Наука, 1987. 48 с.
- http://www.angelfire.com/whittenwords/measure/dozencount.htm
- http://www.earth360.com/math-naturesnumbers.html