У этого термина существуют и другие значения, см. Дельта (значения).
Де́льта-фу́нкция (или δ-функция, δ-функция Дирака, дираковская дельта, единичная импульсная функция) — обобщённая функция, которая позволяет записать точечное воздействие, а также пространственную плотность физических величин (масса, заряд, интенсивность источника тепла, сила и т. п.), сосредоточенной или приложенной в одной точке.
 Схематический график одномерной дельта-функции.
Схематический график одномерной дельта-функции.
Например, плотность единичной точечной массы m, находящейся в точке a для примера, одномерного евклидова пространства R1,{displaystyle mathbb {R} ^{1},} записывается с помощью δ{displaystyle delta }-функции в виде mδ(x−a).{displaystyle mdelta (x-a).} Дельта-функция также применима для описания распределений заряда, массы и т. п. на поверхностях или линиях.
δ{displaystyle delta }-Функция не является функцией в классическом смысле, а определяется как обобщённая функция: непрерывный линейный функционал на пространстве дифференцируемых функций. Можно ввести производную для δ-функции, которая тоже будет обобщённой функцией, и интеграл, определяемый как функция Хевисайда. Нетрудно указать последовательности обычных классических функций, слабо сходящиеся к δ{displaystyle delta }-функции.
Можно различать одномерную и многомерные дельта-функции, однако последние могут быть представлены в виде произведения одномерных функций в количестве, равном размерности пространства, на котором определена многомерная функция.
Введена английским физиком Полем Дираком.
Содержание
- 1 Определения
- 2 Свойства
- 3 δ-Функция как слабый предел
- 4 Интегральное представление
- 5 Производная дельта-функции
- 6 Преобразование Фурье
- 7 Представление многомерных дельта-функций в различных системах координат
- 8 Физическая интерпретация
- 9 См. также
- 10 Примечания
- 11 Литература
Определения
Существуют различные взгляды на понятие дельта-функции. Получающиеся при этом объекты, вообще говоря, различны, однако обладают рядом общих характерных свойств. Все указанные ниже конструкции естественно обобщаются на случаи пространств большей размерности (Rn, n>1){displaystyle (mathbb {R} ^{n}, n>1)}
.
Простое определение
Дельта-функцию (функция Дирака) одной вещественной переменной можно определить как функцию δ(x){displaystyle delta (x)}
, удовлетворяющую следующим условиям:
- δ(x)={+∞,x=0,0,x≠0;{displaystyle delta (x)=left{{begin{matrix}+infty ,&x=0,�,&xneq 0;end{matrix}}right.}
- ∫−∞+∞δ(x)dx=1.{displaystyle int limits _{-infty }^{+infty }delta (x),dx=1.}
То есть эта функция не равна нулю только в точке x=0{displaystyle x=0}
, где она обращается в бесконечность таким образом, чтобы её интеграл по любой окрестности x=0{displaystyle x=0} был равен 1. В этом смысле понятие дельта-функции аналогично физическим понятиям точечной массы или точечного заряда. Для понимания интеграла полезно представить себе некую фигуру на плоскости с единичной площадью, например, треугольник. Если уменьшать основание данного треугольника и увеличивать высоту так, чтобы площадь была неизменной, то в предельном случае мы получим треугольник с малым основанием и очень большой высотой. По предположению его площадь равна единице, что и показывает интеграл. Вместо треугольника можно без ограничения общности использовать любую фигуру. Аналогичные условия верны и для дельта-функций, определённых на Rn.{displaystyle mathbb {R} ^{n}.}
Эти равенства не принято считать определением дельта-функции, однако во многих учебниках по физике она определяется именно так, и этого достаточно для точного определения дельта-функции. Отметим, что из данного определения дельта-функции вытекает следующее равенство
- ∫−∞+∞δ(x−y)f(x)dx=f(y){displaystyle int limits _{-infty }^{+infty }delta (x-y)f(x),dx=f(y)}
(фильтрующее свойство) для любой функции f. Действительно, в силу свойства δ(x−y)=0{displaystyle delta (x-y)=0}
при x≠y{displaystyle xneq y} значение этого интеграла не изменится, если функцию f(x){displaystyle f(x)} заменить функцией f~(x){displaystyle {tilde {f}}(x)} , которая равна f(x){displaystyle f(x)} в точке x=y{displaystyle x=y} , а в остальных точках имеет произвольные значения. Например, берём f~(x)=f(y)=const{displaystyle {tilde {f}}(x)=f(y)=operatorname {const} } , затем выносим f(y){displaystyle f(y)} за знак интеграла и, используя второе условие в определении дельта-функции, получаем нужное равенство.
Производные от дельта-функции также почти всюду равны 0 и обращаются в ±∞{displaystyle pm infty }
при x=0{displaystyle x=0} .
Классическое определение
Дельта-функция определяется как линейный непрерывный функционал на некотором функциональном пространстве (пространстве основных функций). В зависимости от цели и желаемых свойств, это может быть пространство функций с компактным носителем, пространство функций, быстро убывающих на бесконечности, гладких функций на многообразии, аналитических функций и т. д. Для того, чтобы были определены производные дельта-функции с хорошими свойствами, во всех случаях основные функции берутся бесконечно дифференцируемыми, пространство основных функций также должно быть полным метрическим пространством. Общий подход к обобщённым функциям см. в соответствующей статье. Такие обобщённые функции также называют распределениями.
Мы рассмотрим самый простой вариант. В качестве пространства основных функций рассмотрим пространство E{displaystyle {mathcal {E}}}
всех бесконечно дифференцируемых функций на отрезке. Последовательность φn∈E{displaystyle varphi _{n}in {mathcal {E}}} сходится к φ∈E{displaystyle varphi in {mathcal {E}}} , если на любом компакте K∈R{displaystyle Kin mathbb {R} } функции φn{displaystyle varphi _{n}} сходятся к φ{displaystyle varphi } равномерно вместе со всеми своими производными:
- limn→∞φn=φ⟺supjsupx∈K|φn(j)(x)−φ(j)(x)|→n→∞0.{displaystyle lim _{nto infty }varphi _{n}=varphi iff sup _{j}sup _{xin K}left|varphi _{n}^{(j)}(x)-varphi ^{(j)}(x)right|{xrightarrow {nto infty }},0.}
Это локально выпуклое метризуемое пространство. Дельта-функцию определим как функционал δ∈E′{displaystyle delta in {mathcal {E}}^{prime }}
, такой что
- ∀φ∈E:⟨δ;φ⟩=φ(0).{displaystyle forall varphi in {mathcal {E}}:;langle delta ;;varphi rangle =varphi (0).}
Непрерывность означает, что если φn→φ{displaystyle varphi _{n}to varphi }
, то ⟨δ;φn⟩→⟨δ;φ⟩{displaystyle langle delta ;;varphi _{n}rangle to langle delta ;;varphi rangle } . Здесь ⟨δ;φ⟩{displaystyle langle delta ;;varphi rangle } — значение функционала на функции φ{displaystyle varphi } . Для удобства это записывают как
- ⟨δ;φ⟩=∫−∞∞δ(x)φ(x)dx.{displaystyle langle delta ;;varphi rangle =int _{-infty }^{infty }delta (x)varphi (x),dx.}
Заметим, что при таком подходе интегральная запись есть не больше, чем формальное обозначение, облегчающее восприятие формул.
Дельта-функция по Коломбо
Используемому для работы с дельта-функцией интегральному выражению можно придать смысл, близкий к интуитивному, в рамках теории алгебры обобщённых функций Коломбо (англ. Colombeau algebra) [1].
Пусть D{displaystyle {mathcal {D}}}
— множество бесконечно дифференцируемых функций f:R→R{displaystyle fcolon mathbb {R} to mathbb {R} } с компактным носителем, то есть не равных нулю лишь на ограниченном множестве. Рассмотрим множество функций
- A={φ∈D|∫Rφ(x)dx=1,∫Rxφ(x)dx=0}.{displaystyle {mathcal {A}}=left{varphi in {mathcal {D}},{bigg |}int _{mathbb {R} }varphi (x),dx=1,;int _{mathbb {R} }xvarphi (x),dx=0right}.}
Обобщённая функция — это класс эквивалентности функций R:A×R→R,{displaystyle Rcolon {mathcal {A}}times mathbb {R} to mathbb {R} ,}
R:(φ,x)↦R(φ,x),{displaystyle Rcolon (varphi ,;x)mapsto R(varphi ,;x),} бесконечно дифференцируемых по x при каждом φ∈A{displaystyle varphi in {mathcal {A}}} и удовлетворяющих некоторому условию умеренности (полагая φε(x)=ε−1φ(xε−1),{displaystyle varphi _{varepsilon }(x)=varepsilon ^{-1}varphi (xvarepsilon ^{-1}),} R(φε,x){displaystyle R(varphi _{varepsilon },;x)} и все её производные по x достаточно медленно растут при ε→0{displaystyle varepsilon to 0} ). Две функции полагаются эквивалентными, если R1−R2∈N{displaystyle R_{1}-R_{2}in {mathcal {N}}} , где N{displaystyle {mathcal {N}}} — ещё один класс функций с ограничениями на рост R(φε,x){displaystyle R(varphi _{varepsilon },;x)} при ε→0.{displaystyle varepsilon to 0.}
Дельта-функция определяется как δ(φ,x)=φ(−x).{displaystyle delta (varphi ,;x)=varphi (-x).}
Преимущество подхода Коломбо в том, что его обобщённые функции образуют коммутативную ассоциативную алгебру, при этом на множество обобщённых функций естественно продолжаются понятия интегрирования, дифференцирования, пределов, даже значения в точке. В этом смысле на дельта-функцию действительно можно смотреть как на функцию, равную 0 везде, кроме точки 0, и равную бесконечности в нуле, так как теория Коломбо включает в себя теорию бесконечно больших и бесконечно малых чисел, аналогично нестандартному анализу.
Подход Егорова
Аналогичная теория обобщённых функций была изложена в работе Ю. В. Егорова[2]. Хотя она не эквивалентна теории Коломбо, конструкция значительно проще и обладает большинством желаемых свойств.
Обобщённая функция — это класс эквивалентности последовательностей f=(f1,f2,…),fi∈C∞(R).{displaystyle f=(f_{1},;f_{2},;ldots ),;f_{i}in C^{infty }(mathbb {R} ).}
Последовательности f{displaystyle f} и f~{displaystyle {tilde {f}}} считаются эквивалентными, если для любого компакта Ω⋐R{displaystyle Omega Subset mathbb {R} } функции последовательностей совпадают на Ω{displaystyle Omega } начиная с некоторого номера:
- f∼f~⟺∀Ω⋐R ∃N ∀k>N:fk|Ω=f~k|Ω.{displaystyle fsim {tilde {f}}iff forall Omega Subset mathbb {R} exists N forall k>Ncolon f_{k}|_{Omega }={tilde {f}}_{k}|_{Omega }.}
Всевозможные операции над последовательностями (умножение, сложение, интегрирование, дифференцирование, композиция, …) определяются покомпонентно. Например, интеграл по множеству I определяется как класс эквивалентности последовательности
- ∫If(x)dx=[(a1,a2,…)],ai=∫Ifi(x)dx.{displaystyle int _{I}f(x),dx=[(a_{1},;a_{2},;ldots )],;a_{i}=int _{I}f_{i}(x),dx.}
Две обобщённые функции слабо равны, если для любой бесконечно гладкой функции φ{displaystyle varphi }
- limk→∞∫I(fk(x)−f~k(x))φ(x)dx=0.{displaystyle lim _{kto infty }int _{I}(f_{k}(x)-{tilde {f}}_{k}(x))varphi (x),dx=0.}
При этом дельта-функция определяется любой дельта-образной последовательностью (см. ниже), все такие обобщённые функции слабо равны.
Свойства
- Интеграл от дельта-функции по любому интервалу, содержащему в себе ноль, то есть интервалу вида (−a1,a2),{displaystyle (-a_{1},;a_{2}),} где a1{displaystyle a_{1}} и a2{displaystyle a_{2}} — произвольные действительные положительные числа, равен 1.
- xδ′(x)=−δ(x).{displaystyle xdelta ^{prime }(x)=-delta (x).}
- δ(f(x))=∑kδ(x−xk)|f′(xk)|{displaystyle delta (f(x))=sum _{k}{frac {delta (x-x_{k})}{|f'(x_{k})|}}} , где xk{displaystyle x_{k}} — простые нули функции f(x){displaystyle f(x)} .
- Первообразной одномерной дельта-функции является функция Хевисайда:
- θ(x)={0,x<0,12,x=0,1,x>0.{displaystyle theta (x)=left{{begin{array}{*{35}{l}}0,&x<0,{dfrac {1}{2}},&x=0,1,&x>0.end{array}}right.}
- Фильтрующее свойство дельта-функции:
∫−∞+∞f(x)δ(x−x0)dx=f(x0).{displaystyle int limits _{-infty }^{+infty }f(x)delta (x-x_{0}),dx=f(x_{0}).}
δ-Функция как слабый предел
Пусть ∫−∞+∞f(x)dx=1.{displaystyle int limits _{-infty }^{+infty }f(x),dx=1.}
Тогда последовательность
- fn(x)=nf(nx){displaystyle f_{n}(x)=nf(nx)}
слабо сходится к δ{displaystyle delta }
-функции. График функции sinxx.{displaystyle {frac {sin x}{x}}.}
График функции sinxx.{displaystyle {frac {sin x}{x}}.}
Часто в качестве f(x){displaystyle ~f(x)}
выбирают
- f(x)=sinxπx,{displaystyle f(x)={frac {sin x}{pi x}},}
дающую последовательность
- fn(x)=nsin(nx)nπx.{displaystyle f_{n}(x)=n{frac {sin(nx)}{npi x}}.}
Если нужно, чтобы члены последовательности были всюду положительными функциями, можно исходить из Гауссова колокола:
- f(x)=1πe−x2,{displaystyle f(x)={frac {1}{sqrt {pi }}}e^{-x^{2}},}
- fn(x)=nπe−(nx)2.{displaystyle f_{n}(x)={frac {n}{sqrt {pi }}}e^{-(nx)^{2}}.}
Интегральное представление
Во многих приложениях оказывается удобным интегральное представление дельта-функции:
- δ(t)=12π∫−∞+∞eiωtdω.{displaystyle delta (t)={frac {1}{2pi }}int limits _{-infty }^{+infty }e^{iomega t},domega .}
Доказательство
Рассмотрим интеграл
- I(t)=12π∫−∞∞eiωtdω,{displaystyle I(t)={frac {1}{2pi }}int limits _{-infty }^{infty }e^{iomega t},domega ,} (1)
который можно интерпретировать как предел
- I(t)=limN→∞IN(t),{displaystyle I(t)=lim _{Nto infty }I_{N}(t),,}
где
- IN(t)=12π∫−NNeiωtdω=1πNsintNtN.{displaystyle I_{N}(t)={frac {1}{2pi }}int limits _{-N}^{N}e^{iomega t},domega ={frac {1}{pi }}N{frac {sin {tN}}{tN}}.} (2)
Известно, что
- ∫−∞∞sinttdt=π.{displaystyle int limits _{-infty }^{infty }{frac {sin t}{t}},dt=pi .} (3)
В силу (3) для любого N{displaystyle N}
справедливо равенство:
- ∫−∞∞IN(t)dt=1π∫−∞∞sintNtNd(tN)=1.{displaystyle int limits _{-infty }^{infty }I_{N}(t),dt={frac {1}{pi }}int limits _{-infty }^{infty }{frac {sin {tN}}{tN}},d(tN)=1.} (4)
Можно показать (см. выше), что при неограниченном росте N для функции (2) оказываются верными все свойства дельта-функции и она в некотором смысле стремится к δ(t).{displaystyle ~delta (t).}
Производная дельта-функции
По определению производной дельта-функции δ(x){displaystyle delta (x)}
:
- ∫−∞+∞f(x)δ′(x−a)dx=−f′(a){displaystyle int limits _{-infty }^{+infty }f(x)delta ^{prime }(x-a),dx=-f^{prime }(a)}
(распространение интегрирования по частям на случай подынтегральных выражений, содержащих дельта-функцию).
Аналогично для n-й производной дельта-функции:
- ∫−∞+∞f(x)δ[n](x−a)dx=−∫−∞+∞∂f∂xδ[n−1](x−a)dx.{displaystyle int limits _{-infty }^{+infty }f(x)delta ^{[n]}(x-a),dx=-int limits _{-infty }^{+infty }{frac {partial f}{partial x}}delta ^{[n-1]}(x-a),dx.}
А проинтегрировав так по частям n раз, получим в конце концов:
- ∫−∞+∞f(x)δ[n](x−a)dx=(−1)n∂nf(x)∂xn|x=a.{displaystyle int limits _{-infty }^{+infty }f(x)delta ^{[n]}(x-a),dx=left.(-1)^{n}{frac {partial ^{n}f(x)}{partial x^{n}}}right|_{x=a}.}
Для производной дельта-функции имеет место тождество:
- f(x)δ′(x)=f(0)δ′(x)−f′(0)δ(x),{displaystyle f(x)delta ^{prime }(x)=f(0)delta ^{prime }(x)-f^{prime }(0)delta (x),}
которое можно получить дифференцируя произведение f(x)δ(x){displaystyle f(x)delta (x)}
.
Преобразование Фурье
- В этом параграфе мы будем применять нормировку, соответствующую соглашению о единичном коэффициенте в обратном преобразовании, то есть имея в виду f(t)=12π∫−∞+∞F(ω)eiωtdω.{displaystyle f(t)={frac {1}{sqrt {2pi }}}int limits _{-infty }^{+infty }F(omega )e^{iomega t},domega .}
- Формулы этого параграфа имеют соответствующие аналоги для многомерного преобразования Фурье.
К дельта-функции можно применить преобразование Фурье:
- F{δ(t−t0)}(ω)=12π∫−∞+∞δ(t−t0)⋅e−iωtdt=12πe−iω⋅t0.{displaystyle Fleft{delta (t-t_{0})right}(omega )={frac {1}{sqrt {2pi }}}int limits _{-infty }^{+infty }delta (t-t_{0})cdot e^{-iomega t},dt={frac {1}{sqrt {2pi }}}e^{-iomega cdot t_{0}}.}
Таким образом, спектр (Фурье-образ) дельта-функции, центрированной в точке t0{displaystyle t_{0}}
, является „волной“ в пространстве частот, обладающей „периодом“ 2πt0{displaystyle {frac {2pi }{t_{0}}}} . В частности, спектр (Фурье-образ) дельта-функции, центрированной в нуле, является константой (нестрого говоря — „волной“ с бесконечно большим „периодом“):
- F{δ(t)}(ω)=12πe−iω⋅0=12π.{displaystyle Fleft{delta (t)right}(omega )={frac {1}{sqrt {2pi }}}e^{-iomega cdot 0}={frac {1}{sqrt {2pi }}}.}
Представление многомерных дельта-функций в различных системах координат
В n-мерном пространстве в декартовых координатах (ортонормированном базисе):
- ∫δn(x1,x2,…,xn)dnx=1;{displaystyle int delta ^{n}(x_{1},;x_{2},;ldots ,;x_{n}),d^{n}x=1;}
- δn(x1,x2,…,xn)=δ(x1)δ(x2)…δ(xn).{displaystyle delta ^{n}(x_{1},;x_{2},;ldots ,;x_{n})=delta (x_{1})delta (x_{2})ldots delta (x_{n}).}
В двумерном пространстве:
- ∬−∞+∞δ2(x,y)dxdy=1;{displaystyle iint limits _{-infty }^{+infty }delta ^{2}(x,;y),dx,dy=1;}
- δ2(ax,by)=1|ab|δ2(x,y);{displaystyle delta ^{2}(ax,;by)={frac {1}{left|abright|}}delta ^{2}(x,;y);}
- δ2(x,y)=δ(x)δ(y).{displaystyle delta ^{2}(x,;y)=delta (x)delta (y).}
В полярных координатах:
- δ2(r,φ)=δ(r)2π|r|{displaystyle delta ^{2}(r,;varphi )={frac {delta (r)}{2pi left|rright|}}} — несмещённая относительно начала координат (с особенностью при r=0),
- δ(r−r0)δ(φ−φ0)|r|{displaystyle {frac {delta (r-r_{0})delta (varphi -varphi _{0})}{|r|}}} — с особенностью в точке общего положения (r0,φ0);{displaystyle (r_{0},;varphi _{0});} при r=0 доопределяется нулём.
В трёхмерном пространстве:
- ∭−∞+∞δ3(x,y,z)dxdydz=1;{displaystyle iiint limits _{-infty }^{+infty }delta ^{3}(x,;y,;z),dx,dy,dz=1;}
- δ3(x,y,z)=δ(x)δ(y)δ(z).{displaystyle delta ^{3}(x,;y,;z)=delta (x)delta (y)delta (z).}
В цилиндрической системе координат:
- δ3(r,θ,z)=δ(r)δ(z)2πr{displaystyle delta ^{3}(r,;theta ,;z)={frac {delta (r)delta (z)}{2pi r}}} — несмещённая относительно начала координат (с особенностью при r=0,z=0{displaystyle r=0,;z=0} ),
- δ(r−r0)δ(φ−φ0)δ(z−z0)|r|{displaystyle {frac {delta (r-r_{0})delta (varphi -varphi _{0})delta (z-z_{0})}{|r|}}} — с особенностью в точке общего положения (r0,φ0,z0);{displaystyle (r_{0},;varphi _{0},;z_{0});} при r=0 доопределяется нулём.
В сферической системе координат:
- δ3(r,θ,φ)=δ(r)4πr2{displaystyle delta ^{3}(r,;theta ,;varphi )={frac {delta (r)}{4pi r^{2}}}} — несмещённая относительно начала координат (с особенностью при r=0).
- В формулах с особенностью в начале координат нередко используют вдвое большие коэффициенты (1/π для цилиндрической и полярной, 1/2π для сферической). Это связано с тем, что предполагается вдвое меньший результат интегрирования в случае, если особая точка находится точно на границе интервала интегрирования.
Физическая интерпретация
Вблизи заряженной точки поле бесконечно, ряды Тейлора для поля не сходятся, поэтому вводят специальные функции. Одной из таких функций является дельта-функция. Вопрос о поле точечной заряженной частицы сравнительно сложен, поэтому рассмотрим сначала более простой пример.
Мгновенное ускорение
Пусть частица, способная перемещаться вдоль прямой, при ударе пренебрежимо малой длительности скачком приобретает какую-то скорость. Зададимся вопросом: как рассчитать ускорение, приобретённое телом? Построим график зависимости изменения скорости от времени. График будет иметь следующий вид:
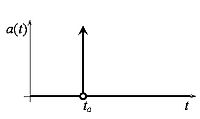
Данный график почти всюду является графиком функции Хевисайда. Производная функции Хевисайда является единичной дельта-функцией, график которой условно можно изобразить как
Данный график отображает бесконечное ускорение при мгновенном наборе скорости. В общем случае ускорение при ударе можно записать как
- a(t)=νδ(t−ta). {displaystyle a(t)=nu delta (t-t_{a}). }
Масса материальной точки
Если нужно найти суммарную массу (или заряд) некоторого непрерывного распределения плотности (или плотности заряда) m=∫ρcontin,{displaystyle m=int rho _{mathrm {contin} },}
содержащего, кроме того, точечные массы (заряды), то удобно вместо формулы, учитывающей отдельно дискретные массы и непрерывную конечную плотность:
- m=∫ρcontin(x)dV+∑iqi{displaystyle m=int rho _{mathrm {contin} }(mathbf {x} ),dV+sum _{i}q_{i}}
записывать просто:
- m=∫ρ(x)dV,{displaystyle m=int rho (mathbf {x} ),dV,}
имея в виду, что ρ(x){displaystyle rho (mathbf {x} )}
имеет как непрерывную, так и дельтообразные (по одной для каждой точечной массы) составляющие:
- ρ(x)=ρcontin(x)+∑iqiδ(x−xi).{displaystyle rho (mathbf {x} )=rho _{mathrm {contin} }(mathbf {x} )+sum _{i}q_{i}delta (mathbf {x} -mathbf {x} _{i}).}
Другие примеры
- Дельта-функция применяется в математической физике при решении задач, в которые входят сосредоточенные величины. В квазиклассическом пределе (ℏ→0{displaystyle hbar rightarrow 0} ) квантовой механики волновые функции локализуются в волновые пакеты с дельтообразными (то есть имеющими в пределе форму дельта-функции) огибающими, и области их локализации движутся по классическим траекториям согласно уравнениям Ньютона.
- Преобразование Фурье единицы является дельта-функцией. Это позволяет более удобно и математически строго формулировать различные задачи, связанные с преобразованием Фурье, которые очень многочисленны: волновая оптика, акустика, теория колебаний. В квантовой механике преобразования Фурье волновых функций играют первостепенную принципиальную и техническую роль, именно для неё Дирак впервые ввёл дельта-функцию.
- Дельта-функции играют роль собственных функций оператора с непрерывным спектром в представлениях, где этот оператор диагонален. Таким образом, они играют роль базиса в диагональном представлении оператора.
- Важным применением дельта-функции является их участие в аппарате функций Грина линейных операторов. Для линейного оператора L, действующего на обобщённые функции над многообразием M, уравнение, определяющее функцию Грина g с источником в точке x0,{displaystyle x_{0},} имеет вид
- Lg(x,x0)=δ(x−x0).{displaystyle L,g(x,;x_{0})=delta (x-x_{0}).}
- Особенно часто встречается применение этого аппарата к оператору Лапласа (электростатика, теплопроводность, диффузия, механическая теория упругости) и подобным ему операторам, таким как Оператор Д’Аламбера (акустика, электродинамика, квантовая теория поля, где функция Грина часто носит специальное название пропагатора).
- Для лапласиана в R3{displaystyle mathbb {R} ^{3}} функцией Грина является функция 1/r, так что
-
- Δ(1r)=−4πδ(r),{displaystyle Delta left({frac {1}{r}}right)=-4pi delta (mathbf {r} ),}
- где r — расстояние до начала координат. Этот факт используется для доказательства того, что выражение для скалярного потенциала
- Φ(x)=−∫ϱ(x′)|x−x′|d3x′{displaystyle Phi (mathbf {x} )=-int {frac {varrho (mathbf {x} ^{prime })}{left|mathbf {x} -mathbf {x} ^{prime }right|}},d^{3}x^{prime }}
- удовлетворяет уравнению Пуассона:
- ΔΦ=−4πϱ.{displaystyle Delta Phi =-4pi varrho .}
См. также
Примечания
- ↑ Colombeau J. F. Elementary Introduction to New Generalized Functions. — Amsterdam: Elsevier Science Publishers B. V., 1985. — 281 с. — ISBN 978-0-444-87756-7.
- ↑ Егоров Ю. В. К теории обобщённых функций // УМН. — 1990. — Т. 45, вып. 5 (275). — С. 3—40.
Литература
- Дирак П. А. М. Основы квантовой механики / Пер. с англ. — М., 1932 (есть много переизданий).
- Кудрявцев Л. Д. Краткий курс математического анализа. — Том 2. — ISBN 5-9221-0185-4.
- Weisstein, Eric W. Delta Function (англ.) на сайте Wolfram MathWorld.
- Хермандер Л. Анализ линейных дифференциальных уравнений. — Том 1.
- Хермандер Л. Линейные дифференциальные операторы в частных производных.
- Гельфанд И. М., Шилов Г. Е. Обобщённые функции и действия над ними.
- Краснопевцев Е. А. Математические методы физики. Избранные вопросы.
| Для улучшения этой статьи по математике желательно:
После исправления проблемы исключите её из списка. Удалите шаблон, если устранены все недостатки. |
 записывается с помощью δ{displaystyle delta }
записывается с помощью δ{displaystyle delta } -функции в виде mδ(x−a).{displaystyle mdelta (x-a).}
-функции в виде mδ(x−a).{displaystyle mdelta (x-a).} Дельта-функция также применима для описания распределений заряда, массы и т. п. на поверхностях или линиях.
Дельта-функция также применима для описания распределений заряда, массы и т. п. на поверхностях или линиях. .
. , удовлетворяющую следующим условиям:
, удовлетворяющую следующим условиям:

 , где она обращается в бесконечность таким образом, чтобы её интеграл по любой окрестности x=0{displaystyle x=0}
, где она обращается в бесконечность таким образом, чтобы её интеграл по любой окрестности x=0{displaystyle x=0}

 при x≠y{displaystyle xneq y}
при x≠y{displaystyle xneq y} значение этого интеграла не изменится, если функцию f(x){displaystyle f(x)}
значение этого интеграла не изменится, если функцию f(x){displaystyle f(x)} заменить функцией f~(x){displaystyle {tilde {f}}(x)}
заменить функцией f~(x){displaystyle {tilde {f}}(x)} , которая равна f(x){displaystyle f(x)}
, которая равна f(x){displaystyle f(x)} , а в остальных точках имеет произвольные значения. Например, берём f~(x)=f(y)=const{displaystyle {tilde {f}}(x)=f(y)=operatorname {const} }
, а в остальных точках имеет произвольные значения. Например, берём f~(x)=f(y)=const{displaystyle {tilde {f}}(x)=f(y)=operatorname {const} } , затем выносим f(y){displaystyle f(y)}
, затем выносим f(y){displaystyle f(y)} за знак интеграла и, используя второе условие в определении дельта-функции, получаем нужное равенство.
за знак интеграла и, используя второе условие в определении дельта-функции, получаем нужное равенство. при x=0{displaystyle x=0}
при x=0{displaystyle x=0} всех бесконечно дифференцируемых функций на отрезке. Последовательность φn∈E{displaystyle varphi _{n}in {mathcal {E}}}
всех бесконечно дифференцируемых функций на отрезке. Последовательность φn∈E{displaystyle varphi _{n}in {mathcal {E}}} сходится к φ∈E{displaystyle varphi in {mathcal {E}}}
сходится к φ∈E{displaystyle varphi in {mathcal {E}}} , если на любом компакте K∈R{displaystyle Kin mathbb {R} }
, если на любом компакте K∈R{displaystyle Kin mathbb {R} } функции φn{displaystyle varphi _{n}}
функции φn{displaystyle varphi _{n}} сходятся к φ{displaystyle varphi }
сходятся к φ{displaystyle varphi } равномерно вместе со всеми своими производными:
равномерно вместе со всеми своими производными:
 , такой что
, такой что
 , то ⟨δ;φn⟩→⟨δ;φ⟩{displaystyle langle delta ;;varphi _{n}rangle to langle delta ;;varphi rangle }
, то ⟨δ;φn⟩→⟨δ;φ⟩{displaystyle langle delta ;;varphi _{n}rangle to langle delta ;;varphi rangle } . Здесь ⟨δ;φ⟩{displaystyle langle delta ;;varphi rangle }
. Здесь ⟨δ;φ⟩{displaystyle langle delta ;;varphi rangle } — значение функционала на функции φ{displaystyle varphi }
— значение функционала на функции φ{displaystyle varphi }
 — множество бесконечно дифференцируемых функций f:R→R{displaystyle fcolon mathbb {R} to mathbb {R} }
— множество бесконечно дифференцируемых функций f:R→R{displaystyle fcolon mathbb {R} to mathbb {R} } с компактным носителем, то есть не равных нулю лишь на ограниченном множестве. Рассмотрим множество функций
с компактным носителем, то есть не равных нулю лишь на ограниченном множестве. Рассмотрим множество функций
 R:(φ,x)↦R(φ,x),{displaystyle Rcolon (varphi ,;x)mapsto R(varphi ,;x),}
R:(φ,x)↦R(φ,x),{displaystyle Rcolon (varphi ,;x)mapsto R(varphi ,;x),} бесконечно дифференцируемых по x при каждом φ∈A{displaystyle varphi in {mathcal {A}}}
бесконечно дифференцируемых по x при каждом φ∈A{displaystyle varphi in {mathcal {A}}} и удовлетворяющих некоторому условию умеренности (полагая φε(x)=ε−1φ(xε−1),{displaystyle varphi _{varepsilon }(x)=varepsilon ^{-1}varphi (xvarepsilon ^{-1}),}
и удовлетворяющих некоторому условию умеренности (полагая φε(x)=ε−1φ(xε−1),{displaystyle varphi _{varepsilon }(x)=varepsilon ^{-1}varphi (xvarepsilon ^{-1}),} R(φε,x){displaystyle R(varphi _{varepsilon },;x)}
R(φε,x){displaystyle R(varphi _{varepsilon },;x)} и все её производные по x достаточно медленно растут при ε→0{displaystyle varepsilon to 0}
и все её производные по x достаточно медленно растут при ε→0{displaystyle varepsilon to 0} ). Две функции полагаются эквивалентными, если R1−R2∈N{displaystyle R_{1}-R_{2}in {mathcal {N}}}
). Две функции полагаются эквивалентными, если R1−R2∈N{displaystyle R_{1}-R_{2}in {mathcal {N}}} , где N{displaystyle {mathcal {N}}}
, где N{displaystyle {mathcal {N}}} — ещё один класс функций с ограничениями на рост R(φε,x){displaystyle R(varphi _{varepsilon },;x)}
— ещё один класс функций с ограничениями на рост R(φε,x){displaystyle R(varphi _{varepsilon },;x)}
 Преимущество подхода Коломбо в том, что его обобщённые функции образуют
Преимущество подхода Коломбо в том, что его обобщённые функции образуют  Последовательности f{displaystyle f}
Последовательности f{displaystyle f} и f~{displaystyle {tilde {f}}}
и f~{displaystyle {tilde {f}}} считаются эквивалентными, если для любого компакта Ω⋐R{displaystyle Omega Subset mathbb {R} }
считаются эквивалентными, если для любого компакта Ω⋐R{displaystyle Omega Subset mathbb {R} } функции последовательностей совпадают на Ω{displaystyle Omega }
функции последовательностей совпадают на Ω{displaystyle Omega } начиная с некоторого номера:
начиная с некоторого номера:
![int_I f(x),dx=[(a_1,;a_2,;ldots)],;a_i=int_I f_i(x),dx.](https://wikimedia.org/api/rest_v1/media/math/render/svg/5436648292c10f1b49cc12960a1c54984da3becc)

 где a1{displaystyle a_{1}}
где a1{displaystyle a_{1}} и a2{displaystyle a_{2}}
и a2{displaystyle a_{2}} — произвольные действительные положительные числа, равен 1.
— произвольные действительные положительные числа, равен 1.
 , где xk{displaystyle x_{k}}
, где xk{displaystyle x_{k}} — простые нули функции f(x){displaystyle f(x)}
— простые нули функции f(x){displaystyle f(x)}





 выбирают
выбирают




 (1)
(1)
 (2)
(2) (3)
(3) справедливо равенство:
справедливо равенство: (4)
(4)

![intlimits_{-infty}^{+infty}f(x)delta^{[n]}(x-a),dx=-intlimits_{-infty}^{+infty}frac{partial f}{partial x}delta^{[n-1]}(x-a),dx.](https://wikimedia.org/api/rest_v1/media/math/render/svg/39dcd65ddc90e7b98739f7ceaae2748aa7d0d7fe)
![intlimits_{-infty}^{+infty}f(x)delta^{[n]}(x-a),dx=left.(-1)^nfrac{partial^n f(x)}{partial x^n}right|_{x=a}.](https://wikimedia.org/api/rest_v1/media/math/render/svg/c2d832072d2bf85d5c3682d438d2901ea3a41724)

 .
.

 , является „волной“ в пространстве частот, обладающей „периодом“ 2πt0{displaystyle {frac {2pi }{t_{0}}}}
, является „волной“ в пространстве частот, обладающей „периодом“ 2πt0{displaystyle {frac {2pi }{t_{0}}}} . В частности, спектр (Фурье-образ) дельта-функции, центрированной в нуле, является константой (нестрого говоря — „волной“ с бесконечно большим „периодом“):
. В частности, спектр (Фурье-образ) дельта-функции, центрированной в нуле, является константой (нестрого говоря — „волной“ с бесконечно большим „периодом“):





 — несмещённая относительно начала координат (с особенностью при r=0),
— несмещённая относительно начала координат (с особенностью при r=0), — с особенностью в точке общего положения (r0,φ0);{displaystyle (r_{0},;varphi _{0});}
— с особенностью в точке общего положения (r0,φ0);{displaystyle (r_{0},;varphi _{0});} при r=0 доопределяется нулём.
при r=0 доопределяется нулём.

 — несмещённая относительно начала координат (с особенностью при r=0,z=0{displaystyle r=0,;z=0}
— несмещённая относительно начала координат (с особенностью при r=0,z=0{displaystyle r=0,;z=0} ),
), — с особенностью в точке общего положения (r0,φ0,z0);{displaystyle (r_{0},;varphi _{0},;z_{0});}
— с особенностью в точке общего положения (r0,φ0,z0);{displaystyle (r_{0},;varphi _{0},;z_{0});} при r=0 доопределяется нулём.
при r=0 доопределяется нулём. — несмещённая относительно начала координат (с особенностью при r=0).
— несмещённая относительно начала координат (с особенностью при r=0).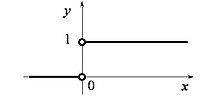

 содержащего, кроме того, точечные массы (заряды), то удобно вместо формулы, учитывающей отдельно дискретные массы и непрерывную конечную плотность:
содержащего, кроме того, точечные массы (заряды), то удобно вместо формулы, учитывающей отдельно дискретные массы и непрерывную конечную плотность:

 имеет как непрерывную, так и дельтообразные (по одной для каждой точечной массы) составляющие:
имеет как непрерывную, так и дельтообразные (по одной для каждой точечной массы) составляющие:
 )
)  имеет вид
имеет вид




