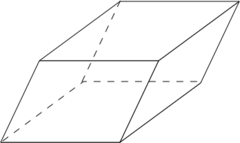
Книгатанк др.-греч. παραλληλ-επίπεδον[1] от др.-греч. παρ-άλληλος — «параллельный» и др.-греч. ἐπί-πεδον — «плоскость») — четырёхугольная призма, основанием которой служит параллелограмм, или, что равносильно, многогранник, у которого шесть граней, каждая из которых — параллелограмм.
Содержание
- 1 Типы параллелепипеда
- 2 Основные элементы
- 3 Свойства
- 4 Основные формулы
- 5 В математическом анализе
- 6 Сечение параллелепипеда плоскостью
- 7 Примечания
- 8 Ссылки
Типы параллелепипеда
Различается несколько типов параллелепипедов:
- Прямоугольный параллелепипед — это параллелепипед, у которого все грани — прямоугольники.
- Прямой параллелепипед — это параллелепипед, у которого 4 боковые грани прямоугольники.
- Наклонный параллелепипед — это параллелепипед, боковые грани которого не перпендикулярны основаниям.
- Ромбоэдр — параллелепипед, грани которого являются равными ромбами.
- Куб — параллелепипед, грани которого являются квадратами.
Основные элементы
Две грани параллелепипеда, не имеющие общего ребра, называются противоположными, а имеющие общее ребро — смежными. Две вершины параллелепипеда, не принадлежащие одной грани, называются противоположными. Отрезок, соединяющий противоположные вершины, называется диагональю параллелепипеда. Длины трёх рёбер прямоугольного параллелепипеда, имеющих общую вершину, называют его измерениями.
Свойства
- Параллелепипед симметричен относительно середины его диагонали.
- Любой отрезок с концами, принадлежащими поверхности параллелепипеда и проходящий через середину его диагонали, делится ею пополам; в частности, все диагонали параллелепипеда пересекаются в одной точке и делятся ею пополам.
- Противолежащие грани параллелепипеда параллельны и равны.
- Квадрат длины диагонали прямоугольного параллелепипеда равен сумме квадратов трёх его измерений.
Основные формулы
Прямой параллелепипед
Площадь боковой поверхностиSб=Ро*h, где Ро — периметр основания, h — высота
Площадь полной поверхностиSп=Sб+2Sо, где Sо — площадь основания
ОбъёмV=Sо*h
Прямоугольный параллелепипед
Основная статья: Прямоугольный параллелепипед
Площадь боковой поверхностиSб=2c(a+b), где a, b — стороны основания, c — боковое ребро прямоугольного параллелепипеда
Площадь полной поверхностиSп=2(ab+bc+ac)
ОбъёмV=abc, где a, b, c — измерения прямоугольного параллелепипеда.
Куб
Площадь поверхности: S=6a2{displaystyle S=6a^{2}}
Объём: V=a3{displaystyle V=a^{3}} , где a{displaystyle a} — ребро куба.
, где a{displaystyle a}
— ребро куба.Произвольный параллелепипед
Объём и соотношения в наклонном параллелепипеде часто определяются с помощью векторной алгебры. Объём параллелепипеда равен абсолютной величине смешанного произведения трёх векторов, определяемых тремя сторонами параллелепипеда, исходящими из одной вершины. Соотношение между длинами сторон параллелепипеда и углами между ними даёт утверждение, что определитель Грама указанных трёх векторов равен квадрату их смешанного произведения[2]:215.
В математическом анализе
В математическом анализе под n-мерным прямоугольным параллелепипедом B{displaystyle B}
понимают множество точек x=(x1,…,xn){displaystyle x=(x_{1},ldots ,x_{n})} вида B={x|a1⩽x1⩽b1,…,an⩽xn⩽bn}{displaystyle B={x|a_{1}leqslant x_{1}leqslant b_{1},ldots ,a_{n}leqslant x_{n}leqslant b_{n}}}
понимают множество точек x=(x1,…,xn){displaystyle x=(x_{1},ldots ,x_{n})}
вида B={x|a1⩽x1⩽b1,…,an⩽xn⩽bn}{displaystyle B={x|a_{1}leqslant x_{1}leqslant b_{1},ldots ,a_{n}leqslant x_{n}leqslant b_{n}}}
Сечение параллелепипеда плоскостью
В зависимости от расположения секущей плоскости и параллелепипеда сечение параллелепипеда может быть треугольником, четырехугольником, пятиугольником и шестиугольником.
Примечания
- ↑ [https://web.archive.org/web/20190424090245/http://lingvowiki.info/w/%D0%9A%D0%BD%D0%B8%D0%B3%D0%B8/%D0%94%D1%80%D0%B5%D0%B2%D0%BD%D0%B5%D0%B3%D1%80%D0%B5%D1%87%D0%B5%D1%81%D0%BA%D0%BE-%D1%80%D1%83%D1%81%D1%81%D0%BA%D0%B8%D0%B9_%D1%81%D0%BB%D0%BE%D0%B2%D0%B0%D1%80%D1%8C_%D0%94%D0%B2%D0%BE%D1%80%D0%B5%D1%86%D0%BA%D0%BE%D0%B3%D0%BE/96 Архивная копия от 24 апреля 2019 на Wayback Machine Древнегреческо-русский словарь Дворецкого «παραλληλεπίπεδον»
- ↑ Гусятников П.Б., Резниченко С.В. Векторная алгебра в примерах и задачах. — М.: Высшая школа, 1985. — 232 с.
