Интеграл

Разделы:

У этого термина существуют и другие значения, см. Интеграл (значения).

Интеграл — одно из важнейших понятий математического анализа, которое возникает при решении задач:

о нахождении площади под кривой;
пройденного пути при неравномерном движении;
массы неоднородного тела, и тому подобных;
а также в задаче о восстановлении функции по её производной (неопределённый интеграл)[1].

Упрощённо интеграл можно представить как аналог суммы для бесконечного числа бесконечно малых слагаемых. В зависимости от пространства, на котором задана подынтегральная функция, интеграл может быть — двойной, тройной, криволинейный, поверхностный и так далее; также существуют разные подходы к определению интеграла — различают интегралы Римана, Лебега, Стилтьеса и другие[2].

Содержание

1 Интеграл функции одной переменной
- 1.1 Неопределённый интеграл
- 1.2 Определённый интеграл
2 Интеграл в пространствах большей размерности
3 Применение
4 Обобщения
- 4.1 Интеграл Лебега
5 Историческая справка
6 См. также
7 Примечания
8 Литература
9 Ссылки

Интеграл функции одной переменной

Неопределённый интеграл

Основная статья: Неопределённый интеграл

Пусть дана f(x){displaystyle f(x)}

$f(x)$ — функция действительной переменной.Неопределённым интегралом функции f(x){displaystyle f(x)} $f(x)$ , или её первообразной, называется такая функция F(x){displaystyle F(x)} $F(x)$ , производная которой равна f(x){displaystyle f(x)} $f(x)$ , то есть F′(x)=f(x){displaystyle F'(x)=f(x)} $F'(x)=f(x)$ . Обозначается это так:

F(x)=∫f(x)dx{displaystyle F(x)=int f(x)dx}

{displaystyle F(x)=int f(x)dx}

В этой записи ∫{displaystyle int }

$int$ — знак интеграла, f(x){displaystyle f(x)} $f(x)$ называется подынтегральной функцией, а dx{displaystyle dx} $dx$ — элементом интегрирования.

Первообразная существует не для любой функции. Легко показать, что по крайней мере все непрерывные функции имеют первообразную.Поскольку производные двух функций, отличающихся на константу, совпадают, в выражение для неопределённого интеграла включают произвольную постоянную C{displaystyle C}

$C$ , например

∫x2dx=x33+C,∫cos⁡(x)dx=sin⁡(x)+C{displaystyle int x^{2}dx={frac {x^{3}}{3}}+C,qquad int cos(x)dx=sin(x)+C}

{displaystyle int x^{2}dx={frac {x^{3}}{3}}+C,qquad int cos(x)dx=sin(x)+C}

Операция нахождения интеграла называется интегрированием. Операции интегрирования и дифференцирования обратны друг другу в следующем смысле:

ddx∫f(x)dx=f(x),∫df(x)dxdx=f(x)+C{displaystyle {frac {d}{dx}}int f(x)dx=f(x),qquad int {frac {df(x)}{dx}}dx=f(x)+C}

{displaystyle {frac {d}{dx}}int f(x)dx=f(x),qquad int {frac {df(x)}{dx}}dx=f(x)+C}

Определённый интеграл

Основная статья: Определённый интеграл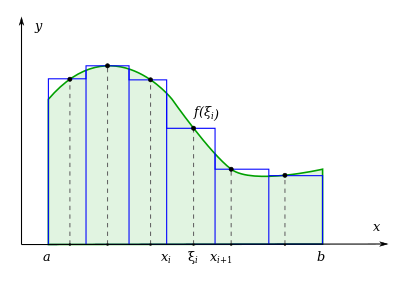 Интеграл как площадь криволинейной трапеции

Понятие определённого интеграла возникает в связи с задачей о нахождении площади криволинейной трапеции, нахождении пути по известной скорости при неравномерном движении и т. п.

Что такое интеграл, анимация

Рассмотрим фигуру, ограниченную осью абсцисс, прямыми x=a{displaystyle x=a}

$x=a$ и x=b{displaystyle x=b} $x=b$ и графиком функции y=f(x){displaystyle y=f(x)} $y=f(x)$ , называемую криволинейной трапецией (см. рисунок). Если по оси абсцисс отложено время, а по оси ординат — скорость тела, то площадь криволинейной трапеции есть пройденный телом путь.

Для вычисления площади этой фигуры естественно применить следующий приём. Разобьём отрезок [a;b]{displaystyle [a;b]}

$[a;b]$ на меньшие отрезки точками xi{displaystyle x_{i}} $x_{i}$ ,такими что a=x0<…<xi<xi+1<…<xn=b{displaystyle a=x_{0}<…<x_{i}<x_{i+1}<…<x_{n}=b} ${displaystyle a=x_{0}<...<x_{i}<x_{i+1}<...<x_{n}=b}$ ,а саму трапецию — на ряд узких полосок, лежащих над отрезками [xi;xi+1]{displaystyle [x_{i};x_{i+1}]} ${displaystyle [x_{i};x_{i+1}]}$ . Возьмём в каждом отрезке по произвольной точке ξi∈[xi;xi+1]{displaystyle xi _{i}in [x_{i};x_{i+1}]} ${displaystyle xi _{i}in [x_{i};x_{i+1}]}$ . Ввиду того, что длина i{displaystyle i} $i$ -го отрезка Δxi=xi+1−xi{displaystyle Delta x_{i}=x_{i+1}-x_{i}} ${displaystyle Delta x_{i}=x_{i+1}-x_{i}}$ мала, будем считать значение функции f(x){displaystyle f(x)} $f(x)$ на нём примерно постоянным и равным yi=f(ξi){displaystyle y_{i}=f(xi _{i})} ${displaystyle y_{i}=f(xi _{i})}$ . Площадь криволинейной трапеции будет приблизительно равна площади ступенчатой фигуры, изображённой на рисунке:

S≈∑i=0n−1yiΔxi(∗){displaystyle Sapprox sum _{i=0}^{n-1}y_{i}Delta x_{i}qquad (*)}

{displaystyle Sapprox sum _{i=0}^{n-1}y_{i}Delta x_{i}qquad (*)}

Если же теперь увеличивать число точек разбиения, так, чтобы длины всех отрезков неограниченно убывали (maxΔxi→0{displaystyle max Delta x_{i}to 0}

${displaystyle max Delta x_{i}to 0}$ ), площадь ступенчатой фигуры будет всё ближе к площади криволинейной трапеции.

Поэтому мы приходим к такому определению:

Если существует, независимо от выбора точек разбиения отрезка и точек ξi{displaystyle xi _{i}}

$xi _{i}$ , предел суммы (*) при стремлении длин всех отрезков к нулю, то такой предел называется определённым интегралом (в смысле Римана) от функции f(x){displaystyle f(x)} $f(x)$ по отрезку [a;b]{displaystyle [a;b]} $[a;b]$ и обозначается

∫abf(x)dx{displaystyle int limits _{a}^{b}f(x)dx}

{displaystyle int limits _{a}^{b}f(x)dx}

Сама функция при этом называется интегрируемой (в смысле Римана) на отрезке [a;b]{displaystyle [a;b]}

$[a;b]$ . Суммы вида (*) называются интегральными суммами.

Примеры интегрируемых функций:

непрерывные функции
функции, имеющие лишь конечное число разрывов первого рода
монотонные функции.

Пример неинтегрируемой функции: функция Дирихле (1 при x{displaystyle x}

$x$ рациональном, 0 при иррациональном). Поскольку множество рациональных чисел всюду плотно в R{displaystyle {mathbb {R} }} ${displaystyle {mathbb {R} }}$ , выбором точек ξi{displaystyle xi _{i}} $xi _{i}$ можно получить любое значение интегральных сумм от 0 до b−a{displaystyle b-a} $b-a$ .

Между определённым и неопределённым интегралом имеется простая связь. А именно, если

∫f(x)dx=F(x)+C{displaystyle int f(x)dx=F(x)+C}

{displaystyle int f(x)dx=F(x)+C}

то

∫abf(x)dx=F(b)−F(a){displaystyle int limits _{a}^{b}f(x)dx=F(b)-F(a)}

{displaystyle int limits _{a}^{b}f(x)dx=F(b)-F(a)}

Это равенство называется формулой Ньютона-Лейбница.

Интеграл в пространствах большей размерности

Двойные и кратные интегралы

Основная статья: Двойной интеграл Двойной интеграл как объём цилиндрического бруса

Понятие двойного интеграла возникает при вычислении объёма цилиндрического бруса,подобно тому, как определённый интеграл связан с вычислением площади криволинейной трапеции.Рассмотрим некоторую двумерную фигуру D{displaystyle D}

$D$ на плоскости XY{displaystyle XY} $XY$ и заданную на ней функцию двух переменных f(x,y){displaystyle f(x,y)} $f(x,y)$ .Понимая эту функцию как высоту в данной точке, поставим вопрос о нахождении объёма получившегося тела (см. рисунок).По аналогии с одномерным случаем, разобьём фигуру D{displaystyle D} $D$ на достаточно малые области di{displaystyle d_{i}} $d_{i}$ ,возьмём в каждой по точке ξi=(xi,yi){displaystyle xi _{i}=(x_{i},y_{i})} ${displaystyle xi _{i}=(x_{i},y_{i})}$ и составим интегральную сумму

∑if(xi,yi)S(di){displaystyle sum _{i}f(x_{i},y_{i})S(d_{i})}

{displaystyle sum _{i}f(x_{i},y_{i})S(d_{i})}

где S(di){displaystyle S(d_{i})}

${displaystyle S(d_{i})}$ — площадь области di{displaystyle d_{i}} $d_{i}$ . Если существует, независимо от выбора разбиения и точек ξi{displaystyle xi _{i}} $xi _{i}$ ,предел этой суммы при стремлении диаметров областей к нулю, то такой предел называется двойным интегралом(в смысле Римана) от функции f(x,y){displaystyle f(x,y)} $f(x,y)$ по области D{displaystyle D} $D$ и обозначается

∫Df(x,y)dS{displaystyle int limits _{D}f(x,y)dS}

{displaystyle int limits _{D}f(x,y)dS}

, ∫Df(x,y)dxdy{displaystyle int limits _{D}f(x,y)dxdy}

{displaystyle int limits _{D}f(x,y)dxdy}

, или ∬Df(x,y)dxdy{displaystyle iint limits _{D}f(x,y)dxdy}

{displaystyle iint limits _{D}f(x,y)dxdy}

Объём цилиндрического бруса равен этому интегралу.

Криволинейный интеграл

Основная статья: Криволинейный интеграл

Поверхностный интеграл

Основная статья: Поверхностный интеграл

Применение

К понятию интеграла естественным образом приводит также задача о массе неоднородного тела.Так, масса тонкого стержня с переменной плотностью ρ(x){displaystyle rho (x)}

$rho (x)$ даётся интегралом

M=∫ρ(x)dx{displaystyle M=int rho (x)dx}

{displaystyle M=int rho (x)dx}

в аналогичном случае плоской фигуры

M=∬ρ(x,y)dxdy{displaystyle M=iint rho (x,y)dxdy}

{displaystyle M=iint rho (x,y)dxdy}

и для трёхмерного тела

M=∭ρ(x,y,z)dxdydz{displaystyle M=iiint rho (x,y,z)dxdydz}

{displaystyle M=iiint rho (x,y,z)dxdydz}

Обобщения

Интеграл Лебега

Основная статья: Интеграл Лебега

В основе определения интеграла Лебега лежит понятие σ{displaystyle sigma }

$sigma$ -аддитивной меры.Мера является естественным обобщением понятий длины, площади и объёма.

Интеграл Лебега функции f{displaystyle f}

$f$ определённой на пространстве X{displaystyle X} $X$ по мере μ{displaystyle mu } $mu$ обозначают

∫Xfμ{displaystyle int limits _{X}fmu }

{displaystyle int limits _{X}fmu }

, ∫x∈Xf(x)μ{displaystyle int limits _{xin X}f(x)mu }

{displaystyle int limits _{xin X}f(x)mu }

или ∫Xf(x)μ(dx){displaystyle int limits _{X}f(x)mu (dx)}

{displaystyle int limits _{X}f(x)mu (dx)}

последнее два обозначения употребляют если необходимо подчеркнуть что интегрирование ведётся по переменной x{displaystyle x}

$x$ .Однако часто пользуются следующим не вполне правильным обозначением

∫Xfdμ.{displaystyle int limits _{X}fdmu .}

{displaystyle int limits _{X}fdmu .}

Полагая меру отрезка (прямоугольника, параллелепипеда) равной его длине (площади, объёму), а меру конечного либо счётного объединения непересекающихся отрезков (прямоугольников, параллелепипедов), соответственно, сумме их мер, и продолжая эту меру на более широкий класс измеримых множеств, получим т. наз. Лебегову меру на прямой (в R2{displaystyle {mathbb {R} }^{2}}

${displaystyle {mathbb {R} }^{2}}$ , в R3){displaystyle {mathbb {R} }^{3})} ${displaystyle {mathbb {R} }^{3})}$ .

Естественно, в этих пространствах возможно ввести и другие меры, отличные от Лебеговой. Меру можно ввести также на любом абстрактном множестве.В отличие от интеграла Римана, определение интеграла Лебега остаётся одинаковым для всех случаев.Идея его состоит в том, что при построении интегральной суммы значения аргумента группируются не по близости к друг другу (как в определении по Риману), а по близости соответствующих им значений функции.

Пусть есть некоторое множество X{displaystyle X}

$X$ , на котором задана σ{displaystyle sigma } $sigma$ -аддитивная мера μ{displaystyle mu } $mu$ , и функция f:X→R{displaystyle f:Xto {mathbb {R} }} ${displaystyle f:Xto {mathbb {R} }}$ .При построении интеграла Лебега рассматриваются только измеримые функции, то есть такие, для которых множества

Ea={x∈X:f(x)<a}{displaystyle E_{a}={xin X:f(x)<a}}

{displaystyle E_{a}={xin X:f(x)<a}}

измеримы для любого a∈R{displaystyle ain {mathbb {R} }}

${displaystyle ain {mathbb {R} }}$ (это эквивалентно измеримости прообраза любого борелевского множества).

Сначала интеграл определяется для ступенчатых функций, то есть таких, которые принимают конечное или счётное число значений ai{displaystyle a_{i}}

$a_{i}$ :

∫Xfμ=∑iaiμ(f−1(ai)){displaystyle int limits _{X}fmu =sum _{i}a_{i}mu (f^{-1}(a_{i}))}

{displaystyle int limits _{X}fmu =sum _{i}a_{i}mu (f^{-1}(a_{i}))}

где f−1(ai){displaystyle f^{-1}(a_{i})}

${displaystyle f^{-1}(a_{i})}$ — полный прообраз точки ai{displaystyle a_{i}} $a_{i}$ ; эти множества измеримы в силу измеримости функции. Если этот ряд абсолютно сходится, ступенчатую функцию f{displaystyle f} $f$ назовём интегрируемой в смысле Лебега.Далее, назовём произвольную функцию f{displaystyle f} $f$ интегрируемой в смысле Лебега, если существует последовательность интегрируемых ступенчатых функций fn{displaystyle f_{n}} $f_n$ , равномерно сходящаяся к f{displaystyle f} $f$ . При этом последовательность их интегралов также сходится; её предел и будем называть интегралом Лебега от функции f{displaystyle f} $f$ по мере μ{displaystyle mu } $mu$ :

∫Xfμ=lim∫Xfnμ{displaystyle int limits _{X}fmu =lim int limits _{X}f_{n}mu }

{displaystyle int limits _{X}fmu =lim int limits _{X}f_{n}mu }

Если рассматривать функции на Rn{displaystyle {mathbb {R} }^{n}}

${displaystyle {mathbb {R} }^{n}}$ и интеграл по мере Лебега, то все функции, интегрируемые в смысле Римана, будут интегрируемы и в смысле Лебега.Обратное же неверно (например, функция Дирихле не интегрируема по Риману, но интегрируема по Лебегу, так как равна нулю почти всюду).Фактически, любая ограниченная измеримая функция интегрируема по Лебегу.

Историческая справка

Основные понятия интегрального исчисления введены в работах Ньютона и Лейбница в конце XVII века (первые публикации состоялись в 1675 году). Лейбницу принадлежит обозначение интеграла ∫ydx{displaystyle int ydx}

${displaystyle int ydx}$ , напоминающее об интегральной сумме, как и сам символ ∫{displaystyle int } $int$ , от буквы ſ («длинная s») — первой буквы в латинском слове summa (тогда ſumma, сумма)[3]. Сам термин «интеграл» предложен Иоганном Бернулли, учеником Лейбница. Обозначение пределов интегрирования в виде ∫ab{displaystyle int _{a}^{b}} $int _{a}^{b}$ введено Фурье в 1820 году.

Строгое определение интеграла для случая непрерывных функций сформулировано Коши в 1823 году, а для произвольных функций — Риманом в 1853 году.Определение интеграла в смысле Лебега впервые дано Лебегом в 1902 году (для случая функции одной переменной и меры Лебега).

См. также

Примечания

↑ Интеграл // Казахстан. Национальная энциклопедия (рус.). — Алматы: Қазақ энциклопедиясы, 2005. — Т. II. — ISBN 9965-9746-3-2. (CC BY-SA 3.0)
↑ Большая российская энциклопедия : [в 35 т.] / гл. ред. Ю. С. Осипов. — М. : Большая российская энциклопедия, 2004—2017.
↑ Florian Cajori. A history of mathematical notations. — Courier Dover Publications, 1993. — P. 203. — 818 p. — (Dover books on mathematics). — ISBN 9780486677668.

Литература

Виноградов И. М. (гл. ред.). Интеграл // Математическая энциклопедия. — М., 1977. — Т. 2.
Фихтенгольц Г. М. Курс дифференциального и интегрального исчисления. — М.: Наука, 1969.
Колмогоров А. Н., Фомин С. В. Элементы теории функций и функционального анализа. — М.: Наука, 1976.

Ссылки

Интеграл:

Weisstein, Eric W. Integral (англ.) на сайте Wolfram MathWorld.
Wolfram Integrator — вычисление интегралов онлайн с помощью системы Mathematica
«Интеграл как умножение» — перевод статьи A Calculus Analogy: Integrals as Multiplication | BetterExplained (англ.)