Дивергенция

• Разделы:
  • Определение в декартовых координатах
  • Физическая интерпретация
  • Геометрическая интерпретация
  • Дивергенция в физике
  • Свойства
  • Дивергенция в ортогональных криволинейных координатах
  • Дивергенция в произвольных криволинейных координатах и её обобщение
  • См. также

У этого термина существуют и другие значения, см. Дивергенция (значения).

Диверге́нция (от лат. divergere — обнаруживать расхождение) — дифференциальный оператор, отображающий векторное поле на скалярное (то есть, в результате применения к векторному полю операции дифференцирования получается скалярное поле), который определяет (для каждой точки), «насколько расходится входящее и исходящее из малой окрестности данной точки поле», точнее, насколько расходятся входящий и исходящий потоки.

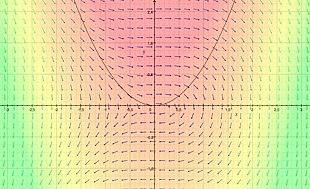Векторная функция и её дивергенция, представленные в виде скалярного поля (красный цвет указывает на повышение, зелёный обозначает уменьшение

Содержание

• 1 Определение
• 2 Определение в декартовых координатах
• 3 Физическая интерпретация
• 4 Геометрическая интерпретация
• 5 Дивергенция в физике
• 6 Свойства
• 7 Дивергенция в ортогональных криволинейных координатах
  • 7.1 Цилиндрические координаты
  • 7.2 Сферические координаты
  • 7.3 Параболические координаты
  • 7.4 Эллиптические координаты
• 8 Дивергенция в произвольных криволинейных координатах и её обобщение
  • 8.1 Свойства дивергенции тензора
• 9 См. также

Определение

Определение дивергенции выглядит так:

divF=limV→0Φ FV,{displaystyle operatorname {div} ,mathbf {F} =lim _{Vrightarrow 0}{{mathit {Phi }}_{ mathbf {F} } over V},} 

где ΦF{displaystyle Phi _{mathbf {F} }}

  — поток векторного поля F{displaystyle F}  через сферическую поверхность площадью S{displaystyle S} , ограничивающую объём V{displaystyle V} . Ещё более общим, а потому удобным в применении, является определение, когда форма области с поверхностью S{displaystyle S}  и объёмом V{displaystyle V}  допускается любой. Единственным требованием является её нахождение внутри сферы радиусом, стремящимся к нулю (то есть чтобы вся поверхность находилась в бесконечно малой окрестности данной точки, что нужно, чтобы дивергенция была локальной операцией и для чего очевидно недостаточно стремления к нулю площади поверхности и объёма её внутренности). В обоих случаях подразумевается, что

Φ F=∬S⊂⊃(F→,dS→).{displaystyle {mathit {Phi }}_{ mathbf {F} }=iint limits _{S}!!!!!!!!!!!subset !supset ;({vec {F}},d{vec {S}}).} 

Это определение, в отличие от приводимого ниже, не привязано к определённым координатам, например, к декартовым, что может представлять дополнительное удобство в определённых случаях. (Например, если выбирать окрестность в форме куба или параллелепипеда, легко получаются формулы для декартовых координат).

Определение легко и прямо обобщается на любую размерность n{displaystyle n}

  пространства: при этом под объёмом понимается n{displaystyle n} -мерный объём, а под площадью поверхности (n−1{displaystyle n-1} )-мерная площадь (гипер)поверхности соответствующей размерности.

Определение в декартовых координатах

Допустим, что векторное поле дифференцируемо в некоторой области. Тогда в трёхмерном декартовом пространстве дивергенция будет определяться выражением

divF=∂Fx∂x+∂Fy∂y+∂Fz∂z   {displaystyle operatorname {div} ,mathbf {F} ={frac {partial F_{x}}{partial x}}+{frac {partial F_{y}}{partial y}}+{frac {partial F_{z}}{partial z}} } 

(здесь F — обозначено некое векторное поле с декартовыми компонентамиFx,Fy,Fz{displaystyle F_{x},F_{y},F_{z}}

 ):

Это же выражение можно записать с использованием оператора набла

divF=∇⋅F   {displaystyle operatorname {div} ,mathbf {F} =nabla cdot mathbf {F} } 

Многомерная, а также двумерная и одномерная, дивергенция определяется в декартовых координатах в пространствах соответствующей размерности совершенно аналогично (в верхней формуле меняется лишь количество слагаемых, а нижняя остается той же, подразумевая оператор набла подходящей размерности).

Физическая интерпретация

С точки зрения физики (и в строгом смысле, и в смысле интуитивного физического образа математической операции) дивергенция векторного поля является показателем того, в какой степени данная точка пространства (точнее достаточно малая окрестность точки) является источником или стоком этого поля:

divF>0{displaystyle operatorname {div} ,mathbf {F} >0}  — точка поля является источником;

divF<0{displaystyle operatorname {div} ,mathbf {F} <0}  — точка поля является стоком;

divF=0{displaystyle operatorname {div} ,mathbf {F} =0}  — стоков и источников нет, либо они компенсируют друг друга.

Простым, хоть быть может и несколько схематическим, примером может служить озеро (для простоты — постоянной единичной глубины со всюду горизонтальной скоростью течения воды, не зависящей от глубины, давая, таким образом, двумерное векторное поле на двумерном пространстве). Если угодно иметь более реалистическую картину, то можно рассмотреть горизонтальную проекцию скорости, проинтегрированную по вертикальной пространственной координате, что даст ту же картину двумерного векторного поля на двумерном пространстве, причём картина качественно будет для наших целей не сильно отличаться от упрощённой первой, количественно же являться её обобщением (весьма реалистическим). В такой модели (и в первом, и во втором варианте) родники, бьющие из дна озера, будут давать положительную дивергенцию поля скоростей течения, а подводные стоки (пещеры, куда вода утекает) — отрицательную дивергенцию.

Дивергенция вектора плотности тока даёт минус скорость накопления заряда в электродинамике (так как заряд сохраняется, то есть не исчезает и не появляется, а может только переместиться через границы какого-то объёма, чтобы накопиться в нём или уйти из него; а если и возникают или исчезают где-то положительные и отрицательные заряды — то только в равных количествах). (См. Уравнение непрерывности).

Геометрическая интерпретация

Если в качестве векторного поля (на двумерном пространстве) взять совокупность направлений наискорейшего спуска на земной поверхности, то дивергенция покажет местоположение вершин и впадин, причём на вершинах дивергенция будет положительна (направления спуска расходятся от вершин), а на впадинах отрицательная (ко впадинам направления спуска сходятся).

Дивергенция в физике

Дивергенция — одна из наиболее широко употребимых в физике операций. Представляет собой одно из достаточно немногих базовых понятий теоретической физики и является одним из базовых элементов физического языка.

В стандартной формулировке классической теории поля дивергенция занимает центральное место (в альтернативных формулировках может не находиться в самом центре изложения, но всё равно остается важным техническим инструментом и важной идеей).

В электродинамике дивергенция входит в качестве главной конструкции в два из четырёх уравнений Максвелла. Основное уравнение теории ньютоновской гравитации в полевом виде также содержит в качестве основной конструкции дивергенцию (напряженности гравитационного поля). В тензорных теориях гравитации (включая ОТО, и имея в виду в первую очередь её) основное полевое уравнение (в ОТО, но как правило — так или иначе — и в альтернативных современных теориях тоже) также включает в себя дивергенцию в некотором обобщении. То же можно сказать о классической (то есть неквантовой) теории практически любого из фундаментальных полей, как экспериментально известных, так и гипотетических.

Помимо этого, как видно из приведённых выше примеров, дивергенция применима и в чисто геометрическом плане, а также — особенно часто — к различным материальным потокам (дивергенция скорости течения жидкости или газа, дивергенция плотности электрического тока и т. п.).

Свойства

Следующие свойства могут быть получены из обычных правил дифференцирования.

• Линейность: для любых векторных полей F и G и для всех вещественных чисел a и b

div⁡(aF+bG)=adiv⁡(F)+bdiv⁡(G){displaystyle operatorname {div} (amathbf {F} +bmathbf {G} )=a;operatorname {div} (mathbf {F} )+b;operatorname {div} (mathbf {G} )} 

• Если φ — скалярное поле, а F — векторное, тогда:

div⁡(φF)=grad⁡(φ)⋅F+φdiv⁡(F),{displaystyle operatorname {div} (varphi mathbf {F} )=operatorname {grad} (varphi )cdot mathbf {F} +varphi ;operatorname {div} (mathbf {F} ),}  или

∇⋅(φF)=(∇φ)⋅F+φ(∇⋅F).{displaystyle nabla cdot (varphi mathbf {F} )=(nabla varphi )cdot mathbf {F} +varphi ;(nabla cdot mathbf {F} ).} 

• Свойство, связывающее векторные поля F и G, заданные в трёхмерном пространстве, с ротором:

div⁡(F×G)=rot⁡(F)⋅G−F⋅rot⁡(G),{displaystyle operatorname {div} (mathbf {F} times mathbf {G} )=operatorname {rot} (mathbf {F} )cdot mathbf {G} ;-;mathbf {F} cdot operatorname {rot} (mathbf {G} ),}  или

∇⋅(F×G)=(∇×F)⋅G−F⋅(∇×G).{displaystyle nabla cdot (mathbf {F} times mathbf {G} )=(nabla times mathbf {F} )cdot mathbf {G} -mathbf {F} cdot (nabla times mathbf {G} ).} 

• Дивергенция от градиента есть лапласиан:

div⁡(grad⁡(φ))=Δφ{displaystyle operatorname {div} (operatorname {grad} (varphi ))=Delta varphi } 

• Дивергенция от ротора:

div⁡(rot⁡(F))=0{displaystyle operatorname {div} (operatorname {rot} (mathbf {F} ))=0} 

Дивергенция в ортогональных криволинейных координатах

div⁡(A)=div⁡(q1A1+q2A2+q3A3)={displaystyle operatorname {div} (mathbf {A} )=operatorname {div} (mathbf {q_{1}} A_{1}+mathbf {q_{2}} A_{2}+mathbf {q_{3}} A_{3})=} 

=1H1H2H3[∂∂q1(A1H2H3)+∂∂q2(A2H3H1)+∂∂q3(A3H1H2)]{displaystyle ={frac {1}{H_{1}H_{2}H_{3}}}left[{frac {partial }{partial q_{1}}}(A_{1}H_{2}H_{3})+{frac {partial }{partial q_{2}}}(A_{2}H_{3}H_{1})+{frac {partial }{partial q_{3}}}(A_{3}H_{1}H_{2})right]}

 , где Hi{displaystyle H_{i}}  — коэффициенты Ламе.

Цилиндрические координаты

Коэффициенты Ламе:

Hr=1;Hθ=r;Hz=1.{displaystyle {begin{matrix}H_{r}=1;H_{theta }=r;H_{z}=1.end{matrix}}} 

Отсюда:

div⁡A(r,θ,z)=1r∂∂r(Arr)+1r∂∂θ(Aθ)+∂∂z(Az){displaystyle operatorname {div} mathbf {A} (r,theta ,z)={frac {1}{r}}{frac {partial }{partial r}}(A_{r}r)+{frac {1}{r}}{frac {partial }{partial theta }}(A_{theta })+{frac {partial }{partial z}}(A_{z})} 

Сферические координаты

Коэффициенты Ламе:

Hr=1;Hθ=r;Hϕ=rsin⁡θ.{displaystyle {begin{matrix}H_{r}=1;H_{theta }=r;H_{phi }=rsin {theta }.end{matrix}}} 

Отсюда:

div⁡A(r,θ,ϕ)=1r2∂∂r[Arr2]+1rsin⁡θ∂∂θ[Aθsin⁡θ]+1rsin⁡θ∂∂ϕ[Aϕ]{displaystyle operatorname {div} mathbf {A} (r,theta ,phi )={frac {1}{r^{2}}}{frac {partial }{partial r}}left[A_{r}r^{2}right]+{frac {1}{rsin {theta }}}{frac {partial }{partial theta }}left[A_{theta }sin {theta }right]+{frac {1}{rsin {theta }}}{frac {partial }{partial phi }}{big [}A_{phi }{big ]}} 

Параболические координаты

Коэффициенты Ламе:

Hξ=ξ+η2ξ;Hη=ξ+η2η;Hϕ=ηξ{displaystyle {begin{matrix}H_{xi }={frac {sqrt {xi +eta }}{2{sqrt {xi }}}};H_{eta }={frac {sqrt {xi +eta }}{2{sqrt {eta }}}};H_{phi }={sqrt {eta xi }}end{matrix}}} .

Отсюда:

div⁡A(ξ,η,ϕ)=4ξ+η∂∂ξ[Aξξ2+ξη2]+4ξ+η∂∂η[Aηη2+ξη2]+1ξη∂∂ϕ[Aϕ]{displaystyle operatorname {div} mathbf {A} (xi ,eta ,phi )={frac {4}{xi +eta }}{frac {partial }{partial xi }}left[A_{xi }{frac {sqrt {xi ^{2}+xi eta }}{2}}right]+{frac {4}{xi +eta }}{frac {partial }{partial eta }}left[A_{eta }{frac {sqrt {eta ^{2}+xi eta }}{2}}right]+{frac {1}{sqrt {xi eta }}}{frac {partial }{partial phi }}{Big [}A_{phi }{Big ]}} 

Эллиптические координаты

Коэффициенты Ламе:

Hξ=σξ2−η2ξ2−1Hη=σξ2−η21−η2Hϕ=σ(ξ2−1)(1−η2){displaystyle {begin{matrix}H_{xi }=sigma {sqrt {frac {xi ^{2}-eta ^{2}}{xi ^{2}-1}}}H_{eta }=sigma {sqrt {frac {xi ^{2}-eta ^{2}}{1-eta ^{2}}}}H_{phi }=sigma {sqrt {(xi ^{2}-1)(1-eta ^{2})}}end{matrix}}} .

Отсюда:

div⁡A(ξ,η,ϕ)=1σ(ξ2−η2)∂∂ξ[Aξ(ξ2−η2)(ξ2−1)]+{displaystyle operatorname {div} mathbf {A} (xi ,eta ,phi )={frac {1}{sigma (xi ^{2}-eta ^{2})}}{frac {partial }{partial xi }}left[A_{xi }{sqrt {(xi ^{2}-eta ^{2})(xi ^{2}-1)}}right]+} 

1σ(ξ2−η2)∂∂η[Aη(ξ2−η2)(1−η2)]+1σ(ξ2−1)(1−η2)∂∂ϕ[Aϕ]{displaystyle {frac {1}{sigma (xi ^{2}-eta ^{2})}}{frac {partial }{partial eta }}left[A_{eta }{sqrt {(xi ^{2}-eta ^{2})(1-eta ^{2})}}right]+{frac {1}{sigma {sqrt {(xi ^{2}-1)(1-eta ^{2})}}}}{frac {partial }{partial phi }}{Big [}A_{phi }{Big ]}} 

Дивергенция в произвольных криволинейных координатах и её обобщение

Формулу для дивергенции векторного поля в произвольных координатах (в любой конечной размерности) нетрудно получить из общего определения через предел отношения потока к объёму, воспользовавшись тензорной записью смешанного произведения и тензорной формулой объёма.

Существует обобщение операции дивергенции на действие не только на векторы, но и на тензоры более высокого ранга.

В общем случае дивергенция определяется ковариантной производной:

div=(∇⋅)=R→α∇α⋅{displaystyle operatorname {div} =(nabla cdot )={vec {R}}^{alpha }nabla _{alpha }cdot } , где R→α{displaystyle {vec {R}}^{alpha }}  — координатные векторы.

Это позволяет находить выражения для дивергенции в произвольных координатах для векторного:

∇⋅v→=R→α∇α⋅viR→i=∇ivi{displaystyle nabla cdot {vec {v}}={vec {R}}^{alpha }nabla _{alpha }cdot v^{i}{vec {R}}_{i}=nabla _{i}v^{i}} .

или тензорного поля:

∇⋅T=R→α∇α⋅TijR→iR→j=R→j∇iTij{displaystyle nabla cdot T={vec {R}}^{alpha }nabla _{alpha }cdot T^{ij}{vec {R}}_{i}{vec {R}}_{j}={vec {R}}_{j}nabla _{i}T^{ij}} .

В общем случае, дивергенция понижает ранг тензора на 1.

Свойства дивергенции тензора

∇⋅v→v→=v→∇⋅v→+(v→⋅∇)v→{displaystyle nabla cdot {vec {v}}{vec {v}}={vec {v}}nabla cdot {vec {v}}+left({vec {v}}cdot nabla right){vec {v}}} 

См. также

• Векторный анализ
• Теорема Остроградского — Гаусса
• Формулы векторного анализа