Трёхмерное схематичное изображение столбчатой диаграммы
Трёхмерное схематичное изображение столбчатой диаграммы
Диагра́мма (греч. Διάγραμμα (diagramma) — изображение, рисунок, чертёж) — графическое представление данных, позволяющее быстро оценить соотношение нескольких величин[1]. Представляет собой геометрическое символьное изображение информации с применением различных приёмов техники визуализации[2].
Иногда для оформления диаграмм используется трёхмерная визуализация, спроецированная на плоскость, что придаёт диаграмме отличительные черты или позволяет иметь общее представление об области, в которой она применяется. Например: финансовая диаграмма, связанная с денежными суммами, может представлять собой количество купюр в пачке или монет в стопке; диаграмма сравнения количества подвижного состава — различную длину изображённых поездов и т. д. Благодаря своей наглядности и удобству использования, диаграммы часто используются не только в повседневной работе бухгалтеров, логистов и других служащих, но и при подготовке материалов презентаций для клиентов и менеджеров различных организаций[3].
В различных процессорах графопостроения (графических программах) и электронных таблицах при изменении данных, на основе которых построена диаграмма, она будет автоматически перестроена с учётом внесённых изменений в таблицу исходных данных. Это позволяет быстро сравнивать различные показатели, статистические данные и т. д. — можно вводить новые данные и сразу видеть изменения диаграммы[4].
Основные типы диаграмм
Диаграммы в основном состоят из геометрических объектов (точек, линий, фигур различной формы и цвета) и вспомогательных элементов (осей координат, условных обозначений, заголовков и т. п.). Также диаграммы делятся на плоскостные (двумерные) и пространственные (трёхмерные или объёмные). Сравнение и сопоставление геометрических объектов на диаграммах может происходить по различным измерениям: по площади фигуры или её высоте, по местонахождению точек, по их густоте, по интенсивности цвета и т. д. Кроме того, данные могут быть представлены в прямоугольной или полярной системе координат[4].
Диаграммы-линии (графики)
 RSG-диаграмма (график)
RSG-диаграмма (график)
Диаграммы-линии или графики — это тип диаграмм, на которых полученные данные изображаются в виде точек, соединённых прямыми линиями. Точки могут быть как видимыми, так и невидимыми (ломаные линии). Также могут изображаться точки без линий (точечные диаграммы). Для построения диаграмм-линий применяют прямоугольную систему координат. Обычно по оси абсцисс откладывается время (годы, месяцы и т. д.), а по оси ординат — размеры изображаемых явлений или процессов. На осях наносят масштабы[3].
Диаграммы-линии целесообразно применять тогда, когда число размеров (уровней) в ряду велико. Кроме того, такие диаграммы удобно использовать, если требуется изобразить характер или общую тенденцию развития явления или явлений. Линии удобны и при изображении нескольких динамических рядов для их сравнения, когда требуется сравнение темпов роста. На одной диаграмме такого типа не рекомендуется помещать более трёх-четырёх кривых. Их большое количество может усложнить чертёж, и линейная диаграмма может потерять наглядность[5].
Основной недостаток диаграмм-линий — равномерная шкала, позволяющая измерить и сравнить только абсолютные приросты или уменьшения показателей в течение периода исследований. Относительные изменения показателей искажаются при изображении их с равномерной вертикальной шкалой. Также в такой диаграмме может быть невозможным изображение рядов динамики с резкими скачками уровней, которые требуют уменьшения масштаба диаграммы, и показатели в ней динамики более «спокойного» объекта теряют свою точность. Вероятность присутствия в этих типах диаграмм резких изменений показателей возрастает с увеличением длительности периода времён на графике[4].
Диаграммы-области
Диаграммы-области — это тип диаграмм, схожий с линейными диаграммами способом построения кривых линий. Отличается от них тем, что область под каждым графиком заполняется индивидуальным цветом или оттенком. Преимущество данного метода в том, что он позволяет оценивать вклад каждого элемента в рассматриваемый процесс. Недостаток это типа диаграмм также схож с недостатком обычных линейных диаграмм — искажение относительных изменений показателей динамики с равномерной шкалой ординат[6].
Столбчатые и линейные диаграммы (гистограммы)
 Сгруппированная столбчатая диаграмма
Сгруппированная столбчатая диаграмма
Классическими диаграммами являются столбчатые и линейные (полосовые) диаграммы. Также они называются гистограммами. Столбчатые диаграммы в основном используются для наглядного сравнения полученных статистических данных или для анализа их изменения за определённый промежуток времени. Построение столбчатой диаграммы заключается в изображении статистических данных в виде вертикальных прямоугольников или трёхмерных прямоугольных столбиков. Каждый столбик изображает величину уровня данного статистического ряда. Все сравниваемые показатели выражены одной единицей измерения, поэтому удаётся сравнить статистические показатели данного процесса[4].
Разновидностями столбчатых диаграмм являются линейные (полосовые) диаграммы. Они отличаются горизонтальным расположением столбиков.Столбчатые и линейные диаграммы взаимозаменяемы, рассматриваемые в них статистические показатели могут быть представлены как вертикальными, так и горизонтальными столбиками. В обоих случаях для изображения величины явления используется одно измерение каждого прямоугольника — высота или длина столбика. Поэтому и сфера применения этих двух диаграмм в основном одинакова[4].
Столбчатые диаграммы могут изображаться и группами (одновременно расположенными на одной горизонтальной оси с разной размерностью варьирующих признаков). Образующие поверхности столбчатых и линейных диаграмм могут представлять собой не только прямоугольники, но также квадраты, треугольники, трапеции и т. д.
Круговые (секторные) диаграммы
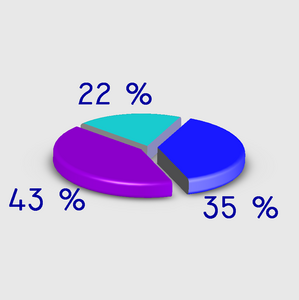
Достаточно распространённым способом графического изображения структуры статистических совокупностей является секторная диаграмма, так как идея целого очень наглядно выражается кругом, который представляет всю совокупность. Относительная величина каждого значения изображается в виде сектора круга, площадь которого соответствует вкладу этого значения в сумму значений. Этот вид графиков удобно использовать, когда нужно показать долю каждой величины в общем объёме. Сектора могут изображаться как в общем круге, так и отдельно, расположенными на небольшом удалении друг от друга.
Круговая диаграмма сохраняет наглядность только в том случае, если количество частей совокупности диаграммы небольшое. Если частей диаграммы слишком много, её применение неэффективно по причине несущественного различия сравниваемых структур.Недостаток круговых диаграмм — малая ёмкость, невозможность отразить более широкий объём полезной информации[4].
Радиальные (сетчатые) диаграммы
В отличие от линейных диаграмм, в радиальных или сетчатых диаграммах более двух осей. По каждой из них производится отсчёт от начала координат, находящегося в центре. Для каждого типа полученных значений создаётся своя собственная ось, которая исходит из центра диаграммы. Радиальные диаграммы напоминают сетку или паутину, поэтому иногда их называют сетчатыми.Преимущество радиальных диаграмм в том, что они позволяют отображать одновременно несколько независимых величин, которые характеризуют общее состояние структуры статистических совокупностей. Если отсчёт производить не с центра круга, а с окружности, то такая диаграмма будет называться спиральной диаграммой[4][7].
Картодиаграммы
Картодиаграммы — это сочетания диаграмм с географическими картами или схемами. В качестве изобразительных знаков в картодиаграммах используются обычные диаграммы (гистограммы, круговые, линейные), которые размещаются на контурах географических карт или на схемах каких-либо объектов. Картодиаграммы дают возможность географически отразить более сложные статистико-географические построения, чем обычные типы диаграмм.
Недостатком картодиаграмм могут служить сложности в рисовании контуров карт, а также значительная разница в размерах областей географических карт и размеров диаграмм на них.
Биржевые диаграммы
 График «Японские свечи» валютной пары доллар США—швейцарский франк
График «Японские свечи» валютной пары доллар США—швейцарский франк
Биржевые диаграммы отражают наборы данных из нескольких значений (например: цена открытия биржи, цена закрытия, максимальная и минимальная цена определённого временного интервала). Применяются для отображения биржевых данных: котировок акций или валют, данных спроса и предложения[8].
Пространственные (трёхмерные) диаграммы
Пространственные, или трёхмерные диаграммы являются объёмными аналогами пяти основных типов двухмерных диаграмм: линейных, диаграмм-областей, гистограмм (столбчатых и линейных), круговых. Изображение в объёмном виде упрощает понимание информации. Такие диаграммы выглядят убедительнее. Сложность в создании трёхмерных диаграмм заключается в правильности отображения согласно теме диаграммы.[9]
Ботанические диаграммы
См. также: Формула цветка Диаграмма цветка. 1 — ось соцветия, 2 — прицветник, 3 — чашелистик, 4 — лепесток, 5 — тычинка, 6 — гинецей, 7 — кроющий лист.
Диаграмма цветка. 1 — ось соцветия, 2 — прицветник, 3 — чашелистик, 4 — лепесток, 5 — тычинка, 6 — гинецей, 7 — кроющий лист.
Диаграмма цветка — схематическая проекция цветка на плоскость, перпендикулярную его оси и проходящую через кроющий лист и ось соцветия или побега, на котором сидит цветок. Она отражает число, относительные размеры и взаимное расположение частей цветка.
Построение диаграммы производится на основании поперечных разрезов бутона, так как при распускании цветка некоторые части могут опадать (например, чашелистики у маковых или околоцветник у винограда). Диаграмма ориентируется так, чтобы ось соцветия находилась вверху, а кроющий лист — внизу.
Обозначения на диаграмме цветка:
- Ось соцветия — точка (если цветок верхушечный, ось соцветия не изображается);
- Кроющий лист, прицветники и чашелистики — скобки с килем (фигурные скобки) различного размера;
- Лепестки — круглые скобки;
- Тычинки — почковидные фигуры, показывающие поперечный срез через пыльник (при большом числе тычинок возможно упрощенное изображение в виде затушёванного эллипса);
- Пестик — круги или овалы, отражающие поперечный разрез завязи; внутри завязи показывают семязачатки маленькими кружками на соответствующих частях плодолистиков.
- В случае срастания между собой частей цветка их значки на диаграмме соединяют линиями.
- Также могут быть показаны дополнительные элементы цветка, например, нектарники или диски.
В диаграмме цветка могут быть изображены либо только те части, которые видны на разрезе (эмпирическая диаграмма цветка), либо также (пунктиром) недоразвитые и исчезнувшие в процессе эволюции части (теоретическая диаграмма цветка, составляемая на основании изучения нескольких эмпирических диаграмм).
Диаграмма побега отражает схему поперечного разреза через вегетативную почку.
Анимированные диаграммы
В некоторых случаях стандартных свойств обычных неподвижных диаграмм и графиков бывает недостаточно. С целью повышения информативности, возникла идея: к обычным свойствам статичных диаграмм (формам, цветам, способам отображения и тематики) добавить свойство подвижности и изменения с течением времени. То есть представить диаграммы в виде определённых анимаций.
Группой исследователей из Массачусетского технологического института был найден способ отображения информации с помощью анимированных диаграмм. Разработанные ими диаграммы представляют собой анимированные интерактивные графики, работающие в режиме реального времени. В качестве примера разработки были взяты данные о поведении и действиях пользователей одного из сетевых ресурсов.
Под руководством Френсиса Лама (Francis Lam) исследователи создали два интерфейса анимированных диаграмм Seascape и Volcano. Характер изменений изображения на диаграммах свидетельствует о социальной активности пользователей ресурса. Например, размер квадратиков указывает на объём темы — чем больше площадь квадратика, тем больше объём обсуждаемой темы. Эти квадратики находятся в постоянном движении, представляющем собой, похожие на гармонические, колебания в плоскости диаграммы, смещающиеся линейно в какую-либо из сторон. По скорости движения можно судить об активности темы, а амплитуда колебаний показывает разницу во времени появления новых сообщений. В любой момент, наведя курсор в плоскость диаграммы, её можно остановить, выбрать интересующий квадратик и открыть тему, которой он соответствует. Открывающаяся в этом же окне тема, также представляет собой анимацию из кружочков, движущихся в разные стороны в пределах окна по типу Броуновского движения. Кружочки символизируют действия отдельных пользователей, и скорость их движения напрямую зависит от активности этих пользователей.
Seascape и Volcano отличаются друг от друга цветовой гаммой и количеством визуализированных данных. У Volcano, в отличие от Seascape отсутствуют волнообразные колебания.
По словам разработчиков, построение графиков с помощью анимированных диаграмм, должно позволить человеку быстрее воспринимать информацию с них путём привлечения внимания пользователя диаграммой и быстрой передачей данных в мозг. В данный момент ещё не приняты какие-либо требования или стандарты к генерации анимированных диаграмм[10].

Анимированная диаграмма с интерфейсом «Seascape»

Анимированная диаграмма с интерфейсом «Volcano»
Преимущества диаграмм
Преимущество диаграмм перед другими типами наглядной статистической информации заключается в том, что они позволяют быстро произвести логический вывод из большого количества полученных данных. Результаты расчётов, выполненных с помощью систем статистических вычислений, заносятся в таблицы. Они являются основой для последующего анализа или для подготовки статистического отчёта.
Сами по себе цифры в этих таблицах не являются достаточно наглядными, а если их много, они не производят достаточного впечатления. Кроме того, графическое изображение позволяет осуществить контроль достоверности полученных данных, так как на графике достаточно ярко проявляются возможные неточности, которые могут быть связаны с ошибками на каком-либо этапе проведения исследования. В основном все статистические пакеты позволяют графически предоставить полученную числовую информацию в виде различных диаграмм, а затем, если это необходимо, перенести их в текстовый редактор для сборки окончательного варианта статистического отчёта[4].
История возникновения диаграмм
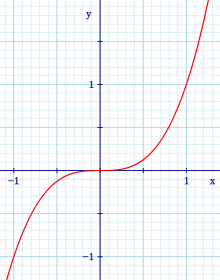 График функции f(x)=x3 {displaystyle f(x)={x^{3}}! }
График функции f(x)=x3 {displaystyle f(x)={x^{3}}! }
Во всех диаграммах используется функциональная зависимость как минимум двух типов данных. Соответственно, первыми диаграммами были обыкновенные графики функций, в которых допустимые значения аргумента соответствуют значениям функций.
Идеи функциональной зависимости использовались в древности. Она обнаруживается уже в первых математически выраженных соотношениях между величинами, а также в первых правилах действий над числами, в первых формулах для нахождения площади и объёма геометрических фигур. Вавилонские учёные, таким образом, несознательно установили, что площадь круга является функцией от его радиуса 4—5 тыс. лет назад[11]. Астрономические таблицы вавилонян, древних греков и индийцев — яркий пример табличного задания функции, а таблицы, соответственно, являются хранилищем данных для диаграмм.
В XVII веке французские учёные Франсуа Виет и Рене Декарт заложили основы понятия функции и разработали единую буквенную математическую символику, которая вскоре получила всеобщее признание. Также геометрические работы Декарта и Пьера Ферма проявили отчётливое представление переменной величины и прямоугольной системы координат — вспомогательных элементов всех современных диаграмм[11].
Первые статистические графики начал строить английский экономист У. Плейфер в работе «Коммерческий и политический атлас» 1786 года. Это произведение послужило толчком для развития графических методов в общественных науках[12].
См. также
В родственных проектах
- Гистограмма
- Японские свечи
- Диаграмма Ганта
- Кривая Парето
- Диаграмма связей
- Графика
- Визуализация
- Иллюстрация
- Графический дизайн
- Трёхмерная графика
- ДРАКОН (алгоритмический язык)
- UML-диаграммы
Примечания
- ↑ Значение слова «диаграмма» на Deport.ru
- ↑ Значение слова «диаграмма» на «Академике»
- ↑ 1 2 Назначение диаграмм
- ↑ 1 2 3 4 5 6 7 8 Способы наглядного представления результатов исследования. Графики и диаграммы
- ↑ «Диаграммы динамики»
- ↑ «Областные диаграммы»
- ↑ «Замкнутые и спиральные диаграммы»
- ↑ «Парус инвестора»
- ↑ «Почему трёхмерные диаграммы убедительнее»
- ↑ «Графики и диаграммы становятся подвижными»
- ↑ 1 2 «Исторические сюжеты о функциях»
- ↑ Теория статистики / под ред. Шмойловой Р. А. — третье издание, переработанное. — Москва: Финансы и статистика, 2002. — 560 с. — 5000 экз. — ISBN 5-279-01951-8.