Теория случайных блужданий — теория, согласно которой изменения стоимости ценных бумаг колеблются случайным образом вокруг своей объективной цены, оппонирует теории технического анализа.
Одномерное дискретное случайное блуждание
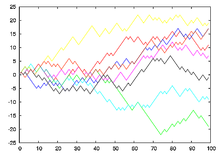 Графики Xi(i){displaystyle X_{i}(i)} восьми одномерных случайных блужданий.
Графики Xi(i){displaystyle X_{i}(i)} восьми одномерных случайных блужданий. Пример двумерного случайного блуждания. 229 шагов, длина шага от -0.5 до 0.5, равновероятные направления x{displaystyle x} или y{displaystyle y}.
Пример двумерного случайного блуждания. 229 шагов, длина шага от -0.5 до 0.5, равновероятные направления x{displaystyle x} или y{displaystyle y}.
Одномерное дискретное случайное блуждание — это случайный процесс с дискретным временем {Yn}n≥0{displaystyle {Y_{n}}_{ngeq 0}}, имеющий вид
- Yn=Y0+∑i=1nXi{displaystyle Y_{n}=Y_{0}+sum limits _{i=1}^{n}X_{i}},
где
- Y0{displaystyle Y_{0}} — начальное состояние;
- Xi={1,pi−1,qi≡1−pi,0<pi<1,i∈N{displaystyle X_{i}={begin{cases}1,&p_{i}\-1,&q_{i}equiv 1-p_{i}end{cases}},quad 0<p_{i}<1,quad iin mathbb {N} };
- случайные величины Y0,Xi,i=1,2,…{displaystyle Y_{0},X_{i},i=1,2,ldots } совместно независимы.
Случайное блуждание как цепь Маркова
Одномерное дискретное случайное блуждание является цепью Маркова с целыми состояниями, чьё начальное распределение задаётся функцией вероятности случайной величины X0{displaystyle X_{0}}, а матрица переходных вероятностей имеет вид
- P≡(pij)i,j∈Z=(⋱⋱⋱q−10p−1q00p0q10p1⋱⋱⋱){displaystyle Pequiv (p_{ij})_{i,jin mathbb {Z} }=left({begin{matrix}ddots &ddots &ddots &\&q_{-1}&0&p_{-1}&\&&q_{0}&0&p_{0}\&&&q_{1}&0&p_{1}\&&&&ddots &ddots &ddots end{matrix}}right)},
то есть
- pi,i+1≡P(Xn+1=i+1∣Xn=i)=pi,{displaystyle p_{i,i+1}equiv mathbb {P} (X_{n+1}=i+1mid X_{n}=i)=p_{i},}
- pi,i−1≡P(Xn+1=i−1∣Xn=i)=qi,i∈Z,{displaystyle p_{i,i-1}equiv mathbb {P} (X_{n+1}=i-1mid X_{n}=i)=q_{i},quad iin mathbb {Z} ,}
- pij≡P(Xn+1=j∣Xn=i)=0,|i−j|≠1.{displaystyle p_{ij}equiv mathbb {P} (X_{n+1}=jmid X_{n}=i)=0,quad |i-j|not =1.}
| Это заготовка статьи по математике. Вы можете помочь проекту, дополнив её. |

 восьми одномерных случайных блужданий.
восьми одномерных случайных блужданий. или y{displaystyle y}
или y{displaystyle y} .
. , имеющий вид
, имеющий вид ,
, — начальное состояние;
— начальное состояние; ;
; совместно независимы.
совместно независимы. , а матрица переходных вероятностей имеет вид
, а матрица переходных вероятностей имеет вид ,
,


