wiki

Гомотопические группы

Разделы:

Гомотопи́ческие гру́ппы — одно из основных понятий алгебраической топологии.

Содержание

1 Определение
2 Зависимость от начальной точки
3 Абелевость высших гомотопических групп
4 Относительные гомотопические группы и точная гомотопическая последовательность
5 История
6 См. также
7 Литература

Определение

Пусть X{displaystyle X}

$X$ — топологическое пространство, x0∈X{displaystyle x_{0}in X} $x_{0}in X$ ; In⊂Rn{displaystyle I^{n}subset mathbb {R} ^{n}} $I^{n}subset mathbb{R} ^{n}$ — единичный куб (In={(t1,t2,…tn):0⩽tn⩽1}{displaystyle I^{n}={(t_{1},t_{2},ldots t_{n}):0leqslant t_{n}leqslant 1}} ${displaystyle I^{n}={(t_{1},t_{2},ldots t_{n}):0leqslant t_{n}leqslant 1}}$ , ∂In{displaystyle partial I^{n}} $partial I^{n}$ — граница этого куба, то есть множество точек куба такое, что для некоторого i ti{displaystyle t_{i}} $t_{i}$ равен 0 или 1. Множество гомотопических классов [f]{displaystyle [f]} $[f]$ непрерывных отображений f:In→X{displaystyle fcolon I^{n}to X} , для которых f(∂In)=x0∈X{displaystyle f(partial I^{n})=x_{0}in X} $f(partial I^{n})=x_{0}in X$ обозначается πn(X,x0){displaystyle pi _{n}(X,x_{0})} $pi _{n}(X,x_{0})$ (причём ∂In{displaystyle partial I^{n}} $partial I^{n}$ переходит в точку x0{displaystyle x_{0}} $x_{0}$ при всех отображениях и гомотопиях). На этом множестве можно определить умножение элементов следующим образом:

[f][g]=[f∗g]{displaystyle [f][g]=[f*g]}

$[f][g]=[f*g]$ , где

f∗g(t1,t2,…tn)=f(2t1,t2,…tn){displaystyle f*g(t_{1},t_{2},ldots t_{n})=f(2t_{1},t_{2},ldots t_{n})}

$f*g(t_{1},t_{2},ldots t_{n})=f(2t_{1},t_{2},ldots t_{n})$ , если 0⩽t1⩽12{displaystyle 0leqslant t_{1}leqslant {frac {1}{2}}} $0leqslant t_{1}leqslant {frac {1}{2}}$

f∗g(t1,t2,…tn)=g(2t1−1,t2,…tn){displaystyle f*g(t_{1},t_{2},ldots t_{n})=g(2t_{1}-1,t_{2},ldots t_{n})}

$f*g(t_{1},t_{2},ldots t_{n})=g(2t_{1}-1,t_{2},ldots t_{n})$ , если 12⩽t1⩽1{displaystyle {frac {1}{2}}leqslant t_{1}leqslant 1} ${frac {1}{2}}leqslant t_{1}leqslant 1$

Так как на границе куба f=g=x0{displaystyle f=g=x_{0}}

$f=g=x_{0}$ , то умножение определено корректно. Легко проверить, что [f∗g]{displaystyle [f*g]} $[f*g]$ зависит только от гомотопического класса [f]{displaystyle [f]} $[f]$ и [g]{displaystyle [g]} $[g]$ . Это умножение удовлетворяет всем аксиомам группы. В случае n=1{displaystyle n=1} $n=1$ мы имеем общеизвестное умножение замкнутых путей и, следовательно, π1(X,x0){displaystyle pi _{1}(X,x_{0})} $pi _{1}(X,x_{0})$ является фундаментальной группой. При n>1 πn(X,x0){displaystyle pi _{n}(X,x_{0})} $pi _{n}(X,x_{0})$ называются высшими гомотопическими группами.

Непрерывному отображению пространств F:(X,x0)→(Y,y0){displaystyle Fcolon (X,x_{0})to (Y,y_{0})}

$Fcolon (X,x_{0})to (Y,y_{0})$ сооветствует гомоморфизм F∗:πn(X,x0)→πn(Y,y0){displaystyle F_{*}colon pi _{n}(X,x_{0})to pi _{n}(Y,y_{0})} $F_{*}colon pi _{n}(X,x_{0})to pi _{n}(Y,y_{0})$ , причём это соответствие, как говорят, функториально, то есть произведению непрерывных отображений соответствует произведение гомоморфизмов гомотопических групп (FG)∗=F∗G∗{displaystyle (FG)_{*}=F_{*}G_{*}} $(FG)_{*}=F_{*}G_{*}$ , а тождественному
отображению соответствует тождественный гомоморфизм (id)∗=id∗{displaystyle (id)_{*}=id_{*}} $(id)_{*}=id_{*}$ . Если отображение F{displaystyle F} $F$ гомотопно G{displaystyle G} $G$ , то F∗=G∗{displaystyle F_{*}=G_{*}} $F_{*}=G_{*}$ .

Зависимость от начальной точки

В отличие от гомологических групп Hn(X){displaystyle H_{n}(X)}

$H_{n}(X)$ в определение гомотопических групп πn(X,x0){displaystyle pi _{n}(X,x_{0})} $pi _{n}(X,x_{0})$ входит выделенная точка x0{displaystyle x_{0}} $x_{0}$ . На самом деле в случае линейно связных пространств эти группы изоморфны, хотя в общем случае канонического изоморфизма не существует.

Абелевость высших гомотопических групп

В то время как фундаментальная группа π1(X,x0){displaystyle pi _{1}(X,x_{0})}

$pi _{1}(X,x_{0})$ в общем случае неабелева, для всех n>1 πn(X,x0){displaystyle pi _{n}(X,x_{0})} $pi _{n}(X,x_{0})$ абелевы, то есть [f][g]=[g][f]{displaystyle [f][g]=[g][f]} $[f][g]=[g][f]$ . Наглядное доказательство этого факта можно видеть на следующем рисунке (светло-синие области отображаются в точку x0{displaystyle x_{0}} 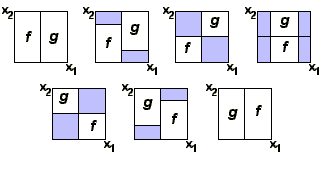$x_{0}$ ):

Относительные гомотопические группы и точная гомотопическая последовательность

Относительные гомотопические группы определяются для пространства X{displaystyle X}

$X$ , его подпространства A⊂X{displaystyle Asubset X} $Asubset X$ и выделенной точки x0∈X{displaystyle x_{0}in X} $x_{0}in X$ . Пусть In⊂Rn{displaystyle I^{n}subset mathbb {R} ^{n}} $I^{n}subset mathbb{R} ^{n}$ — единичный куб (In={(t1,t2,…tn):0⩽tn⩽1}{displaystyle I^{n}={(t_{1},t_{2},ldots t_{n}):0leqslant t_{n}leqslant 1}} ${displaystyle I^{n}={(t_{1},t_{2},ldots t_{n}):0leqslant t_{n}leqslant 1}}$ ), ∂In{displaystyle partial I^{n}} $partial I^{n}$ — граница этого куба, a In−1⊂∂In{displaystyle I^{n-1}subset partial I^{n}} $I^{{n-1}}subset partial I^{n}$ — грань куба, определяемая уравнением xn=0{displaystyle x_{n}=0} ${displaystyle x_{n}=0}$ . Множество гомотопических классов [f]{displaystyle [f]} $[f]$ непрерывных отображений f:In→X{displaystyle fcolon I^{n}to X} $fcolon I^{n}to X$ , для которых f:In−1→A{displaystyle fcolon I^{n-1}to A} $fcolon I^{{n-1}}to A$ и на остальных гранях f:∂In∖Int⁡(In−1)→x0{displaystyle fcolon partial I^{n}setminus operatorname {Int} (I^{n-1})to x_{0}} $fcolon partial I^{n}setminus operatorname {Int}(I^{{n-1}})to x_{0}$ обозначается πn(X,A,x0){displaystyle pi _{n}(X,A,x_{0})} $pi _{n}(X,A,x_{0})$ (причём In−1{displaystyle I^{n-1}} $I^{{n-1}}$ переходит в A{displaystyle A} $A$ , а ∂In∖Int⁡(In−1){displaystyle partial I^{n}setminus operatorname {Int} (I^{n-1})} $partial I^{n}setminus operatorname {Int}(I^{{n-1}})$ в точку x0{displaystyle x_{0}} $x_{0}$ при всех отображениях и гомотопиях).

Точно так же, как и раньше можно доказать что при n⩾2{displaystyle ngeqslant 2}

$ngeqslant 2$ это множество образует группу — относительную гомотопическую группу порядка n{displaystyle n} $n$ . Если n⩾3{displaystyle ngeqslant 3} $ngeqslant 3$ то предыдущий рисунок доказывает, что πn(X,A,x0){displaystyle pi _{n}(X,A,x_{0})} $pi _{n}(X,A,x_{0})$ — абелева. (При n=2 доказательство не проходит, так как точки I1={x:x2=0}{displaystyle I^{1}={x:x_{2}=0}} $I^{1}={x:x_{2}=0}$ могут переходить в точки A{displaystyle A} $A$ , отличные от x0{displaystyle x_{0}} $x_{0}$ ).

Вложение i:(A,x0)→(X,x0){displaystyle icolon (A,x_{0})to (X,x_{0})}

$icolon (A,x_{0})to (X,x_{0})$ индуцирует гомоморфизм i∗:πn(A,x0→πn(X,x0){displaystyle i_{*}colon pi _{n}(A,x_{0}to pi _{n}(X,x_{0})} ${displaystyle i_{*}colon pi _{n}(A,x_{0}to pi _{n}(X,x_{0})}$ , а вложение j:(X,x0)→(X,A,x0){displaystyle jcolon (X,x_{0})to (X,A,x_{0})} $jcolon (X,x_{0})to (X,A,x_{0})$ (здесь (X,x0){displaystyle (X,x_{0})} $(X,x_{0})$ следует понимать как (X,x0,x0){displaystyle (
X,x_{0},x_{0})} $(X,x_{0},x_{0})$ ), индуцирует гомоморфизм j∗:πn(X,x0)→πn(X,A,x0){displaystyle j_{*}colon pi _{n}(X,x_{0})to pi _{n}(X,A,x_{0})} $j_{*}colon pi _{n}(X,x_{0})to pi _{n}(X,A,x_{0})$ . Любой элемент [f]∈πn(X,A,x0){displaystyle [f]in pi _{n}(X,A,x_{0})} $[f]in pi _{n}(X,A,x_{0})$ определяется отображением f{displaystyle f} $f$ , которое, в частности, переводит In−1{displaystyle I^{n-1}} $I^{{n-1}}$ в A{displaystyle A} $A$ , причём на ∂In−1{displaystyle partial I^{n-1}} $partial I^{{n-1}}$ f тождественно равно x0{displaystyle x_{0}} $x_{0}$ , определяя элемент из πn−1(A,x0){displaystyle pi _{n-1}(A,x_{0})} $pi _{{n-1}}(A,x_{0})$ . Таким образом мы получаем отображение ∂πn(X,A,x0)→πn−1(A,x0){displaystyle partial pi _{n}(X,A,x_{0})to pi _{n-1}(A,x_{0})} $partial pi _{n}(X,A,x_{0})to pi _{{n-1}}(A,x_{0})$ , которое является гомоморфизмом. Мы имеем следующую последовательность групп и гомоморфизмов:
…⟶πn(A,x0)⟶i∗nπn(X,x0)⟶j∗nπn(X,A,x0)⟶∂nπn−1(A,x0)⟶ …{displaystyle …{longrightarrow }pi _{n}(A,x_{0}){stackrel {i_{*n}}{longrightarrow }}pi _{n}(X,x_{0}){stackrel {j_{*n}}{longrightarrow }}pi _{n}(X,A,x_{0}){stackrel {partial _{n}}{longrightarrow }}pi _{n-1}(A,x_{0}){longrightarrow }~…} $...{longrightarrow }pi _{n}(A,x_{0}){stackrel {i_{{*n}}}{longrightarrow }}pi _{n}(X,x_{0}){stackrel {j_{{*n}}}{longrightarrow }}pi _{n}(X,A,x_{0}){stackrel {partial _{n}}{longrightarrow }}pi _{{n-1}}(A,x_{0}){longrightarrow }~...$

Эта последовательность является точной, то есть образ любого гомоморфизма совпадает с ядром следующего гомоморфизма. Отсюда в случае, когда πn(X,x0)=0{displaystyle pi _{n}(X,x_{0})=0}

$pi _{n}(X,x_{0})=0$ для всех n⩾1{displaystyle ngeqslant 1} $ngeqslant 1$ , граничный гомоморфизм ∂:πn+1(X,A,x0)→πn(A,x0){displaystyle partial colon pi _{n+1}(X,A,x_{0})to pi _{n}(A,x_{0})} $partial colon pi _{{n+1}}(X,A,x_{0})to pi _{n}(A,x_{0})$ будет изоморфизмом.

История

Фундаментальная группа была введена создателем топологии А. Пуанкаре, высшие гомотопические группы — В. Гуревичем. Несмотря на простоту их определения, вычисление конкретных групп (даже для таких простых пространств, как сферы Sn) часто является очень трудной задачей, причём более-менее общие методы были получены только начиная с середины XX века.

См. также

Убивающие пространства

Литература

Дубровин Б. А., Новиков С. П., Фоменко А. Т. Современная геометрия: Методы и приложения. — М.: Наука, 1979
Рохлин В. А., Фукс Д. Б. Начальный курс топологии. Геометрические главы. — М.: Наука, 1977
Свитцер Р. М. Алгебраическая топологи
я — гомотопии и гомологии. — М.: Наука, 1985
Спеньер Э. Алгебраическая топология. — М.: Мир, 1971
Фоменко А. Т., Фукс Д. Б. Курс гомотопической топологии. — М.: Наука, 1989