Тригонометрические функции

Разделы:

Запросы «sin» и «синус» перенаправляются сюда; у терминов sin и синус есть также другие значения.Запрос «sec» перенаправляется сюда; см. также другие значения.О функциях, выражающихся через экспоненту см. гиперболические функции.

Тригонометри́ческие фу́нкции — элементарные функции [1], которые исторически возникли при рассмотрении прямоугольных треугольников и выражали зависимости длин сторон этих треугольников от острых углов при гипотенузе (или, что равнозначно, зависимость хорд и высот от центрального угла дуги в круге). Эти функции нашли широкое применение в самых разных областях науки. По мере развития математики определение тригонометрических функций было расширено, в современном понимании их аргументом может быть произвольное вещественное или комплексное число.

Рис. 1.
Графики тригонометрических функций: синуса, косинуса, тангенса, котангенса, секанса, косеканса

Раздел математики, изучающий свойства тригонометрических функций, называется тригонометрией.

К тригонометрическим функциям традиционно причисляют:

прямые тригонометрические функции:

синус (sin⁡x{displaystyle sin x} $sin x$ );
косинус (cos⁡x{displaystyle cos x} $cos x$ );

производные тригонометрические функции:

тангенс (tgx=sin⁡xcos⁡x){displaystyle left(mathrm {tg} ,x={frac {sin x}{cos x}}right)} ${displaystyle left(mathrm {tg} ,x={frac {sin x}{cos x}}right)}$ ;
котангенс (ctgx=cos⁡xsin⁡x){displaystyle left(mathrm {ctg} ,x={frac {cos x}{sin x}}right)} ${displaystyle left(mathrm {ctg} ,x={frac {cos x}{sin x}}right)}$ ;

секанс (sec⁡x=1cos⁡x){displaystyle left(sec x={frac {1}{cos x}}right)} ${displaystyle left(sec x={frac {1}{cos x}}right)}$ ;
косеканс (cosecx=1sin⁡x){displaystyle left(mathrm {cosec} ,x={frac {1}{sin x}}right)} ${displaystyle left(mathrm {cosec} ,x={frac {1}{sin x}}right)}$ ;

обратные тригонометрические функции:

арксинус, арккосинус и т. д.

В типографике литературы на разных языках сокращённое обозначение тригонометрических функций различно, например, в англоязычной литературе тангенс, котангенс и косеканс обозначаются tan⁡x{displaystyle tan x} ${displaystyle tan x}$ , cot⁡x{displaystyle cot x} ${displaystyle cot x}$ , csc⁡x{displaystyle csc x} $csc x$ . До Второй мировой войны в Германии и во Франции эти функции обозначались так же, как принято в русскоязычных текстах[2], но потом в литературе на языках этих стран был принят англоязычный вариант записи тригонометрических функций.

Кроме этих шести широко известных тригонометрических функций, иногда в литературе используются некоторые редко используемые тригонометрические функции (версинус и т. д.).

Синус и косинус вещественного аргумента представляют собой периодические, непрерывные и бесконечно дифференцируемые вещественнозначные функции. Остальные четыре функции на вещественной оси также вещественнозначны, периодичны и бесконечно дифференцируемы, за исключением счётного числа разрывов второго рода: у тангенса и секанса в точках ±πn+π2{displaystyle pm pi n+{frac {pi }{2}}} $pm pi n + frac{pi}{2}$ , а у котангенса и косеканса — в точках ±πn{displaystyle pm pi n} $pm pi n$ .
Графики тригонометрических функций показаны на рис. 1.

Содержание

1 Способы определения
2 Значения тригонометрических функций для некоторых углов
- 2.1 Значения тригонометрических функций нестандартных углов
3 Свойства тригонометрических функций
4 Исследование функций в математическом анализе
5 Тригонометрические функции комплексного аргумента
- 5.1 Определение
- 5.2 Комплексные графики
6 История названий
7 См. также
8 Литература
9 Ссылки
10 Примечания

Способы определения

Определение для острых углов

Рис. 4.
Тригонометрические функции острого угла

В геометрии тригонометрические функции острого угла определяются отношениями сторон прямоугольного треугольника [3]. Пусть △AOB{displaystyle triangle AOB}

${displaystyle triangle AOB}$ — прямоугольный, с острым углом ∠AOB=α{displaystyle angle AOB=alpha } ${displaystyle angle AOB=alpha }$ и гипотенузой OB{displaystyle OB} $OB$ . Тогда:

sin⁡α=ABOB{displaystyle sin alpha ={frac {AB}{OB}}} ${displaystyle sin alpha ={frac {AB}{OB}}}$ (синусом угла α{displaystyle alpha } $alpha$ называется отношение противолежащего катета к гипотенузе);
cos⁡α=OAOB{displaystyle cos alpha ={frac {OA}{OB}}} ${displaystyle cos alpha ={frac {OA}{OB}}}$ (косинусом угла α{displaystyle alpha } $alpha$ называется отношение прилежащего катета к гипотенузе);
tgα=ABOA{displaystyle mathrm {tg} ,alpha ={frac {AB}{OA}}} ${displaystyle mathrm {tg} ,alpha ={frac {AB}{OA}}}$ (тангенсом угла α{displaystyle alpha } $alpha$ называется отношение противолежащего катета к прилежащему);
ctgα=OAAB{displaystyle mathrm {ctg} ,alpha ={frac {OA}{AB}}} ${displaystyle mathrm {ctg} ,alpha ={frac {OA}{AB}}}$ (котангенсом угла α{displaystyle alpha } $alpha$ называется отношение прилежащего катета к противолежащему);
secα=OBOA{displaystyle mathrm {sec} ,alpha ={frac {OB}{OA}}} ${displaystyle mathrm {sec} ,alpha ={frac {OB}{OA}}}$ (секансом угла α{displaystyle alpha } $alpha$ называется отношение гипотенузы к прилежащему катету);
cosecα=OBAB{displaystyle mathrm {cosec} ,alpha ={frac {OB}{AB}}} ${displaystyle mathrm {cosec} ,alpha ={frac {OB}{AB}}}$ (косекансом угла α{displaystyle alpha } $alpha$ называется отношение гипотенузы к противолежащему катету).

Данное определение имеет некоторое методическое преимущество, так как не требует введения понятия системы координат, но также и такой крупный недостаток, что невозможно определить тригонометрические функции даже для тупых углов, которые необходимо знать при решении элементарных задач о тупоугольных треугольниках. (См.: теорема синусов, теорема косинусов).

Определение для любых углов

Рис. 2.
Определение тригонометрических функций

Обычно тригонометрические функции определяются геометрически [4]. В декартовой системе координат на плоскости построим окружность единичного радиуса (R=1{displaystyle R=1}

$R=1$ ) с центром в начале координат O{displaystyle O} $O$ . Всякий угол станем рассматривать как поворот от положительного направления оси абсцисс до некоторого луча OB{displaystyle OB} $OB$ (точку B{displaystyle B} $B$ выбираем на окружности), при этом направление поворота против часовой стрелки считаем положительным, а по часовой стрелке — отрицательным. Абсциссу точки B{displaystyle B} $B$ обозначим xB{displaystyle x_{B}} $x_B$ , а ординату — yB{displaystyle y_{B}} $y_B$ (см. рисунок 2).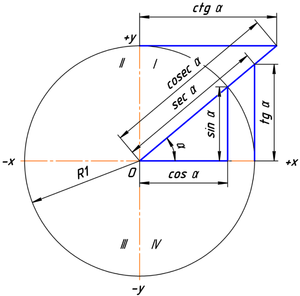 Рис. 3.
Численные значения тригонометрических функций угла α{displaystyle alpha } $alpha$ в тригонометрической окружности с радиусом, равным единице

Определим функции следующим образом:

sin⁡α=yB{displaystyle sin alpha =y_{B}} ${displaystyle sin alpha =y_{B}}$ , cos⁡α=xB{displaystyle cos alpha =x_{B}} ${displaystyle cos alpha =x_{B}}$ ;
tg⁡α=yBxB{displaystyle operatorname {tg} alpha ={frac {y_{B}}{x_{B}}}} ${displaystyle operatorname {tg} alpha ={frac {y_{B}}{x_{B}}}}$ , ctg⁡α=xByB{displaystyle operatorname {ctg} alpha ={frac {x_{B}}{y_{B}}}} ${displaystyle operatorname {ctg} alpha ={frac {x_{B}}{y_{B}}}}$ ;
sec⁡α=1xB{displaystyle sec alpha ={frac {1}{x_{B}}}} ${displaystyle sec alpha ={frac {1}{x_{B}}}}$ , cosec⁡α=1yB{displaystyle operatorname {cosec} alpha ={frac {1}{y_{B}}}} ${displaystyle operatorname {cosec} alpha ={frac {1}{y_{B}}}}$ .

Нетрудно видеть, что такое определение так же основывается на отношениях прямоугольного треугольника, с тем отличием, что учитывается знак (±1{displaystyle pm 1}

$pm 1$ ). Поэтому тригонометрические функции можно определить и по окружности произвольного радиуса R{displaystyle R} $R$ , однако формулы придётся нормировать. На рисунке 3 показаны величины тригонометрических функций для единичной окружности.

В тригонометрии удобным оказывается вести счёт углов не в градусной мере, а в радианной. Так, угол в 360∘{displaystyle 360^{circ }}

${displaystyle 360^{circ }}$ запишется длиной единичной окружности 2π{displaystyle 2pi } $2pi$ . Угол в 180∘{displaystyle 180^{circ }} $180^{circ }$ равен, соответственно π{displaystyle pi } $pi$ и так далее. Заметим, что угол на 2π{displaystyle 2pi } $2pi$ отличающийся от α{displaystyle alpha } $alpha$ по рисунку эквивалентен α{displaystyle alpha } $alpha$ , вследствие чего заключим, что тригонометрические функции периодичны.

Наконец, определим тригонометрические функции вещественного числа x{displaystyle x}

$x$ тригонометрическими функциями угла, радианная мера которого равна x{displaystyle x} $x$ .

Определение как решений дифференциальных уравнений

Синус и косинус можно определить как единственные функции, вторые производные которых равны самим функциям, взятым со знаком минус:

(cos⁡x)″=−cos⁡x,{displaystyle left(cos xright)»=-cos x,}

left(cos xright)'' = - cos x,

(sin⁡x)″=−sin⁡x.{displaystyle left(sin xright)»=-sin x.}

left(sin xright)'' = - sin x.

То есть задать их как чётное (косинус) и нечётное (синус) решения дифференциального уравнения

d2dφ2R(φ)=−R(φ),{displaystyle {frac {d^{2}}{dvarphi ^{2}}}R(varphi )=-R(varphi ),}

frac{d^2}{dvarphi^2}R(varphi) = - R(varphi),

с дополнительными условиями:R(0)=1{displaystyle R(0)=1}

$R(0)=1$ для косинуса и R′(0)=1{displaystyle R'(0)=1} $R'(0)=1$ для синуса.

Определение как решений функциональных уравнений

Функции косинус и синус можно определить[5]как решения (f{displaystyle f}

$f$ и g{displaystyle g} $g$ соответственно) системы функциональных уравнений:

{f(x+y)=f(x)f(y)−g(x)g(y)g(x+y)=g(x)f(y)+f(x)g(y){displaystyle left{{begin{array}{rcl}f(x+y)&=&f(x)f(y)-g(x)g(y)\g(x+y)&=&g(x)f(y)+f(x)g(y)end{array}}right.}

$left{ begin{array}{rcl} f(x+y)&=&f(x)f(y)-g(x)g(y)\ g(x+y)&=&g(x)f(y)+f(x)g(y) end{array} right.$

при дополнительных условиях:

f(x)2+g(x)2=1,{displaystyle f(x)^{2}+g(x)^{2}=1,}

$f(x)^{2}+g(x)^{2}=1,$ g(π/2)=1,{displaystyle g(pi /2)=1,} $g(pi /2)=1,$ и 0<g(x)<1{displaystyle 0<g(x)<1} ${displaystyle 0<g(x)<1}$ при 0<x<π/2{displaystyle 0<x<pi /2} $0<x<pi /2$ .

Определение через ряды

Используя геометрию и свойства пределов, можно доказать, что производная синуса равна косинусу, и что производная косинуса равна минус синусу. Тогда можно воспользоваться теорией рядов Те
йлора и представить синус и косинус в виде степенны́х рядов:

sin⁡x=x−x33!+x55!−x77!+x99!−⋯=∑n=0∞(−1)nx2n+1(2n+1)!,{displaystyle sin x=x-{frac {x^{3}}{3!}}+{frac {x^{5}}{5!}}-{frac {x^{7}}{7!}}+{frac {x^{9}}{9!}}-cdots =sum _{n=0}^{infty }{frac {(-1)^{n}x^{2n+1}}{(2n+1)!}},}

sin x=x-frac{x^3}{3!}+frac{x^5}{5!}-frac{x^7}{7!}+frac{x^9}{9!}-cdots = sum_{n=0}^inftyfrac{(-1)^nx^{2n+1}}{(2n+1)!},

cos⁡x=1−x22!+x44!−x66!+x88!−⋯=∑n=0∞(−1)nx2n(2n)!.{displaystyle cos x=1-{frac {x^{2}}{2!}}+{frac {x^{4}}{4!}}-{frac {x^{6}}{6!}}+{frac {x^{8}}{8!}}-cdots =sum _{n=0}^{infty }{frac {(-1)^{n}x^{2n}}{(2n)!}}.}

cos x=1-frac{x^2}{2!}+frac{x^4}{4!}-frac{x^6}{6!}+frac{x^8}{8!}-cdots = sum_{n=0}^inftyfrac{(-1)^nx^{2n}}{(2n)!}.

Пользуясь этими формулами, а также равенствами tgx=sin⁡xcos⁡x,{displaystyle operatorname {tg} ,x={frac {sin x}{cos x}},}

$operatorname{tg},x=frac{sin x}{cos x},$ ctgx=cos⁡xsin⁡x,{displaystyle operatorname {ctg} ,x={frac {cos x}{sin x}},} $operatorname{ctg},x=frac{cos x}{sin x},$ sec⁡x=1cos⁡x{displaystyle sec x={frac {1}{cos x}}} $sec x=frac{1}{cos x}$ и cosecx=1sin⁡x,{displaystyle operatorname {cosec} ,x={frac {1}{sin x}},} $operatorname{cosec},x=frac{1}{sin x},$ можно найти разложения в ряд и других тригонометрических функций:

tgx=x+13×3+215×5+17315×7+622835×9+⋯=∑n=1∞22n(22n−1)|B2n|(2n)!x2n−1(−π2<x<π2),{displaystyle {operatorname {tg} ,x=x+{frac {1}{3}},x^{3}+{frac {2}{15}},x^{5}+{frac {17}{315}},x^{7}+{frac {62}{2835}},x^{9}+cdots =sum _{n=1}^{infty }{frac {2^{2n}(2^{2n}-1)|B_{2n}|}{(2n)!}}x^{2n-1}quad left(-{frac {pi }{2}}<x<{frac {pi }{2}}right),}}

{operatorname{tg},x=x+frac{1}{3},x^3 + frac{2}{15},x^5 + frac{17}{315},x^7 + frac{62}{2835},x^9 + cdots = sum_{n=1}^inftyfrac{2^{2n}(2^{2n}-1)|B_{2n}|}{(2n)!}x^{2n-1} quad left(-frac{pi}{2}<x<frac{pi}{2}right),}

ctgx=1x−x3−x345−2×5945−x74725−⋯=1x−∑n=1∞22n|B2n|(2n)!x2n−1(−π<x<π),{displaystyle {operatorname {ctg} ,x={frac {1}{x}}-{frac {x}{3}}-{frac {x^{3}}{45}}-{frac {2x^{5}}{945}}-{frac {x^{7}}{4725}}-cdots ={frac {1}{x}}-sum _{n=1}^{infty }{frac {2^{2n}|B_{2n}|}{(2n)!}},x^{2n-1}quad left(-pi <x<pi right),}}

{operatorname{ctg},x = frac{1}{x} - frac{x}{3} - frac{x^3}{45} - frac{2x^5}{945} - frac{x^7}{4725} - cdots = frac{1}{x} - sum_{n=1}^infty frac{2^{2n}|B_{2n}|}{(2n)!},x^{2n-1} quad left(-pi < x < piright),}

sec⁡x=1+12×2+524×4+61720×6+2778064×8+⋯=∑n=0∞|En|(2n)!x2n,(−π2<x<π2),{displaystyle {sec x=1+{frac {1}{2}},x^{2}+{frac {5}{24}},x^{4}+{frac {61}{720}},x^{6}+{frac {277}{8064}},x^{8}+cdots =sum _{n=0}^{infty }{frac {|E_{n}|}{(2n)!}},x^{2n},quad left(-{frac {pi }{2}}<x<{frac {pi }{2}}right),}}

{sec x=1+frac{1}{2},x^2+frac{5}{24},x^4+frac{61}{720},x^6+frac{277}{8064},x^8+cdots = sum_{n=0}^inftyfrac{|E_{n}|}{(2n)!},x^{2n}, quad left(-frac{pi}{2} < x < frac{pi}{2}right),}

cosec⁡x=1x+16x+7360×3+3115120×5+127604800×7+⋯=1x+∑n=1∞2(22n−1−1)|B2n|(2n)!x2n−1(−π<x<π),{displaystyle operatorname {cosec} x={frac {1}{x}}+{frac {1}{6}},x+{frac {7}{360}},x^{3}+{frac {31}{15120}},x^{5}+{frac {127}{604800}},x^{7}+cdots ={frac {1}{x}}+sum _{n=1}^{infty }{frac {2(2^{2n-1}-1)|B_{2n}|}{(2n)!}},x^{2n-1}quad left(-pi <x<pi right),}

operatorname{cosec} x = frac{1}{x} + frac{1}{6},x + frac{7}{360},x^3 + frac{31}{15120},x^5 + frac{127}{604800},x^7 + cdots = frac{1}{x} + sum_{n=1}^infty frac{2(2^{2n-1}-1) |B_{2n}|}{(2n)!},x^{2n-1} quad left(-pi < x < piright),

где

Bn{displaystyle B_{n}}

B_{n}

— числа Бернулли,

En{displaystyle E_{n}}

E_{n}

— числа Эйлера.

Значения тригонометрических функций для некоторых углов

Основная статья: Тригонометрические константы

Значения синуса, косинуса, тангенса, котангенса, секанса и косеканса для некоторых углов приведены в таблице. («∞{displaystyle infty }

$infty$ » означает, что функция в указанной точке не определена, а в её окрестности стремится к бесконечности).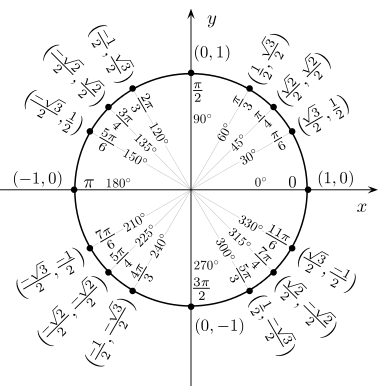 Значения косинуса и синуса на окружности

Радианы	0{displaystyle 0} ${displaystyle 0}$	π6{displaystyle {frac {pi }{6}}} ${displaystyle {frac {pi }{6}}}$	π4{displaystyle {frac {pi }{4}}} ${displaystyle {frac {pi }{4}}}$	π3{displaystyle {frac {pi }{3}}} ${displaystyle {frac {pi }{3}}}$	π2{displaystyle {frac {pi }{2}}} ${displaystyle {frac {pi }{2}}}$	π{displaystyle pi } $pi$	3π2{displaystyle {frac {3pi }{2}}} ${displaystyle {frac {3pi }{2}}}$	2π{displaystyle 2pi } $2pi$
Градусы	0∘{displaystyle 0^{circ }} ${displaystyle 0^{circ }}$	30∘{displaystyle 30^{circ }} ${displaystyle 30^{circ }}$	45∘{displaystyle 45^{circ }} ${displaystyle 45^{circ }}$	60∘{displaystyle 60^{circ }} ${displaystyle 60^{circ }}$	90∘{displaystyle 90^{circ }} ${displaystyle 90^{circ }}$	180∘{displaystyle 180^{circ }} ${displaystyle 180^{circ }}$	270∘{displaystyle 270^{circ }} ${displaystyle 270^{circ }}$	360∘{displaystyle 360^{circ }} ${displaystyle 360^{circ }}$
sin⁡α{displaystyle sin alpha } ${displaystyle sin alpha }$	0{displaystyle 0} ${displaystyle 0}$	12{displaystyle {frac {1}{2}}} ${frac {1}{2}}$	22{displaystyle {frac {sqrt {2}}{2}}} $frac{sqrt{2}}{2}$	32{displaystyle {frac {sqrt {3}}{2}}} $frac{sqrt{3}}{2}$	1{displaystyle 1} $1$	0{displaystyle 0} ${displaystyle 0}$	−1{displaystyle -1} $-1$	0{displaystyle 0} ${displaystyle 0}$
cos⁡α{displaystyle cos alpha } $cos alpha$	1{displaystyle 1} $1$	32{displaystyle {frac {sqrt {3}}{2}}} $frac{sqrt{3}}{2}$	22{displaystyle {frac {sqrt {2}}{2}}} $frac{sqrt{2}}{2}$	12{displaystyle {frac {1}{2}}} ${frac {1}{2}}$	0{displaystyle 0} ${displaystyle 0}$	−1{displaystyle -1} $-1$	0{displaystyle 0} ${displaystyle 0}$	1{displaystyle 1} $1$
tgα{displaystyle operatorname {tg} ,alpha } $operatorname{tg},alpha$	0{displaystyle 0} ${displaystyle 0}$	13{displaystyle {frac {1}{sqrt {3}}}} ${displaystyle {frac {1}{sqrt {3}}}}$	1{displaystyle 1} $1$	3{displaystyle {sqrt {3}}} $sqrt{3}$	∞{displaystyle infty } $infty$	0{displaystyle 0} ${displaystyle 0}$	∞{displaystyle infty } $infty$	0{displaystyle 0} ${displaystyle 0}$
ctgα{displaystyle operatorname {ctg} ,alpha } $operatorname{ctg},alpha$	∞{displaystyle infty } $infty$	3{displaystyle {sqrt {3}}} $sqrt{3}$	1{displaystyle 1} $1$	33{displaystyle {frac {sqrt {3}}{3}}} $frac{sqrt{3}}{3}$	0{displaystyle 0} ${displaystyle 0}$	∞{displaystyle infty } $infty$	0{displaystyle 0} ${displaystyle 0}$	∞{displaystyle infty } $infty$
sec⁡α{displaystyle sec alpha } ${displaystyle sec alpha }$	1{displaystyle 1} $1$	233{displaystyle {frac {2{sqrt {3}}}{3}}} ${displaystyle {frac {2{sqrt {3}}}{3}}}$	2{displaystyle {sqrt {2}}} ${sqrt {2}}$	2{displaystyle 2} $2$	∞{displaystyle infty } $infty$	−1{displaystyle -1} $-1$	∞{displaystyle infty } $infty$	1{displaystyle 1} $1$
cosecα{displaystyle operatorname {cosec} ,alpha } ${displaystyle operatorname {cosec} ,alpha }$	∞{displaystyle infty } $infty$	2{displaystyle 2} $2$	2{displaystyle {sqrt {2}}} ${sqrt {2}}$	233{displaystyle {frac {2{sqrt {3}}}{3}}} ${displaystyle {frac {2{sqrt {3}}}{3}}}$	1{displaystyle 1} $1$	∞{displaystyle infty } $infty$	−1{displaystyle -1} $-1$	∞{displaystyle infty } $infty$

Значения тригонометрических функций нестандартных углов

Радианы	2π3{displaystyle {frac {2pi }{3}}} ${displaystyle {frac {2pi }{3}}}$	3π4{displaystyle {frac {3pi }{4}}} ${displaystyle {frac {3pi }{4}}}$	5π6{displaystyle {frac {5pi }{6}}} ${displaystyle {frac {5pi }{6}}}$	7π6{displaystyle {frac {7pi }{6}}} ${displaystyle {frac {7pi }{6}}}$	5π4{displaystyle {frac {5pi }{4}}} ${displaystyle {frac {5pi }{4}}}$	4π3{displaystyle {frac {4pi }{3}}} ${displaystyle {frac {4pi }{3}}}$	5π3{displaystyle {frac {5pi }{3}}} ${displaystyle {frac {5pi }{3}}}$	7π4{displaystyle {frac {7pi }{4}}} ${displaystyle {frac {7pi }{4}}}$	11π6{displaystyle {frac {11pi }{6}}} ${displaystyle {frac {11pi }{6}}}$
Градусы	120∘{displaystyle 120^{circ }} ${displaystyle 120^{circ }}$	135∘{displaystyle 135^{circ }} ${displaystyle 135^{circ }}$	150∘{displaystyle 150^{circ }} ${displaystyle 150^{circ }}$	210∘{displaystyle 210^{circ }} ${displaystyle 210^{circ }}$	225∘{displaystyle 225^{circ }} ${displaystyle 225^{circ }}$	240∘{displaystyle 240^{circ }} ${displaystyle 240^{circ }}$	300∘{displaystyle 300^{circ }} ${displaystyle 300^{circ }}$	315∘{displaystyle 315^{circ }} ${displaystyle 315^{circ }}$	330∘{displaystyle 330^{circ }} ${displaystyle 330^{circ }}$
sin⁡α{displaystyle sin alpha } ${displaystyle sin alpha }$	32{displaystyle {frac {sqrt {3}}{2}}} $frac{sqrt{3}}{2}$	22{displaystyle {frac {sqrt {2}}{2}}} $frac{sqrt{2}}{2}$	12{displaystyle {frac {1}{2}}} ${frac {1}{2}}$	−12{displaystyle -{frac {1}{2}}} $-frac{1}{2}$	−22{displaystyle -{frac {sqrt {2}}{2}}} $-frac{sqrt{2}}{2}$	−32{displaystyle -{frac {sqrt {3}}{2}}} $-frac{sqrt{3}}{2}$	−32{displaystyle -{frac {sqrt {3}}{2}}} $-frac{sqrt{3}}{2}$	−22{displaystyle -{frac {sqrt {2}}{2}}} $-frac{sqrt{2}}{2}$	−12{displaystyle -{frac {1}{2}}} $-frac{1}{2}$
cos⁡α{displaystyle cos alpha } $cos alpha$	−12{displaystyle -{frac {1}{2}}} $-frac{1}{2}$	−22{displaystyle -{frac {sqrt {2}}{2}}} $-frac{sqrt{2}}{2}$	−32{displaystyle -{frac {sqrt {3}}{2}}} $-frac{sqrt{3}}{2}$	−32{displaystyle -{frac {sqrt {3}}{2}}} $-frac{sqrt{3}}{2}$	−22{displaystyle -{frac {sqrt {2}}{2}}} $-frac{sqrt{2}}{2}$	−12{displaystyle -{frac {1}{2}}} $-frac{1}{2}$	12{displaystyle {frac {1}{2}}} ${frac {1}{2}}$	22{displaystyle {frac {sqrt {2}}{2}}} $frac{sqrt{2}}{2}$	32{displaystyle {frac {sqrt {3}}{2}}} $frac{sqrt{3}}{2}$
tgα{displaystyle operatorname {tg} ,alpha } $operatorname{tg},alpha$	−3{displaystyle -{sqrt {3}}} $-sqrt{3}$	−1{displaystyle -1} $-1$	−33{displaystyle -{frac {sqrt {3}}{3}}} $-frac{sqrt{3}}{3}$	33{displaystyle {frac {sqrt {3}}{3}}} $frac{sqrt{3}}{3}$	1{displaystyle 1} $1$	3{displaystyle {sqrt {3}}} $sqrt{3}$	−3{displaystyle -{sqrt {3}}} $-sqrt{3}$	−1{displaystyle -1} $-1$	−33{displaystyle -{frac {sqrt {3}}{3}}} $-frac{sqrt{3}}{3}$
ctgα{displaystyle operatorname {ctg} ,alpha } $operatorname{ctg},alpha$	−33{displaystyle -{frac {sqrt {3}}{3}}} $-frac{sqrt{3}}{3}$	−1{displaystyle -1} $-1$	−3{displaystyle -{sqrt {3}}} $-sqrt{3}$	3{displaystyle {sqrt {3}}} $sqrt{3}$	1{displaystyle 1} $1$	33{displaystyle {frac {sqrt {3}}{3}}} $frac{sqrt{3}}{3}$	−33{displaystyle -{frac {sqrt {3}}{3}}} $-frac{sqrt{3}}{3}$	−1{displaystyle -1} $-1$	−3{displaystyle -{sqrt {3}}} $-sqrt{3}$
sec⁡α{displaystyle sec alpha } ${displaystyle sec alpha }$	−2{displaystyle -2} $-2$	−2{displaystyle -{sqrt {2}}} ${displaystyle -{sqrt {2}}}$	−233{displaystyle -{frac {2{sqrt {3}}}{3}}} ${displaystyle -{frac {2{sqrt {3}}}{3}}}$	−233{displaystyle -{frac {2{sqrt {3}}}{3}}} ${displaystyle -{frac {2{sqrt {3}}}{3}}}$	−2{displaystyle -{sqrt {2}}} ${displaystyle -{sqrt {2}}}$	−2{displaystyle -2} $-2$	2{displaystyle 2} $2$	2{displaystyle {sqrt {2}}} ${sqrt {2}}$	233{displaystyle {frac {2{sqrt {3}}}{3}}} ${displaystyle {frac {2{sqrt {3}}}{3}}}$
cosecα{displaystyle operatorname {cosec} ,alpha } ${displaystyle operatorname {cosec} ,alpha }$	233{displaystyle {frac {2{sqrt {3}}}{3}}} ${displaystyle {frac {2{sqrt {3}}}{3}}}$	2{displaystyle {sqrt {2}}} ${sqrt {2}}$	2{displaystyle 2} $2$	−2{displaystyle -2} $-2$	−2{displaystyle -{sqrt {2}}} ${displaystyle -{sqrt {2}}}$	−233{displaystyle -{frac {2{sqrt {3}}}{3}}} ${displaystyle -{frac {2{sqrt {3}}}{3}}}$	−233{displaystyle -{frac {2{sqrt {3}}}{3}}} ${displaystyle -{frac {2{sqrt {3}}}{3}}}$	−2{displaystyle -{sqrt {2}}} ${displaystyle -{sqrt {2}}}$	−2{displaystyle -2} $-2$

Радианы	π12{displaystyle {frac {pi }{12}}} ${displaystyle {frac {pi }{12}}}$	π10{displaystyle {frac {pi }{10}}} ${displaystyle {frac {pi }{10}}}$	π8{displaystyle {frac {pi }{8}}} ${displaystyle {frac {pi }{8}}}$	π5{displaystyle {frac {pi }{5}}} ${displaystyle {frac {pi }{5}}}$	3π10{displaystyle {frac {3pi }{10}}} ${displaystyle {frac {3pi }{10}}}$	3π8{displaystyle {frac {3pi }{8}}} ${displaystyle {frac {3pi }{8}}}$	2π5{displaystyle {frac {2pi }{5}}} ${displaystyle {frac {2pi }{5}}}$	5π12{displaystyle {frac {5pi }{12}}} ${displaystyle {frac {5pi }{12}}}$
Градусы	15∘{displaystyle 15^{circ }} ${displaystyle 15^{circ }}$	18∘{displaystyle 18^{circ }} ${displaystyle 18^{circ }}$	22,5∘{displaystyle 22{,}5^{circ }} ${ displaystyle 22{,}5^{circ }}$	36∘{displaystyle 36^{circ }} ${displaystyle 36^{circ }}$	54∘{displaystyle 54^{circ }} ${displaystyle 54^{circ }}$	67,5∘{displaystyle 67{,}5^{circ }} ${displaystyle 67{,}5^{circ }}$	72∘{displaystyle 72^{circ }} ${displaystyle 72^{circ }}$	75∘{displaystyle 75^{circ }} ${displaystyle 75^{circ }}$
sin⁡α{displaystyle sin alpha } ${displaystyle sin alpha }$	2−32{displaystyle {frac {sqrt {2-{sqrt {3}}}}{2}}} ${displaystyle {frac {sqrt {2-{sqrt {3}}}}{2}}}$	5−14{displaystyle {frac {{sqrt {5}}-1}{4}}} $frac{sqrt{5}-1}{4}$	2−22{displaystyle {frac {sqrt {2-{sqrt {2}}}}{2}}} $frac{sqrt{2-sqrt{2}}}{2}$	10−254{displaystyle {frac {sqrt {10-2{sqrt {5}}}}{4}}} ${displaystyle {frac {sqrt {10-2{sqrt {5}}}}{4}}}$	5+14{displaystyle {frac {{sqrt {5}}+1}{4}}} $frac{sqrt{5}+1}{4}$	2+22{displaystyle {frac {sqrt {2+{sqrt {2}}}}{2}}} $frac{sqrt{2+sqrt{2}}}{2}$	10+254{displaystyle {frac {sqrt {10+2{sqrt {5}}}}{4}}} ${displaystyle {frac {sqrt {10+2{sqrt {5}}}}{4}}}$	2+32{displaystyle {frac {sqrt {2+{sqrt {3}}}}{2}}} ${displaystyle {frac {sqrt {2+{sqrt {3}}}}{2}}}$
cos⁡α{displaystyle cos alpha } $cos alpha$	2+32{displaystyle {frac {sqrt {2+{sqrt {3}}}}{2}}} ${displaystyle {frac {sqrt {2+{sqrt {3}}}}{2}}}$	10+254{displaystyle {frac {sqrt {10+2{sqrt {5}}}}{4}}} ${displaystyle {frac {sqrt {10+2{sqrt {5}}}}{4}}}$	2+22{displaystyle {frac {sqrt {2+{sqrt {2}}}}{2}}} $frac{sqrt{2+sqrt{2}}}{2}$	5+14{displaystyle {frac {{sqrt {5}}+1}{4}}} $frac{sqrt{5}+1}{4}$	10−254{displaystyle {frac {sqrt {10-2{sqrt {5}}}}{4}}} ${displaystyle {frac {sqrt {10-2{sqrt {5}}}}{4}}}$	2−22{displaystyle {frac {sqrt {2-{sqrt {2}}}}{2}}} $frac{sqrt{2-sqrt{2}}}{2}$	5−14{displaystyle {frac {{sqrt {5}}-1}{4}}} $frac{sqrt{5}-1}{4}$	2−32{displaystyle {frac {sqrt {2-{sqrt {3}}}}{2}}} ${displaystyle {frac {sqrt {2-{sqrt {3}}}}{2}}}$
tgα{displaystyle operatorname {tg} ,alpha } $operatorname{tg},alpha$	2−3{displaystyle 2-{sqrt {3}}} $2-sqrt{3}$	25−1055{displaystyle {frac {sqrt {25-10{sqrt {5}}}}{5}}} ${displaystyle {frac {sqrt {25-10{sqrt {5}}}}{5}}}$	2−1{displaystyle {sqrt {2}}-1} $sqrt{2}-1$	5−25{displaystyle {sqrt {5-2{sqrt {5}}}}} ${displaystyle {sqrt {5-2{sqrt {5}}}}}$	25+1055{displaystyle {frac {sqrt {25+10{sqrt {5}}}}{5}}} ${displaystyle {frac {sqrt {25+10{sqrt {5}}}}{5}}}$	2+1{displaystyle {sqrt {2}}+1} $sqrt{2}+1$	5+25{displaystyle {sqrt {5+2{sqrt {5}}}}} ${displaystyle {sqrt {5+2{sqrt {5}}}}}$	2+3{displaystyle 2+{sqrt {3}}} ${displaystyle 2+{sqrt {3}}}$
ctgα{displaystyle operatorname {ctg} ,alpha } $operatorname{ctg},alpha$	2+3{displaystyle 2+{sqrt {3}}} ${displaystyle 2+{sqrt {3}}}$	5+25{displaystyle {sqrt {5+2{sqrt {5}}}}} ${displaystyle {sqrt {5+2{sqrt {5}}}}}$	2+1{displaystyle {sqrt {2}}+1} $sqrt{2}+1$	25+1055{displaystyle {frac {sqrt {25+10{sqrt {5}}}}{5}}} ${displaystyle {frac {sqrt {25+10{sqrt {5}}}}{5}}}$	5−25{displaystyle {sqrt {5-2{sqrt {5}}}}} ${displaystyle {sqrt {5-2{sqrt {5}}}}}$	2−1{displaystyle {sqrt {2}}-1} $sqrt{2}-1$	25−1055{displaystyle {frac {sqrt {25-10{sqrt {5}}}}{5}}} ${displaystyle {frac {sqrt {25-10{sqrt {5}}}}{5}}}$	2−3{displaystyle 2-{sqrt {3}}} $2-sqrt{3}$
sec⁡α{displaystyle sec alpha } ${displaystyle sec alpha }$	22−3{displaystyle 2{sqrt {2-{sqrt {3}}}}} ${displaystyle 2{sqrt {2-{sqrt {3}}}}}$	50−1055{displaystyle {frac {sqrt {50-10{sqrt {5}}}}{5}}} ${displaystyle {frac {sqrt {50-10{sqrt {5}}}}{5}}}$	4−22{displaystyle {sqrt {4-2{sqrt {2}}}}} ${displaystyle {sqrt {4-2{sqrt {2}}}}}$	5−1{displaystyle {sqrt {5}}-1} ${displaystyle {sqrt {5}}-1}$	50+1055{displaystyle {frac {sqrt {50+10{sqrt {5}}}}{5}}} ${displaystyle {frac {sqrt {50+10{sqrt {5}}}}{5}}}$	4+22{displaystyle {sqrt {4+2{sqrt {2}}}}} ${displaystyle {sqrt {4+2{sqrt {2}}}}}$	5+1{displaystyle {sqrt {5}}+1} ${displaystyle {sqrt {5}}+1}$	22+3{displaystyle 2{sqrt {2+{sqrt {3}}}}} ${displaystyle 2{sqrt {2+{sqrt {3}}}}}$
cose cα{displaystyle operatorname {cosec} ,alpha } ${displaystyle operatorname {cosec} ,alpha }$	22+3{displaystyle 2{sqrt {2+{sqrt {3}}}}} ${displaystyle 2{sqrt {2+{sqrt {3}}}}}$	5+1{displaystyle {sqrt {5}}+1} ${displaystyle {sqrt {5}}+1}$	4+22{displaystyle {sqrt {4+2{sqrt {2}}}}} ${displaystyle {sqrt {4+2{sqrt {2}}}}}$	50+1055{displaystyle {frac {sqrt {50+10{sqrt {5}}}}{5}}} ${displaystyle {frac {sqrt {50+10{sqrt {5}}}}{5}}}$	5−1{displaystyle {sqrt {5}}-1} ${displaystyle {sqrt {5}}-1}$	4−22{displaystyle {sqrt {4-2{sqrt {2}}}}} ${displaystyle {sqrt {4-2{sqrt {2}}}}}$	50−1055{displaystyle {frac {sqrt {50-10{sqrt {5}}}}{5}}} ${displaystyle {frac {sqrt {50-10{sqrt {5}}}}{5}}}$	22−3{displaystyle 2{sqrt {2-{sqrt {3}}}}} ${displaystyle 2{sqrt {2-{sqrt {3}}}}}$

Значения тригонометрических функций для некоторых других углов

sin⁡π60=cos⁡29π60=sin⁡3∘=cos⁡87∘=2(3+1)(5−1)−2(3−1)5+516,{displaystyle sin {frac {pi }{60}}=cos {frac {29,pi }{60}}=sin 3^{circ }=cos 87^{circ }={frac {{sqrt {2}}({sqrt {3}}+1)({sqrt {5}}-1)-2({sqrt {3}}-1){sqrt {5+{sqrt {5}}}}}{16}},}

$sin frac{pi}{60} = cos frac{29,pi}{60} = sin 3^circ = cos 87^circ = frac{sqrt{2}(sqrt{3}+1)(sqrt{5}-1)-2(sqrt{3}-1)sqrt{5+sqrt{5}}}{16},$

cos⁡π60=sin⁡29π60=cos⁡3∘=sin⁡87∘=2(3−1)(5−1)+2(3+1)5+516,{displaystyle cos {frac {pi }{60}}=sin {frac {29,pi }{60}}=cos 3^{circ }=sin 87^{circ }={frac {{sqrt {2}}({sqrt {3}}-1)({sqrt {5}}-1)+2({sqrt {3}}+1){sqrt {5+{sqrt {5}}}}}{16}},}

$cos frac{pi}{60} = sin frac{29,pi}{60} = cos 3^circ = sin 87^circ = frac{sqrt{2}(sqrt{3}-1)(sqrt{5}-1)+2(sqrt{3}+1)sqrt{5+sqrt{5}}}{16},$

tg⁡π60=ctg⁡29π60=tg⁡3∘=ctg⁡87∘=2(5+2)−3(5+3)+(2−3)(3(5+1)−2)5−252,{displaystyle operatorname {tg} {frac {pi }{60}}=operatorname {ctg} {frac {29,pi }{60}}=operatorname {tg} 3^{circ }=operatorname {ctg} 87^{circ }={frac {2({sqrt {5}}+2)-{sqrt {3}}({sqrt {5}}+3)+(2-{sqrt {3}})({sqrt {3}}({sqrt {5}}+1)-2){sqrt {5-2{sqrt {5}}}}}{2}},}

$operatorname{tg} frac{pi}{60} = operatorname{ctg} frac{29,pi}{60} = operatorname{tg} 3^circ = operatorname{ctg} 87^circ = frac{2(sqrt{5}+2)-sqrt{3}(sqrt{5}+3)+(2-sqrt{3})(sqrt{3}(sqrt{5}+1)-2)sqrt{5-2sqrt{5}}}{2},$

ctg⁡π60=tg⁡29π60=ctg⁡3∘=tg⁡87∘=2(2(5+2)+3(5+3))+(3(5−1)+2)2(25+115)4,{displaystyle operatorname {ctg} {frac {pi }{60}}=operatorname {tg} {frac {29,pi }{60}}=operatorname {ctg} 3^{circ }=operatorname {tg} 87^{circ }={frac {2(2({sqrt {5}}+2)+{sqrt {3}}({sqrt {5}}+3))+({sqrt {3}}({sqrt {5}}-1)+2){sqrt {2(25+11{sqrt {5}})}}}{4}},}

$operatorname{ctg} frac{pi}{60} = operatorname{tg} frac{29,pi}{60} = operatorname{ctg} 3^circ = operatorname{tg} 87^circ = frac{2(2(sqrt{5}+2)+sqrt{3}(sqrt{5}+3))+(sqrt{3}(sqrt{5}-1)+2)sqrt{2(25+11sqrt{5})}}{4},$

sin⁡π30=cos⁡7π15=sin⁡6∘=cos⁡84∘=6(5−5)−5−18,{displaystyle sin {frac {pi }{30}}=cos {frac {7,pi }{15}}=sin 6^{circ }=cos 84^{circ }={frac {{sqrt {6(5-{sqrt {5}})}}-{sqrt {5}}-1}{8}},}

$sin frac{pi}{30} = cos frac{7,pi}{15} = sin 6^circ = cos 84^circ = frac{sqrt{6(5-sqrt{5})}-sqrt{5}-1}{8},$

cos⁡π30=sin⁡7π15=cos⁡6∘=sin⁡84∘=2(5−5)+3(5+1)8,{displaystyle cos {frac {pi }{30}}=sin {frac {7,pi }{15}}=cos 6^{circ }=sin 84^{circ }={frac {{sqrt {2(5-{sqrt {5}})}}+{sqrt {3}}({sqrt {5}}+1)}{8}},}

$cos frac{pi}{30} = sin frac{7,pi}{15} = cos 6^circ = sin 84^circ = frac{sqrt{2(5-sqrt{5})}+sqrt{3}(sqrt{5}+1)}{8},$

tg⁡π30=ctg⁡7π15=tg⁡6∘=ctg⁡84∘=2(5−5)−3(5−1)2,{displaystyle operatorname {tg} {frac {pi }{30}}=operatorname {ctg} {frac {7,pi }{15}}=operatorname {tg} 6^{circ }=operatorname {ctg} 84^{circ }={frac {{sqrt {2(5-{sqrt {5}})}}-{sqrt {3}}({sqrt {5}}-1)}{2}},}

$operatorname{tg} frac{pi}{30} = operatorname{ctg} frac{7,pi}{15} = operatorname{tg} 6^circ = operatorname{ctg} 84^circ = frac{sqrt{2(5-sqrt{5})}-sqrt{3}(sqrt{5}-1)}{2},$

ctg⁡π30=tg⁡7π15=ctg⁡6∘=tg⁡84∘=2(25+115)+3(5+3)2,{displaystyle operatorname {ctg} {frac {pi }{30}}=operatorname {tg} {frac {7,pi }{15}}=operatorname {ctg} 6^{circ }=operatorname {tg} 84^{circ }={frac {{sqrt {2(25+11{sqrt {5}})}}+{sqrt {3}}({sqrt {5}}+3)}{2}},}

$operatorname{ctg} frac{pi}{30} = operatorname{tg} frac{7,pi}{15} = operatorname{ctg} 6^circ = operatorname{tg} 84^circ = frac{sqrt{2(25+11sqrt{5})}+sqrt{3}(sqrt{5}+3)}{2},$

sin⁡π20=cos⁡9π20=sin⁡9∘=cos⁡81∘=2(5+1)−25−58,{displaystyle sin {frac {pi }{20}}=cos {frac {9,pi }{20}}=sin 9^{circ }=cos 81^{circ }={frac {{sqrt {2}}({sqrt {5}}+1)-2{sqrt {5-{sqrt {5}}}}}{8}},}

$sin frac{pi}{20} = cos frac{9,pi}{20} = sin 9^circ = cos 81^circ = frac{sqrt{2}(sqrt{5}+1)-2sqrt{5-sqrt{5}}}{8},$

cos⁡π20=sin⁡9π20=cos⁡9∘=sin⁡81∘=2(5+1)+25−58,{displaystyle cos {frac {pi }{20}}=sin {frac {9,pi }{20}}=cos 9^{circ }=sin 81^{circ }={frac {{sqrt {2}}({sqrt {5}}+1)+2{sqrt {5-{sqrt {5}}}}}{8}},}

$cos frac{pi}{20} = sin frac{9,pi}{20} = cos 9^circ = sin 81^circ = frac{sqrt{2}(sqrt{5}+1)+2sqrt{5-sqrt{5}}}{8},$

tg⁡π20=ctg⁡9π20=tg⁡9∘=ctg⁡81∘=5+1−5+25,{displaystyle operatorname {tg} {frac {pi }{20}}=operatorname {ctg} {frac {9,pi }{20}}=operatorname {tg} 9^{circ }=operatorname {ctg} 81^{circ }={{sqrt {5}}+1-{sqrt {5+2{sqrt {5}}}}},}

$operatorname{tg} frac{pi}{20} = operatorname{ctg} frac{9,pi}{20} = operatorname{tg} 9^circ = operatorname{ctg} 81^circ = {sqrt{5}+1-sqrt{5+2sqrt{5}}},$

ctg⁡π20=tg⁡9π20=ctg⁡9∘=tg⁡81∘=5+1+5+25,{displaystyle operatorname {ctg} {frac {pi }{20}}=operatorname {tg} {frac {9,pi }{20}}=operatorname {ctg} 9^{circ }=operatorname {tg} 81^{circ }={{sqrt {5}}+1+{sqrt {5+2{sqrt {5}}}}},}

$operatorname{ctg} frac{pi}{20} = operatorname{tg} frac{9,pi}{20} = operatorname{ctg} 9^circ = operatorname{tg} 81^circ = {sqrt{5}+1+sqrt{5+2sqrt{5}}},$

sin⁡π15=cos⁡13π30=sin⁡12∘=cos⁡78∘=2(5+5)−3(5−1)8,{displaystyle sin {frac {pi }{15}}=cos {frac {13,pi }{30}}=sin 12^{circ }=cos 78^{circ }={frac {{sqrt {2(5+{sqrt {5}})}}-{sqrt {3}}({sqrt {5}}-1)}{8}},}

$sin frac{pi}{15} = cos frac{13,pi}{30} = sin 12^circ = cos 78^circ = frac{sqrt{2(5+sqrt{5})}-sqrt{3}(sqrt{5}-1)}{8},$

cos⁡π15=sin⁡13π30=cos⁡12∘=sin⁡78∘=6(5+5)+5−18,{displaystyle cos {frac {pi }{15}}=sin {frac {13,pi }{30}}=cos 12^{circ }=sin 78^{circ }={frac {{sqrt {6(5+{sqrt {5}})}}+{sqrt {5}}-1}{8}},}

$cos frac{pi}{15} = sin frac{13,pi}{30} = cos 12^circ = sin 78^circ = frac{sqrt{6(5+sqrt{5})}+sqrt{5}-1}{8},$

tg⁡π15=ctg⁡13π30=tg⁡12∘=ctg⁡78∘=3(3−5)−2(25−115)2,{displaystyle operatorname {tg} {frac {pi }{15}}=operatorname {ctg} {frac {13,pi }{30}}=operatorname {tg} 12^{circ }=operatorname {ctg} 78^{circ }={frac {{sqrt {3}}(3-{sqrt {5}})-{sqrt {2(25-11{sqrt {5}})}}}{2}},}

$operatorname{tg} frac{pi}{15} = operatorname{ctg} frac{13,pi}{30} = operatorname{tg} 12^circ = operatorname{ctg} 78^circ = frac{sqrt{3}(3-sqrt{5})-sqrt{2(25-11sqrt{5})}}{2},$

ctg⁡π15=tg⁡13π30=ctg⁡12∘=tg⁡78∘=3(5+1)+2(5+5)2,{displaystyle operatorname {ctg} {frac {pi }{15}}=operatorname {tg} {frac {13,pi }{30}}=operatorname {ctg} 12^{circ }=operatorname {tg} 78^{circ }={frac {{sqrt {3}}({sqrt {5}}+1)+{sqrt {2(5+{sqrt {5}})}}}{2}},}

$operatorname{ctg} frac{pi}{15} = operatorname{tg} frac{13,pi}{30} = operatorname{ctg} 12^circ = operatorname{tg} 78^circ = frac{sqrt{3}(sqrt{5}+1)+sqrt{2(5+sqrt{5})}}{2},$

sin⁡7π60=cos⁡23π60=sin⁡21∘=cos⁡69∘=−2(3−1)(5+1)+2(3+1)5−516,{displaystyle sin {frac {7,pi }{60}}=cos {frac {23,pi }{60}}=sin 21^{circ }=cos 69^{circ }={frac {-{sqrt {2}}({sqrt {3}}-1)({sqrt {5}}+1)+2({sqrt {3}}+1){sqrt {5-{sqrt {5}}}}}{16}},}

$sin frac{7,pi}{60} = cos frac{23,pi}{60} = sin 21^circ = cos 69^circ = frac{-sqrt{2}(sqrt{3}-1)(sqrt{5}+1)+2(sqrt{3}+1)sqrt{5-sqrt{5}}}{16},$

cos⁡7π60=sin⁡23π60=cos⁡21∘=sin⁡69∘=2(3+1)(5+1)+2(3−1)5−516,{displaystyle cos {frac {7,pi }{60}}=sin {frac {23,pi }{60}}=cos 21^{circ }=sin 69^{circ }={frac {{sqrt {2}}({sqrt {3}}+1)({sqrt {5}}+1)+2({sqrt {3}}-1){sqrt {5-{sqrt {5}}}}}{16}},}

$cos frac{7,pi}{60} = sin frac{23,pi}{60} = cos 21^circ = sin 69^circ = frac{sqrt{2}(sqrt{3}+1)(sqrt{5}+1)+2(sqrt{3}-1)sqrt{5-sqrt{5}}}{16},$

tg⁡7π60=ctg⁡23π60=tg⁡21∘=ctg⁡69∘=2(2(5−2)−3(3−5))+(3(5+1)−2)2(25−115)4,{displaystyle operatorname {tg} {frac {7,pi }{60}}=operatorname {ctg} {frac {23,pi }{60}}=operatorname {tg} 21^{circ }=operatorname {ctg} 69^{circ }={frac {2(2({sqrt {5}}-2)-{sqrt {3}}(3-{sqrt {5}}))+({sqrt {3}}({sqrt {5}}+1)-2){sqrt {2(25-11{sqrt {5}})}}}{4}},}

$operatorname{tg} frac{7,pi}{60} = operatorname{ctg} frac{23,pi}{60} = operatorname{tg} 21^circ = operatorname{ctg} 69^circ = frac{2(2(sqrt{5}-2)-sqrt{3}(3-sqrt{5}))+(sqrt{3}(sqrt{5}+1)-2)sqrt{2(25-11sqrt{5})}}{4},$

ctg⁡7π60=tg⁡23π60=ctg⁡21∘=tg⁡69∘=2(2(5−2)+3(3−5))+(3(5+1)+2)2(25−115)4,{displaystyle operatorname {ctg} {frac {7,pi }{60}}=operatorname {tg} {frac {23,pi }{60}}=operatorname {ctg} 21^{circ }=operatorname {tg} 69^{circ }={frac {2(2({sqrt {5}}-2)+{sqrt {3}}(3-{sqrt {5}}))+({sqrt {3}}({sqrt {5}}+1)+2){sqrt {2(25-11{sqrt {5}})}}}{4}},}

$operatorname{ctg} frac{7,pi}{60} = operatorname{tg} frac{23,pi}{60} = operatorname{ctg} 21^circ = operatorname{tg} 69^circ = frac{2(2(sqrt{5}-2)+sqrt{3}(3-sqrt{5}))+(s qrt{3}(sqrt{5}+1)+2)sqrt{2(25-11sqrt{5})}}{4},$

sin⁡2π15=cos⁡11π30=sin⁡24∘=cos⁡66∘=3(5+1)−2(5−5)8,{displaystyle sin {frac {2,pi }{15}}=cos {frac {11,pi }{30}}=sin 24^{circ }=cos 66^{circ }={frac {{sqrt {3}}({sqrt {5}}+1)-{sqrt {2(5-{sqrt {5}})}}}{8}},}

$sin frac{2,pi}{15} = cos frac{11,pi}{30} = sin 24^circ = cos 66^circ = frac{sqrt{3}(sqrt{5}+1)-sqrt{2(5-sqrt{5})}}{8},$

cos⁡2π15=sin⁡11π30=cos⁡24∘=sin⁡66∘=5+1+6(5−5)8,{displaystyle cos {frac {2,pi }{15}}=sin {frac {11,pi }{30}}=cos 24^{circ }=sin 66^{circ }={frac {{sqrt {5}}+1+{sqrt {6(5-{sqrt {5}})}}}{8}},}

$cos frac{2,pi}{15} = sin frac{11,pi}{30} = cos 24^circ = sin 66^circ = frac{sqrt{5}+1+sqrt{6(5-sqrt{5})}}{8},$

tg⁡2π15=ctg⁡11π30=tg⁡24∘=ctg⁡66∘=−3(3+5)+2(25+115)2,{displaystyle operatorname {tg} {frac {2,pi }{15}}=operatorname {ctg} {frac {11,pi }{30}}=operatorname {tg} 24^{circ }=operatorname {ctg} 66^{circ }={frac {-{sqrt {3}}(3+{sqrt {5}})+{sqrt {2(25+11{sqrt {5}})}}}{2}},}

$operatorname{tg} frac{2,pi}{15} = operatorname{ctg} frac{11,pi}{30} = operatorname{tg} 24^circ = operatorname{ctg} 66^circ = frac{-sqrt{3}(3+sqrt{5})+sqrt{2(25+11sqrt{5})}}{2},$

ctg⁡2π15=tg⁡11π30=ctg⁡24∘=tg⁡66∘=3(5−1)+2(5−5)2,{displaystyle operatorname {ctg} {frac {2,pi }{15}}=operatorname {tg} {frac {11,pi }{30}}=operatorname {ctg} 24^{circ }=operatorname {tg} 66^{circ }={frac {{sqrt {3}}({sqrt {5}}-1)+{sqrt {2(5-{sqrt {5}})}}}{2}},}

$operatorname{ctg} frac{2,pi}{15} = operatorname{tg} frac{11,pi}{30} = operatorname{ctg} 24^circ = operatorname{tg} 66^circ = frac{sqrt{3}(sqrt{5}-1)+sqrt{2(5-sqrt{5})}}{2},$

sin⁡3π20=cos⁡7π20=sin⁡27∘=cos⁡63∘=−2(5−1)+25+58,{displaystyle sin {frac {3,pi }{20}}=cos {frac {7,pi }{20}}=sin 27^{circ }=cos 63^{circ }={frac {-{sqrt {2}}({sqrt {5}}-1)+2{sqrt {5+{sqrt {5}}}}}{8}},}

$sin frac{3,pi}{20} = cos frac{7,pi}{20} = sin 27^circ = cos 63^circ = frac{-sqrt{2}(sqrt{5}-1)+2sqrt{5+sqrt{5}}}{8},$

cos⁡3π20=sin⁡7π20=cos⁡27∘=sin⁡63∘=2(5−1)+25+58,{displaystyle cos {frac {3,pi }{20}}=sin {frac {7,pi }{20}}=cos 27^{circ }=sin 63^{circ }={frac {{sqrt {2}}({sqrt {5}}-1)+2{sqrt {5+{sqrt {5}}}}}{8}},}

$cos frac{3,pi}{20} = sin frac{7,pi}{20} = cos 27^circ = sin 63^circ = frac{sqrt{2}(sqrt{5}-1)+2sqrt{5+sqrt{5}}}{8},$

tg⁡3π20=ctg⁡7π20=tg⁡27∘=ctg⁡63∘=5−1−5−25,{displaystyle operatorname {tg} {frac {3,pi }{20}}=operatorname {ctg} {frac {7,pi }{20}}=operatorname {tg} 27^{circ }=operatorname {ctg} 63^{circ }={{sqrt {5}}-1-{sqrt {5-2{sqrt {5}}}}},}

$operatorname{tg} frac{3,pi}{20} = operatorname{ctg} frac{7,pi}{20} = operatorname{tg} 27^circ = operatorname{ctg} 63^circ = {sqrt{5}-1-sqrt{5-2sqrt{5}}},$

ctg⁡3π20=tg⁡7π20=ctg⁡27∘=tg⁡63∘=5−1+5−25,{displaystyle operatorname {ctg} {frac {3,pi }{20}}=operatorname {tg} {frac {7,pi }{20}}=operatorname {ctg} 27^{circ }=operatorname {tg} 63^{circ }={{sqrt {5}}-1+{sqrt {5-2{sqrt {5}}}}},}

$operatorname{ctg} frac{3,pi}{20} = operatorname{tg} frac{7,pi}{20} = operatorname{ctg} 27^circ = operatorname{tg} 63^circ = {sqrt{5}-1+sqrt{5-2sqrt{5}}},$

sin⁡11π60=cos⁡19π60=sin⁡33∘=cos⁡57∘=2(3+1)(5−1)+2(3−1)5+516,{displaystyle sin {frac {11,pi }{60}}=cos {frac {19,pi }{60}}=sin 33^{circ }=cos 57^{circ }={frac {{sqrt {2}}({sqrt {3}}+1)({sqrt {5}}-1)+2({sqrt {3}}-1){sqrt {5+{sqrt {5}}}}}{16}},}

$sin frac{11,pi}{60} = cos frac{19,pi}{60} = sin 33^circ = cos 57^circ = frac{sqrt{2}(sqrt{3}+1)(sqrt{5}-1)+2(sqrt{3}-1)sqrt{5+sqrt{5}}}{16},$

cos⁡11π60=sin⁡19π60=cos⁡33∘=sin⁡57∘=−2(3−1)(5−1)+2(3+1)5+516,{displaystyle cos {frac {11,pi }{60}}=sin {frac {19,pi }{60}}=cos 33^{circ }=sin 57^{circ }={frac {-{sqrt {2}}({sqrt {3}}-1)({sqrt {5}}-1)+2({sqrt {3}}+1){sqrt {5+{sqrt {5}}}}}{16}},}

$cos frac{11,pi}{60} = sin frac{19,pi}{60} = cos 33^circ = sin 57^circ = frac{-sqrt{2}(sqrt{3}-1)(sqrt{5}-1)+2(sqrt{3}+1)sqrt{5+sqrt{5}}}{16},$

tg⁡11π60=ctg⁡19π60=tg⁡33∘=ctg⁡57∘=−2(5+2)+3(3+5)+(2−3)(3(5+1)−2)5−252,{displaystyle operatorname {tg} {frac {11,pi }{60}}=operatorname {ctg} {frac {19,pi }{60}}=operatorname {tg} 33^{circ }=operatorname {ctg} 57^{circ }={frac {-2({sqrt {5}}+2)+{sqrt {3}}(3+{sqrt {5}})+(2-{sqrt {3}})({sqrt {3}}({sqrt {5}}+1)-2){sqrt {5-2{sqrt {5}}}}}{2}},}

$operatorname{tg} frac{11,pi}{60} = operatorname{ctg} frac{19,pi}{60} = operatorname{tg} 33^circ = operatorname{ctg} 57^circ = frac{-2(sqrt{5}+2)+sqrt{3}(3+sqrt{5})+(2-sqrt{3})(sqrt{3}(sqrt{5}+1)-2)sqrt{5-2sqrt{5}}}{2},$

ctg⁡11π60=tg⁡19π60=ctg⁡33∘=tg⁡57∘=−2(2(5+2)+3(3+5))+(3(5−1)+2)2(25+115)4,{displaystyle operatorname {ctg} {frac {11,pi }{60}}=operatorname {tg} {frac {19,pi }{60}}=operatorname {ctg} 33^{circ }=operatorname {tg} 57^{circ }={frac {-2(2({sqrt {5}}+2)+{sqrt {3}}(3+{sqrt {5}}))+({sqrt {3}}({sqrt {5}}-1)+2){sqrt {2(25+11{sqrt {5}})}}}{4}},}

$operatorname{ctg} frac{11,pi}{60} = operatorname{tg} frac{19,pi}{60} = operatorname{ctg} 33^circ = operatorname{tg} 57^circ = frac{-2(2(sqrt{5}+2)+sqrt{3}(3+sqrt{5}))+(sqrt{3}(sqrt{5}-1)+2)sqrt{2(25+11sqrt{5})}}{4},$

sin⁡13π60=cos⁡17π60=sin⁡39∘=cos⁡51∘=2(3+1)(5+1)−2(3−1)5−516,{displaystyle sin {frac {13,pi }{60}}=cos {frac {17,pi }{60}}=sin 39^{circ }=cos 51^{c
irc }={frac {{sqrt {2}}({sqrt {3}}+1)({sqrt {5}}+1)-2({sqrt {3}}-1){sqrt {5-{sqrt {5}}}}}{16}},}

$sin frac{13,pi}{60} = cos frac{17,pi}{60} = sin 39^circ = cos 51^circ = frac{sqrt{2}(sqrt{3}+1)(sqrt{5}+1)-2(sqrt{3}-1)sqrt{5-sqrt{5}}}{16},$

cos⁡13π60=sin⁡17π60=cos⁡39∘=sin⁡51∘=2(3−1)(5+1)+2(3+1)5−516,{displaystyle cos {frac {13,pi }{60}}=sin {frac {17,pi }{60}}=cos 39^{circ }=sin 51^{circ }={frac {{sqrt {2}}({sqrt {3}}-1)({sqrt {5}}+1)+2({sqrt {3}}+1){sqrt {5-{sqrt {5}}}}}{16}},}

$cos frac{13,pi}{60} = sin frac{17,pi}{60} = cos 39^circ = sin 51^circ = frac{sqrt{2}(sqrt{3}-1)(sqrt{5}+1)+2(sqrt{3}+1)sqrt{5-sqrt{5}}}{16},$

tg⁡13π60=ctg⁡17π60=tg⁡39∘=ctg⁡51∘=−2(2(5−2)+3(3−5))+(3(5+1)+2)2(25−115)4,{displaystyle operatorname {tg} {frac {13,pi }{60}}=operatorname {ctg} {frac {17,pi }{60}}=operatorname {tg} 39^{circ }=operatorname {ctg} 51^{circ }={frac {-2(2({sqrt {5}}-2)+{sqrt {3}}(3-{sqrt {5}}))+({sqrt {3}}({sqrt {5}}+1)+2){sqrt {2(25-11{sqrt {5}})}}}{4}},}

$operatorname{tg} frac{13,pi}{60} = operatorname{ctg} frac{17,pi}{60} = operatorname{tg} 39^circ = operatorname{ctg} 51^circ = frac{-2(2(sqrt{5}-2)+sqrt{3}(3-sqrt{5}))+(sqrt{3}(sqrt{5}+1)+2)sqrt{2(25-11sqrt{5})}}{4},$

ctg⁡13π60=tg⁡17π60=ctg⁡39∘=tg⁡51∘=−2(2(5−2)−3(3−5))+(3(5+1)−2)2(25−115)4,{displaystyle operatorname {ctg} {frac {13,pi }{60}}=operatorname {tg} {frac {17,pi }{60}}=operatorname {ctg} 39^{circ }=operatorname {tg} 51^{circ }={frac {-2(2({sqrt {5}}-2)-{sqrt {3}}(3-{sqrt {5}}))+({sqrt {3}}({sqrt {5}}+1)-2){sqrt {2(25-11{sqrt {5}})}}}{4}},}

$operatorname{ctg} frac{13,pi}{60} = operatorname{tg} frac{17,pi}{60} = operatorname{ctg} 39^circ = operatorname{tg} 51^circ = frac{-2(2(sqrt{5}-2)-sqrt{3}(3-sqrt{5}))+(sqrt{3}(sqrt{5}+1)-2)sqrt{2(25-11sqrt{5})}}{4},$

sin⁡7π30=cos⁡8π30=sin⁡42∘=cos⁡48∘=−(5−1)+6(5+5)8,{displaystyle sin {frac {7,pi }{30}}=cos {frac {8,pi }{30}}=sin 42^{circ }=cos 48^{circ }={frac {-({sqrt {5}}-1)+{sqrt {6(5+{sqrt {5}})}}}{8}},}

$sin frac{7,pi}{30} = cos frac{8,pi}{30} = sin 42^circ = cos 48^circ = frac{-(sqrt{5}-1)+sqrt{6(5+sqrt{5})}}{8},$

cos⁡7π30=sin⁡8π30=cos⁡42∘=sin⁡48∘=3(5−1)+2(5+5)8,{displaystyle cos {frac {7,pi }{30}}=sin {frac {8,pi }{30}}=cos 42^{circ }=sin 48^{circ }={frac {{sqrt {3}}({sqrt {5}}-1)+{sqrt {2(5+{sqrt {5}})}}}{8}},}

$cos frac{7,pi}{30} = sin frac{8,pi}{30} = cos 42^circ = sin 48^circ = frac{sqrt{3}(sqrt{5}-1)+sqrt{2(5+sqrt{5})}}{8},$

tg⁡7π30=ctg⁡8π30=tg⁡42∘=ctg⁡48∘=3(5+1)−2(5+5)2,{displaystyle operatorname {tg} {frac {7,pi }{30}}=operatorname {ctg} {frac {8,pi }{30}}=operatorname {tg} 42^{circ }=operatorname {ctg} 48^{circ }={frac {{sqrt {3}}({sqrt {5}}+1)-{sqrt {2(5+{sqrt {5}})}}}{2}},}

$operatorname{tg} frac{7,pi}{30} = operatorname{ctg} frac{8,pi}{30} = operatorname{tg} 42^circ = operatorname{ctg} 48^circ = frac{sqrt{3}(sqrt{5}+1)-sqrt{2(5+sqrt{5})}}{2},$

ctg⁡7π30=tg⁡8π30=ctg⁡42∘=tg⁡48∘=3(3−5)+2(25−115)2,{displaystyle operatorname {ctg} {frac {7,pi }{30}}=operatorname {tg} {frac {8,pi }{30}}=operatorname {ctg} 42^{circ }=operatorname {tg} 48^{circ }={frac {{sqrt {3}}(3-{sqrt {5}})+{sqrt {2(25-11{sqrt {5}})}}}{2}},}

$operatorname{ctg} frac{7,pi}{30} = operatorname{tg} frac{8,pi}{30} = operatorname{ctg} 42^circ = operatorname{tg} 48^circ = frac{sqrt{3}(3-sqrt{5})+sqrt{2(25-11sqrt{5})}}{2},$

tg⁡π120=ctg⁡59π120=tg⁡1.5∘=ctg⁡88.5∘=8−2(2−3)(3−5)−2(2+3)(5+5)8+2(2−3)(3−5)+2(2+3)(5+5),{displaystyle operatorname {tg} {frac {pi }{120}}=operatorname {ctg} {frac {59,pi }{120}}=operatorname {tg} 1.5^{circ }=operatorname {ctg} 88.5^{circ }={sqrt {frac {8-{sqrt {2(2-{sqrt {3}})(3-{sqrt {5}})}}-{sqrt {2(2+{sqrt {3}})(5+{sqrt {5}})}}}{8+{sqrt {2(2-{sqrt {3}})(3-{sqrt {5}})}}+{sqrt {2(2+{sqrt {3}})(5+{sqrt {5}})}}}}},}

$operatorname{tg} frac{pi}{120} = operatorname{ctg} frac{59,pi}{120} = operatorname{tg} 1.5^circ = operatorname{ctg} 88.5^circ = sqrt{frac{8-sqrt{2(2-sqrt{3})(3-sqrt{5})} - sqrt{ 2(2+sqrt{3})(5+sqrt{5})}}{8+sqrt{2(2-sqrt{3})(3-sqrt{5})}+sqrt{2(2+sqrt{3})(5+sqrt{5})} }},$

cos⁡π240=sin⁡119π240=cos⁡0.75∘=sin⁡89.25∘=116(2−2+2(2(5+5)+3(1−5))+2+2+2(6(5+5)+5−1)),{displaystyle cos {frac {pi }{240}}=sin {frac {119,pi }{240}}=cos 0.75^{circ }=sin 89.25^{circ }={frac {1}{16}}left({sqrt {2-{sqrt {2+{sqrt {2}}}}}}left({sqrt {2(5+{sqrt {5}})}}+{sqrt {3}}(1-{sqrt {5}})right)+{sqrt {2+{sqrt {2+{sqrt {2}}}}}}left({sqrt {6(5+{sqrt {5}})}}+{sqrt {5}}-1right)right),}

${displaystyle cos {frac {pi }{240}}=sin {frac {119,pi }{240}}=cos 0.75^{circ }=sin 89.25^{circ }={frac {1}{16}}left({sqrt {2-{sqrt {2+{sqrt {2}}}}}}left({sqrt {2(5+{sqrt {5}})}}+{sqrt {3}}(1-{sqrt {5}})right)+{sqrt {2+{sqrt {2+{sqrt {2}}}}}}left({sqrt {6(5+{sqrt {5}})}}+{sqrt {5}}-1right)right),}$

cos⁡π17=sin⁡15π34=182(2317−2(85+1917)+17+2(17−17)+17+15).{displaystyle cos {frac {pi }{17}}=sin {frac {15,pi }{34}}={frac {1}{8}}{sqrt {2left(2{sqrt {3{sqrt {17}}-{sqrt {2(85+19{sqrt {17}})}}+17}}+{sqrt {2(17-{sqrt {17}})}}+{sqrt {17}}+15right)}}.}

$cos frac{pi}{17} = sin frac{15,pi}{34} = frac{1}{8}sqrt{2 left(2sqrt{3sqrt{17}-sqrt{2(85+19sqrt{17})} +17}+sqrt{2(17-sqrt{17})}+sqrt{17}+15 right)}.$

sin⁡π2n+1=122−2+⋯+2⏟n,n∈N{displaystyle sin {pi over 2^{n+1}}={1 over 2}underbrace {sqrt {2-{sqrt {2+dots +{sqrt {2}}}}}} _{n},nin mathbb {N} }

${displaystyle sin {pi over 2^{n+1}}={1 over 2}underbrace {sqrt {2-{sqrt {2+dots +{sqrt {2}}}}}} _{n},nin mathbb {N} }$

cos⁡π2n+1=122+2+⋯+2⏟n,n∈N{displaystyle cos {pi over 2^{n+1}}={1 over 2}underbrace {sqrt {2+{sqrt {2+dots +{sqrt {2}}}}}} _{n},nin mathbb {N} }

${displaystyle cos {pi over 2^{n+1}}={1 over 2}underbrace {sqrt {2+{sqrt {2+dots +{sqrt {2}}}}}} _{n},nin mathbb {N} }$

sin⁡π3⋅2n=122−2+⋯+3⏟n,n≥2{displaystyle sin {pi over 3cdot 2^{n}}={1 over 2}underbrace {sqrt {2-{sqrt {2+dots +{sqrt {3}}}}}} _{n},ngeq 2}

${displaystyle sin {pi over 3cdot 2^{n}}={1 over 2}underbrace {sqrt {2-{sqrt {2+dots +{sqrt {3}}}}}} _{n},ngeq 2}$

cos⁡π3⋅2n=122+2+⋯+3⏟n,n≥2{displaystyle cos {pi over 3cdot 2^{n}}={1 over 2}underbrace {sqrt {2+{sqrt {2+dots +{sqrt {3}}}}}} _{n},ngeq 2}

${displaystyle cos {pi over 3cdot 2^{n}}={1 over 2}underbrace {sqrt {2+{sqrt {2+dots +{sqrt {3}}}}}} _{n},ngeq 2}$

Свойства тригонометрических функций

Простейшие тождества

Основная статья: Тригонометрические тождества

Поскольку синус и косинус являются соответственно ординатой и абсциссой точки, соответствующей на единичной окружности углу α, то, согласно уравнению единичной окружности (x2+y2=1{displaystyle x^{2}+y^{2}=1}

$x^{2}+y^{2}=1$ ) или теореме Пифагора, имеем:

sin2⁡α+cos2⁡α=1.{displaystyle sin ^{2}alpha +cos ^{2}alpha =1.}

{displaystyle sin ^{2}alpha +cos ^{2}alpha =1.}

Это соотношение называется основным тригонометрическим тождеством.

Разделив это уравнение на квадрат косинуса и синуса соответственно, получим:

1+tg2α=sec2α,{displaystyle 1+mathop {mathrm {tg} } ,^{2}alpha =mathop {mathrm {sec} } ,^{2}alpha ,}

{displaystyle 1+mathop {mathrm {tg} } ,^{2}alpha =mathop {mathrm {sec} } ,^{2}alpha ,}

1+ctg2α=cosec2α.{displaystyle 1+mathop {mathrm {ctg} } ,^{2}alpha =mathop {mathrm {cosec} } ,^{2}alpha .}

{displaystyle 1+mathop {mathrm {ctg} } ,^{2}alpha =mathop {mathrm {cosec} } ,^{2}alpha .}

Из определения тангенса и котангенса следует, что

tgα⋅ctgα=1.{displaystyle mathop {mathrm {tg} } ,alpha cdot mathop {mathrm {ctg} } ,alpha =1.}

mathop{mathrm{tg}},alpha cdot mathop{mathrm{ctg}},alpha=1.

Любую тригонометрическую функцию можно выразить через любую другую тригонометрическую функцию с тем же аргументом (с точностью до знака из-за неоднозначности раскрытия квадратного корня). Нижеприведённые формулы верны для 0<x<π/2{displaystyle 0<x<pi /2}

${displaystyle 0<x<pi /2}$ :

	sin	cos	tg	ctg	sec	cosec
sin⁡x={displaystyle ,sin x=} ${displaystyle ,sin x=}$	sin⁡x{displaystyle ,sin x} ${displaystyle ,sin x}$	1−cos2⁡x{displaystyle {sqrt {1-cos ^{2}x}}} ${displaystyle {sqrt {1-cos ^{2}x}}}$	tg⁡x1+tg2⁡x{displaystyle {frac {operatorname {tg} x}{sqrt {1+operatorname {tg} ^{2}x}}}} ${displaystyle {frac {operatorname {tg} x}{sqrt {1+operatorname {tg} ^{2}x}}}}$	1ctg2⁡x+1{displaystyle {frac {1}{sqrt {operatorname {ctg} ^{2}x+1}}}} ${displaystyle {frac {1}{sqrt {operatorname {ctg} ^{2}x+1}}}}$	sec2⁡x−1sec⁡x{displaystyle {frac {sqrt {sec ^{2}x-1}}{sec x}}} ${displaystyle {frac {sqrt {sec ^{2}x-1}}{sec x}}}$	1cosec⁡x{displaystyle {frac {1}{operatorname {cosec} x}}} ${displaystyle {frac {1}{operatorname {cosec} x}}}$
cos⁡x={displaystyle ,cos x=} ${displaystyle ,cos x=}$	1−sin2⁡x{displaystyle ,{sqrt {1-sin ^{2}x}}} ${displaystyle ,{sqrt {1-sin ^{2}x}}}$	cos⁡x{displaystyle ,cos x} ${displaystyle ,cos x}$	11+tg2⁡x{displaystyle ,{frac {1}{sqrt {1+operatorname {tg} ^{2}x}}}} ${displaystyle ,{frac {1}{sqrt {1+operatorname {tg} ^{2}x}}}}$	ctg⁡xctg2⁡x+1{displaystyle ,{frac {operatorname {ctg} x}{sqrt {operatorname {ctg} ^{2}x+1}}}} ${displaystyle ,{frac {operatorname {ctg} x}{sqrt {operatorname {ctg} ^{2}x+1}}}}$	1sec⁡x{displaystyle ,{frac {1}{sec x}}} ${displaystyle ,{frac {1}{sec x}}}$	cosec2⁡x−1cosec⁡x{displaystyle ,{frac {sqrt {operatorname {cosec} ^{2}x-1}}{operatorname {cosec} x}}} ${displaystyle ,{frac {sqrt {operatorname {cosec} ^{2}x-1}}{operatorname {cosec} x}}}$
tg⁡x={displaystyle ,operatorname {tg} x=} ${displaystyle ,operatorname {tg} x=}$	sin⁡x1−sin2⁡x{displaystyle ,{frac {sin x}{sqrt {1-sin ^{2}x}}}} ${displaystyle ,{frac {sin x}{sqrt {1-sin ^{2}x}}}}$	1−cos2⁡xcos⁡x{displaystyle ,{frac {sqrt {1-cos ^{2}x}}{cos x}}} ${displaystyle ,{frac {sqrt {1-cos ^{2}x}}{cos x}}}$	tg⁡x{displaystyle ,operatorname {tg} x} ${displaystyle ,operatorname {tg} x}$	1ctg⁡x{displaystyle ,{frac {1}{operatorname {ctg} x}}} ${displaystyle ,{frac {1}{operatorname {ctg} x}}}$	sec2⁡x−1{displaystyle ,{sqrt {sec ^{2}x-1}}} ${displaystyle ,{sqrt {sec ^{2}x-1}}}$	1cosec2⁡x−1{displaystyle ,{frac {1}{sqrt {operatorname {cosec} ^{2}x-1}}}} ${displaystyle ,{frac {1}{sqrt {operatorname {cosec} ^{2}x-1}}}}$
ctg⁡x={displaystyle ,operatorname {ctg} x=} ${displaystyle ,operatorname {ctg} x=}$	1−sin2⁡xsin⁡x{displaystyle ,{frac {sqrt {1-sin ^{2}x}}{sin x}}} ${displaystyle ,{frac {sqrt {1-sin ^{2}x}}{sin x}}}$	cos⁡x1−cos2⁡x{displaystyle ,{frac {cos x}{sqrt {1-cos ^{2}x}}}} ${displaystyle ,{frac {cos x}{sqrt {1-cos ^{2}x}}}}$	1tg⁡x{displaystyle ,{frac {1}{operatorname {tg} x}}} ${displaystyle ,{frac {1}{operatorname {tg} x}}}$	ctg⁡x{displaystyle ,operatorname {ctg} x} ${displaystyle ,operatorname {ctg} x}$	1sec2⁡x−1{displaystyle ,{frac {1}{sqrt {sec ^{2}x-1}}}} ${displaystyle ,{frac {1}{sqrt {sec ^{2}x-1}}}}$	cosec2⁡x−1{displaystyle ,{sqrt {operatorname {cosec} ^{2}x-1}}} ${displaystyle ,{sqrt {operatorname {cosec} ^{2}x-1}}}$
sec⁡x={displaystyle ,sec x=} ${displaystyle ,sec x=}$	11−sin2⁡x{displaystyle ,{frac {1}{sqrt {1-sin ^{2}x}}}} ${displaystyle ,{frac {1}{sqrt {1-sin ^{2}x}}}}$	1cos⁡x{displaystyle ,{frac {1}{cos x}}} ${displaystyle ,{frac {1}{cos x}}}$	1+tg2⁡x{displaystyle ,{sqrt {1+operatorname {tg} ^{2}x}}} ${displaystyle ,{sqrt {1+operatorname {tg} ^{2}x}}}$	ctg2⁡x+1ctg⁡x{displaystyle ,{frac {sqrt {operatorname {ctg} ^{2}x+1}}{operatorname {ctg} x}}} ${displaystyle ,{frac {sqrt {operatorname {ctg} ^{2}x+1}}{operatorname {ctg} x}}}$	sec⁡x{displaystyle ,sec x} ${displaystyle ,sec x}$	cosec⁡xcosec2⁡x−1{displaystyle ,{frac {operatorname {cosec} x}{sqrt {operatorname {cosec} ^{2}x-1}}}} ${displaystyle ,{frac {operatorname {cosec} x}{sqrt {operatorname {cosec} ^{2}x-1}}}}$
cosec⁡x={displaystyle ,operatorname {cosec} x=} ${displaystyle ,operatorname {cosec} x=}$	1sin⁡x{displaystyle ,{frac {1}{sin x}}} ${displaystyle ,{frac {1}{sin x}}}$	11−cos2⁡x{displaystyle ,{frac {1}{sqrt {1-cos ^{2}x}}}} ${displaystyle ,{frac {1}{sqrt {1-cos ^{2}x}}}}$	1+tg2⁡xtg⁡x{displaystyle ,{frac {sqrt {1+operatorname {tg} ^{2}x}}{operatorname {tg} x}}} ${displaystyle ,{frac {sqrt {1+operatorname {tg} ^{2}x}}{operatorname {tg} x}}}$	ctg2⁡x+1{displaystyle ,{sqrt {operatorname {ctg} ^{2}x+1}}} ${displaystyle ,{sqrt {operatorname {ctg} ^{2}x+1}}}$	sec⁡xsec2⁡x−1{displaystyle ,{frac {sec x}{sqrt {sec ^{2}x-1}}}} ${displaystyle ,{frac {sec x}{sqrt {sec ^{2}x-1}}}}$	cosec⁡x{displaystyle ,operatorname {cosec} x} ${displaystyle ,operatorname {cosec} x}$

Непрерывность

Синус и косинус — непрерывные функции.
Тангенс и секанс имеют точки разрыва π/2+πk{displaystyle pi /2+pi k} ${displaystyle pi /2+pi k}$ , где k{displaystyle k} $k$ — любое целое.
Котангенс и косеканс имеют точки разрыва πk{displaystyle pi k} ${displaystyle pi k}$ , где k{displaystyle k} $k$ — любое целое.

Чётность

Косинус и секанс — чётные. Остальные четыре функции — нечётные, то есть:

sin⁡(−α)=−sin⁡α,{displa
ystyle sin left(-alpha right)=-sin alpha ,,}

sin left( - alpha right) = - sin alpha ,,

cos⁡(−α)=cos⁡α,{displaystyle cos left(-alpha right)=cos alpha ,,}

cos left( - alpha right) = cos alpha ,,

tg(−α)=−tgα,{displaystyle mathop {mathrm {tg} } ,left(-alpha right)=-mathop {mathrm {tg} } ,alpha ,,}

mathop{mathrm{tg}}, left( - alpha right) = - mathop{mathrm{tg}}, alpha ,,

ctg(−α)=−ctgα,{displaystyle mathop {mathrm {ctg} } ,left(-alpha right)=-mathop {mathrm {ctg} } ,alpha ,,}

mathop{mathrm{ctg}}, left( - alpha right) = - mathop{mathrm{ctg}}, alpha ,,

sec⁡(−α)=sec⁡α,{displaystyle sec left(-alpha right)=sec alpha ,,}

sec left( - alpha right) = sec alpha ,,

cosec(−α)=−cosecα.{displaystyle mathop {mathrm {cosec} } ,left(-alpha right)=-mathop {mathrm {cosec} } ,alpha ,.}

mathop{mathrm{cosec}}, left( - alpha right) = - mathop{mathrm{cosec}}, alpha ,.

Периодичность

Функции sin⁡x,cos⁡x,sec⁡x,cosecx{displaystyle sin x,;cos x,;sec x,;mathrm {cosec} ,x}

${displaystyle sin x,;cos x,;sec x,;mathrm {cosec} ,x}$ — периодические с периодом 2π{displaystyle 2pi } $2pi$ , функции tgx{displaystyle mathrm {tg} ,x} ${displaystyle mathrm {tg} ,x}$ и ctgx{displaystyle mathrm {ctg} ,x} ${displaystyle mathrm {ctg} ,x}$ — c периодом π{displaystyle pi } $pi$ .

Формулы приведения

Формулами приведения называются формулы следующего вида:

f(nπ+α)=±f(α),{displaystyle f(npi +alpha )=pm f(alpha ),}

{displaystyle f(npi +alpha )=pm f(alpha ),}

f(nπ−α)=±f(α),{displaystyle f(npi -alpha )=pm f(alpha ),}

{displaystyle f(npi -alpha )=pm f(alpha ),}

f((2n+1)π2+α)=±g(α),{displaystyle fleft({frac {(2n+1)pi }{2}}+alpha right)=pm g(alpha ),}

{displaystyle fleft({frac {(2n+1)pi }{2}}+alpha right)=pm g(alpha ),}

f((2n+1)π2−α)=±g(α).{displaystyle fleft({frac {(2n+1)pi }{2}}-alpha right)=pm g(alpha ).}

{displaystyle fleft({frac {(2n+1)pi }{2}}-alpha right)=pm g(alpha ).}

Здесь f{displaystyle f}

$f$ — любая тригонометрическая функция, g{displaystyle g} $g$ — соответствующая ей кофункция (то есть косинус для синуса, синус для косинуса, тангенс для котангенса, котангенс для тангенса, секанс для косеканса и косеканс для секанса), n{displaystyle n} $n$ — целое число. Перед полученной функцией ставится тот знак, который имеет исходная функция в заданной координатной четверти при условии, что угол α{displaystyle alpha } $alpha$ острый, например:

cos⁡(π2−α)=sin⁡α,{displaystyle cos left({frac {pi }{2}}-alpha right)=sin alpha ,,}

cos left( frac{ pi}{2} - alpha right) = sin alpha,,

или что то же самое: cos⁡(90∘−α)=sin⁡α.{displaystyle cos left(90^{circ }-alpha right)=sin alpha ,.}

cos left( 90^circ - alpha right) = sin alpha,.

Некоторые формулы приведения:

α{displaystyle alpha } $alpha$	π2−α{displaystyle {frac {pi }{2}}-alpha } $frac{pi}{2} - alpha$	π2+α{displaystyle {frac {pi }{2}}+alpha } $frac{pi}{2} + alpha$	π−α{displaystyle pi -alpha } ${displaystyle pi -alpha }$	π+α{displaystyle pi +alpha } ${displaystyle pi +alpha }$	3π2−α{displaystyle {frac {3,pi }{2}}-alpha } $frac{3,pi}{2} - alpha$	3π2+α{displaystyle {frac {3,pi }{2}}+alpha } $frac{3,pi}{2} + alpha$	2π−α{displaystyle 2,pi -alpha } $2,pi - alpha$
sin⁡α{displaystyle sin alpha } $sinalpha$	cos⁡α{displaystyle cos alpha } $cosalpha$	cos⁡α{displaystyle cos alpha } $cosalpha$	sin⁡α{displaystyle sin alpha } $sinalpha$	−sin⁡α{displaystyle -sin alpha } ${displaystyle -sin alpha }$	−cos⁡α{displaystyle -cos alpha } ${displaystyle -cos alpha }$	−cos⁡α{displaystyle -cos alpha } ${displaystyle -cos alpha }$	−sin⁡α{displaystyle -sin alpha } ${displaystyle -sin alpha }$
cos⁡α{displaystyle cos alpha } $cosalpha$	sin⁡α{displaystyle sin alpha } $sinalpha$	−sin⁡α{displaystyle -sin alpha } ${displaystyle -sin alpha }$	−cos⁡α{displaystyle -cos alpha } ${displaystyle -cos alpha }$	−cos⁡α{displaystyle -cos alpha } ${displaystyle -cos alpha }$	−sin⁡α{displaystyle -sin alpha } ${displaystyle -sin alpha }$	sin⁡α{displaystyle sin alpha } $sinalpha$	cos⁡α{displaystyle cos alpha } $cosalpha$
tgα{displaystyle operatorname {tg} ,alpha } $operatorname{tg},alpha$	ctgα{displaystyle operatorname {ctg} ,alpha } $operatorname{ctg},alpha$	−ctgα{displaystyle -operatorname {ctg} ,alpha } $-operatorname{ctg},alpha$	−tgα{displaystyle -operatorname {tg} ,alpha } $-operatorname{tg},alpha$	tgα{displaystyle operatorname {tg} ,alpha } $operatorname{tg},alpha$	ctgα{displaystyle operatorname {ctg} ,alpha } $operatorname{ctg},alpha$	−ctgα{displaystyle -operatorname {ctg} ,alpha } $-operatorname{ctg},alpha$	−tgα{displaystyle -operatorname {tg} ,alpha } $-operatorname{tg},alpha$
ctgα{displaystyle operatorname {ctg} ,alpha } $operatorname{ctg},alpha$	tgα{displaystyle operatorname {tg} ,alpha } $operatorname{tg},alpha$	−tgα{displaystyle -operatorname {tg} ,alpha } $-operatorname{tg},alpha$	−ctgα{displaystyle -operatorname {ctg} ,alpha } $-operatorname{ctg},alpha$	ctgα{displaystyle operatorname {ctg} ,alpha } $operatorname{ctg},alpha$	tgα{displaystyle operatorname {tg} ,alpha } $operatorname{tg},alpha$	−tgα{displaystyle -operatorname {tg} ,alpha } $-operatorname{tg},alpha$	−ctgα{displaystyle -operatorname {ctg} ,alpha } $-operatorname{ctg},alpha$

Интересующие формулы приведения так же могут легко быть получены рассмотрением функций на единичной окружности.

Формулы сложения и вычитания

Значения тригонометрических функций суммы и разности двух углов:

sin⁡(α±β)=sin⁡αcos⁡β±cos⁡αsin⁡β,{displaystyle sin left(alpha pm beta right)=sin alpha ,cos beta pm cos alpha ,sin beta ,}

sinleft( alpha pm beta right)= sinalpha , cosbeta pm cosalpha , sinbeta,

cos⁡(α±β)=cos⁡αcos⁡β∓sin⁡αsin⁡β,{displaystyle cos left(alpha pm beta right)=cos alpha ,cos beta mp sin alpha ,sin beta ,}

cosleft( alpha pm beta right)= cosalpha , cosbeta mp sinalpha , sinbeta,

tg⁡(α±β)=tgα±tgβ1∓tgαtgβ,{displaystyle operatorname {tg} left(alpha pm beta right)={frac {operatorname {tg} ,alpha pm operatorname {tg} ,beta }{1mp operatorname {tg} ,alpha ,operatorname {tg} ,beta }},}

operatorname{tg}left( alpha pm beta right) = frac{operatorname{tg},alpha pm operatorname{tg},beta}{1 mp operatorname{tg},alpha , operatorname{tg},beta},

ctg⁡(α±β)=ctgαctgβ∓1ctgβ±ctgα.{displaystyle operatorname {ctg} left(alpha pm beta right)={frac {operatorname {ctg} ,alpha ,operatorname {ctg} ,beta mp 1}{operatorname {ctg} ,beta pm operatorname {ctg} ,alpha }}.}

operatorname{ctg}left( alpha pm beta right) = frac{operatorname{ctg},alpha,operatorname{ctg},beta mp 1}{operatorname{ctg},beta pm operatorname{ctg},alpha}.

Аналогичные формулы для суммы трёх углов:

sin⁡(α+β+γ)=sin⁡αcos⁡βcos⁡γ+cos⁡αsin⁡βcos⁡γ+cos⁡αcos⁡βsin⁡γ−sin⁡αsin⁡βsin⁡γ,{displaystyle sin left(alpha +beta +gamma right)=sin alpha cos beta cos gamma +cos alpha sin beta cos gamma +cos alpha cos beta sin gamma -sin alpha sin beta sin gamma ,}

sin left( alpha + beta + gamma right) = sin alpha cos beta cos gamma + cos alpha sin beta cos gamma + cos alpha cos beta sin gamma - sin alpha sin beta sin gamma,

cos⁡(α+β+γ)=cos⁡αcos⁡βcos⁡γ−sin⁡αsin⁡βcos⁡γ−sin⁡αcos⁡βsin⁡γ−cos⁡αsin⁡βsin⁡γ.{displaystyle cos left(alpha +beta +gamma right)=cos alpha cos beta cos gamma -sin alpha sin beta cos gamma -sin alpha cos beta sin gamma -cos alpha sin beta sin gamma .}

cos left( alpha + beta + gamma right) = cos alpha cos beta cos gamma - sin alpha sin beta cos gamma - sin alpha cos beta sin gamma - cos alpha sin beta sin gamma.

Формулы для кратных углов

Формулы двойного угла:

sin⁡2α=2sin⁡αcos⁡α=2tgα1+tg2⁡α=2ctgα1+ctg2⁡α=2tgα+ctgα,{displaystyle sin 2alpha =2sin alpha cos alpha ={frac {2,operatorname {tg} ,alpha }{1+operatorname {tg} ^{2}alpha }}={frac {2,operatorname {ctg} ,alpha }{1+operatorname {ctg} ^{2}alpha }}={frac {2}{operatorname {tg} ,alpha +operatorname {ctg} ,alpha }},}

sin 2alpha = 2 sin alpha cos alpha = frac{2,operatorname{tg},alpha }{1 + operatorname{tg}^2alpha} = frac{2,operatorname{ctg},alpha }{1 + operatorname{ctg}^2alpha} = frac{2}{operatorname{tg},alpha + operatorname{ctg},alpha},

cos⁡2α=cos2⁡α−sin2⁡α=2cos2⁡α−1=1−2sin2⁡α=1−tg2⁡α1+tg2⁡α=ctg2⁡α−1ctg2⁡α+1=ctgα−tgαctgα+tgα,{displaystyle cos 2alpha =cos ^{2}alpha ,-,sin ^{2}alpha =2cos ^{2}alpha ,-,1=1,-,2sin ^{2}alpha ={frac {1-operatorname {tg} ^{2}alpha }{1+operatorname {tg} ^{2}alpha }}={frac {operatorname {ctg} ^{2}alpha -1}{operatorname {ctg} ^{2}alpha +1}}={frac {operatorname {ctg} ,alpha -operatorname {tg} ,alpha }{operatorname {ctg} ,alpha +operatorname {tg} ,alpha }},}

cos 2alpha = cos^2 alpha,-,sin^2 alpha = 2 cos^2 alpha,-,1 = 1,-,2 sin^2 alpha = frac{1 - operatorname{tg}^2 alpha}{1 + operatorname{tg}^2alpha} = frac{operatorname{ctg}^2 alpha - 1}{operatorname{ctg}^2alpha + 1} = frac{operatorname{ctg},alpha - operatorname{tg},alpha}{operatorname{ctg},alpha + operatorname{tg},alpha},

tg2α=2tgα1−tg2⁡α=2ctgαctg2⁡α−1=2ctgα−tgα,{displaystyle operatorname {tg} ,2alpha ={frac {2,operatorname {tg} ,alpha }{1-operatorname {tg} ^{2}alpha }}={frac {2,operatorname {ctg} ,alpha }{operatorname {ctg} ^{2}alpha -1}}={frac {2}{operatorname {ctg} ,alpha -operatorname {tg} ,alpha }},}

operatorname{tg},2 alpha = frac{2,operatorname{tg},alpha}{1 - operatorname{tg}^2alpha} = frac{2,operatorname{ctg},alpha}{operatorname{ctg}^2alpha - 1} = frac{2}{operatorname{ctg},alpha - operatorname{tg},alpha},

ctg2α=ctg2⁡α−12ctgα=ctgα−tgα2.{displaystyle operatorname {ctg} ,2alpha ={frac {operatorname {ctg} ^{2}alpha -1}{2,operatorname {ctg} ,alpha }}={frac {operatorname {ctg} ,alpha -operatorname {tg} ,alpha }{2}}.}

operatorname{ctg},2 alpha = frac{operatorname{ctg}^2 alpha - 1}{2,operatorname{ctg},alpha} = frac{operatorname{ctg},alpha - operatorname{tg},alpha}{2}.

Формулы тройного угла:

sin3α=3sin⁡α−4sin3⁡α,{displaystyle sin ,3alpha =3sin alpha -4sin ^{3}alpha ,}

sin,3alpha=3sinalpha - 4sin^3alpha,

cos3α=4cos3⁡α−3cos⁡α,{displaystyle cos ,3alpha =4cos ^{3}alpha -3cos alpha ,}

cos,3alpha=4cos^3alpha -3cosalpha,

tg3α=3tgα−tg3α1−3tg2α,{displaystyle operatorname {tg} ,3alpha ={frac {3,operatorname {tg} ,alpha -operatorname {tg} ^{3},alpha }{1-3,operatorname {tg} ^{2},alpha }},}

operatorname{tg},3alpha=frac{3,operatorname{tg},alpha - operatorname{tg}^3,alpha}{1 - 3,operatorname{tg}^2,alpha},

ctg3α=ctg3α−3ctgα3ctg2α−1.{displaystyle operatorname {ctg} ,3alpha ={frac {operatorname {ctg} ^{3},alpha -3,operatorname {ctg} ,alpha }{3,operatorname {ctg} ^{2},alpha -1}}.}

operatorname{ctg},3alpha=frac{operatorname{ctg}^3,alpha - 3,operatorname{ctg},alpha}{3,operatorname{ctg}^2,alpha - 1}.

Прочие формулы для кратных углов:

sin4α=cos⁡α(4sin⁡α−8sin3⁡α),{displaystyle sin ,4alpha =cos alpha left(4sin alpha -8sin ^{3}alpha right),}

sin,4alpha=cosalpha left(4sinalpha - 8sin^3alpharight),

cos4α=8cos4⁡α−8cos2⁡α+1,{displaystyle cos ,4alpha =8cos ^{4}alpha -8cos ^{2}alpha +1,}

cos,4alpha=8cos^4alpha - 8cos^2alpha + 1,

tg4α=4tgα−4tg3α1−6tg2α+tg4α,{displaystyle operatorname {tg} ,4alpha ={frac {4,operatorname {tg} ,alpha -4,operatorname {tg} ^{3},alpha }{1-6,operatorname {tg} ^{2},alpha +operatorname {tg} ^{4},alpha }},}

operatorname{tg},4alpha=frac{4,operatorname{tg},alpha - 4,operatorname{tg}^3,alpha}{1 - 6,operatorname{tg}^2,alpha + operatorname{tg}^4,alpha},

ctg4α=ctg4α−6ctg2α+14ctg3α−4ctgα,{displaystyle operatorname {ctg} ,4alpha ={frac {operatorname {ctg} ^{4},alpha -6,operatorname {ctg} ^{2},alpha +1}{4,operatorname {ctg} ^{3},alpha -4,operatorname {ctg} ,alpha }},}

operatorname{ctg},4alpha=frac{operatorname{ctg} ^4,alpha - 6,operatorname{ctg}^2,alpha + 1}{4,operatorname{ctg}^3,alpha - 4,operatorname{ctg},alpha},

sin5α=16sin5⁡α−20sin3⁡α+5sin⁡α,{displaystyle sin ,5alpha =16sin ^{5}alpha -20sin ^{3}alpha +5sin alpha ,}

sin,5alpha=16sin^5alpha-20sin^3alpha +5sinalpha,

cos5α=16cos5⁡α−20cos3⁡α+5cos⁡α,{displaystyle cos ,5alpha =16cos ^{5}alpha -20cos ^{3}alpha +5cos alpha ,}

cos,5alpha=16cos^5alpha-20cos^3alpha +5cosalpha,

tg5α=tg⁡αtg4⁡α−10tg2⁡α+55tg4⁡α−10tg2⁡α+1,{displaystyle operatorname {tg} ,5alpha =operatorname {tg} alpha {frac {operatorname {tg} ^{4}alpha -10operatorname {tg} ^{2}alpha +5}{5operatorname {tg} ^{4}alpha -10operatorname {tg} ^{2}alpha +1}},}

operatorname{tg},5alpha=operatorname{tg}alphafrac{operatorname{tg}^4alpha-10operatorname{tg}^2alpha+5}{5operatorname{tg}^4alpha-10operatorname{tg}^2alpha+1},

ctg5α=ctg⁡αctg4⁡α−10ctg2⁡α+55ctg4⁡α−10ctg2⁡α+1,{displaystyle operatorname {ctg} ,5alpha =operatorname {ctg} alpha {frac {operatorname {ctg} ^{4}alpha -10operatorname {ctg} ^{2}alpha +5}{5operatorname {ctg} ^{4}alpha -10operatorname {ctg} ^{2}alpha +1}},}

operatorname{ctg},5alpha=operatorname{ctg}alphafrac{operatorname{ctg}^4alpha-10operatorname{ctg}^2alpha+5}{5operatorname{ctg}^4alpha-10operatorname{ctg}^2alpha+1},

sin⁡(nα)=2n−1∏k=0n−1sin⁡(α+πkn){displaystyle sin(nalpha )=2^{n-1}prod _{k=0}^{n-1}sin left(alpha +{frac {pi k}{n}}right)}

sin (nalpha)=2^{n-1}prod^{n-1}_{k=0}sinleft( alpha+frac{pi k}{n}right)

следует из формулы дополнения и формулы Гаусса для гамма-функции.

Из формулы Муавра можно получить следующие общие выражения для кратных углов:

sin⁡(nα)=∑k=0[(n−1)/2](−1)k(n2k+1)cosn−2k−1⁡αsin2k+1⁡α,{displaystyle sin(nalpha )=sum _{k=0}^{[(n-1)/2]}(-1)^{k}{binom {n}{2k+1}}cos ^{n-2k-1}alpha ,sin ^{2k+1}alpha ,}

sin(nalpha)=sum_{k=0}^{[(n-1)/2]}(-1)^kbinom{n}{2k+1}cos^{n-2k-1}alpha,sin^{2k+1}alpha,

cos⁡(nα)=∑k=0[n/2](−1)k(n2k)cosn−2k⁡αsin2k⁡α,{displaystyle cos(nalpha )=sum _{k=0}^{[n/2]}(-1)^{k}{binom {n}{2k}}cos ^{n-2k}alpha ,sin ^{2k}alpha ,}

cos(nalpha)=sum_{k=0}^{[n/2]}(-1)^kbinom{n}{2k}cos^{n-2k}alpha,sin^{2k}alpha,

tg(nα)=sin⁡(nα)cos⁡(nα)=∑k=0[(n−1)/2](−1)k(n2k+1)tg2k+1α∑k=0[n/2](−1)k(n2k)tg2kα,{displaystyle mathrm {tg} (nalpha )={frac {sin(nalpha )}{cos(nalpha )}}={dfrac {displaystyle {sum limits _{k=0}^{[(n-1)/2]}(-1)^{k}{binom {n}{2k+1}}mathrm {tg} ^{2k+1}alpha }}{displaystyle {sum limits _{k=0}^{[n/2]}(-1)^{k}{binom {n}{2k}}mathrm {tg} ^{2k}alpha }}},}

mathrm{tg}(nalpha)=frac{sin(nalpha)}{cos(nalpha)}=dfrac{displaystyle{sumlimits_{k=0}^{[(n-1)/2]}(-1)^kbinom{n}{2k+1}mathrm{tg}^{2k+1}alpha}}{displaystyle{sumlimits_{k=0}^{[n/2]}(-1)^kbinom{n}{2k}mathrm{tg}^{2k}alpha}},

ctg(nα)=cos⁡(nα)sin⁡(nα)=∑k=0[n/2](−1)k(n2k)ctgn−2kα∑k=0[(n−1)/2](−1)k(n2k+1)ctgn−2k−1α,{displaystyle mathrm {ctg} (nalpha )={frac {cos(nalpha )}{sin(nalpha )}}={dfrac {displaystyle {sum limits _{k=0}^{[n/2]}(-1)^{k}{binom {n}{2k}}mathrm {ctg} ^{n-2k}alpha }}{displaystyle {sum limits _{k=0}^{[(n-1)/2]}(-1)^{k}{binom {n}{2k+1}}mathrm {ctg} ^{n-2k-1}alpha }}},}

mathrm{ctg}(nalpha)=frac{cos(nalpha)}{sin(nalpha)}=dfrac{displaystyle{sumlimits_{k=0}^{[n/2]}(-1)^kbinom{n}{2k}mathrm{ctg}^{n-2k}alpha}}{displaystyle{sumlimits_{k=0}^{[(n-1)/2]}(-1)^kbinom{n}{2k+1}mathrm{ctg}^{n-2k-1}alpha}},

где [n]{displaystyle [n]}

$[n]$ — целая часть числа n{displaystyle n} $n$ , (nk){displaystyle {binom {n}{k}}} $binom{n}{k}$ — биномиальный коэффициент.

Формулы половинного угла:

sin⁡α2=1−cos⁡α2,0⩽α⩽2π,{displaystyle sin {frac {alpha }{2}}={sqrt {frac {1-cos alpha }{2}}},quad 0leqslant alpha leqslant 2pi ,}

sinfrac{alpha}{2}=sqrt{frac{1-cosalpha}{2}},quad 0 leqslant alpha leqslant 2pi,

cos⁡α2=1+cos⁡α2,−π⩽α⩽π,{displaystyle cos {frac {alpha }{2}}={sqrt {frac {1+cos alpha }{2}}},quad -pi leqslant alpha leqslant p
i ,}

cosfrac{alpha}{2}=sqrt{frac{1+cosalpha}{2}},quad -pi leqslant alpha leqslant pi,

tgα2=1−cos⁡αsin⁡α=sin⁡α1+cos⁡α,{displaystyle operatorname {tg} ,{frac {alpha }{2}}={frac {1-cos alpha }{sin alpha }}={frac {sin alpha }{1+cos alpha }},}

operatorname{tg},frac{alpha}{2}=frac{1-cosalpha}{sinalpha}=frac{sinalpha}{1+cosalpha},

ctgα2=sin⁡α1−cos⁡α=1+cos⁡αsin⁡α,{displaystyle operatorname {ctg} ,{frac {alpha }{2}}={frac {sin alpha }{1-cos alpha }}={frac {1+cos alpha }{sin alpha }},}

operatorname{ctg},frac{alpha}{2}=frac{sinalpha}{1-cosalpha}=frac{1+cosalpha}{sinalpha},

tgα2=1−cos⁡α1+cos⁡α,0⩽α<π,{displaystyle operatorname {tg} ,{frac {alpha }{2}}={sqrt {frac {1-cos alpha }{1+cos alpha }}},quad 0leqslant alpha <pi ,}

operatorname{tg},frac{alpha}{2}=sqrt{frac{1-cosalpha}{1+cosalpha}},quad 0 leqslant alpha < pi,

ctgα2=1+cos⁡α1−cos⁡α,0<α⩽π.{displaystyle operatorname {ctg} ,{frac {alpha }{2}}={sqrt {frac {1+cos alpha }{1-cos alpha }}},quad 0<alpha leqslant pi .}

operatorname{ctg},frac{alpha}{2}=sqrt{frac{1+cosalpha}{1-cosalpha}},quad 0 < alpha leqslant pi.

Произведения

Формулы для произведений функций двух углов:

sin⁡αsin⁡β=cos⁡(α−β)−cos⁡(α+β)2,{displaystyle sin alpha sin beta ={frac {cos(alpha -beta )-cos(alpha +beta )}{2}},}

sin alpha sin beta ={frac {cos(alpha -beta )-cos(alpha +beta )}{2}},

sin⁡αcos⁡β=sin⁡(α−β)+sin⁡(α+β)2,{displaystyle sin alpha cos beta ={frac {sin(alpha -beta )+sin(alpha +beta )}{2}},}

sinalpha cosbeta = frac{sin(alpha-beta) + sin(alpha+beta)}{2},

cos⁡αcos⁡β=cos⁡(α−β)+cos⁡(α+β)2,{displaystyle cos alpha cos beta ={frac {cos(alpha -beta )+cos(alpha +beta )}{2}},}

cosalpha cosbeta = frac{cos(alpha-beta) + cos(alpha+beta)}{2},

tgαtgβ=cos⁡(α−β)−cos⁡(α+β)cos⁡(α−β)+cos⁡(α+β),{displaystyle operatorname {tg} ,alpha ,operatorname {tg} ,beta ={frac {cos(alpha -beta )-cos(alpha +beta )}{cos(alpha -beta )+cos(alpha +beta )}},}

operatorname{tg},alpha,operatorname{tg},beta = frac{cos(alpha-beta) - cos(alpha+beta)}{cos(alpha-beta) + cos(alpha+beta)},

tgαctgβ=sin⁡(α−β)+sin⁡(α+β)sin⁡(α+β)−sin⁡(α−β),{displaystyle operatorname {tg} ,alpha ,operatorname {ctg} ,beta ={frac {sin(alpha -beta )+sin(alpha +beta )}{sin(alpha +beta )-sin(alpha -beta )}},}

operatorname{tg},alpha,operatorname{ctg},beta = frac{sin(alpha-beta) + sin(alpha+beta)}{sin(alpha+beta) -sin(alpha-beta)},

ctgαctgβ=cos⁡(α−β)+cos⁡(α+β)cos⁡(α−β)−cos⁡(α+β).{displaystyle operatorname {ctg} ,alpha ,operatorname {ctg} ,beta ={frac {cos(alpha -beta )+cos(alpha +beta )}{cos(alpha -beta )-cos(alpha +beta )}}.}

operatorname{ctg},alpha,operatorname{ctg},beta = frac{cos(alpha-beta) + cos(alpha+beta)}{cos(alpha-beta) - cos(alpha+beta)}.

Аналогичные формулы для произведений синусов и косинусов трёх углов:

sin⁡αsin⁡βsin⁡γ=sin⁡(α+β−γ)+sin⁡(β+γ−α)+sin⁡(α−β+γ)−sin⁡(α+β+γ)4,{displaystyle sin alpha sin beta sin gamma ={frac {sin(alpha +beta -gamma )+sin(beta +gamma -alpha )+sin(alpha -beta +gamma )-sin(alpha +beta +gamma )}{4}},}

sinalpha sinbeta singamma = frac{sin(alpha+beta-gamma) + sin(beta+gamma-alpha) + sin(alpha-beta+gamma) - sin(alpha+beta+gamma)}{4},

sin⁡αsin⁡βcos⁡γ=−cos⁡(α+β−γ)+cos⁡(β+γ−α)+cos⁡(α−β+γ)−cos⁡(α+β+γ)4,{displaystyle sin alpha sin beta cos gamma ={frac {-cos(alpha +beta -gamma )+cos(beta +gamma -alpha )+cos(alpha -beta +gamma )-cos(alpha +beta +gamma )}{4}},}

sinalpha sinbeta cosgamma = frac{-cos(alpha+beta-gamma) + cos(beta+gamma-alpha) + cos(alpha-beta+gamma) - cos(alpha+beta+gamma)}{4},

sin⁡αcos⁡βcos⁡γ=sin⁡(α+β−γ)−sin⁡(β+γ−α)+sin⁡(α−β+γ)−sin⁡(α+β+γ)4,{displaystyle sin alpha cos beta cos gamma ={frac {sin(alpha +beta -gamma )-sin(beta +gamma -alpha )+sin(alpha -beta +gamma )-sin(alpha +beta +gamma )}{4}},}

sinalpha cosbeta cosgamma = frac{sin(alpha+beta-gamma) - sin(beta+gamma-alpha) + sin(alpha-beta+gamma) - sin(alpha+beta+gamma)}{4},

cos⁡αcos⁡βcos⁡γ=cos⁡(α+β−γ)+cos⁡(β+γ−α)+cos⁡(α−β+γ)+cos⁡(α+β+γ)4.{displaystyle cos alpha cos beta cos gamma ={frac {cos(alpha +beta -gamma )+cos(beta +gamma -alpha )+cos(alpha -beta +gamma )+cos(alpha +beta +gamma )}{4}}.}

cosalpha cosbeta cosgamma = frac{cos(alpha+beta-gamma) + cos(beta+gamma-alpha) + cos(alpha-beta+gamma) + cos(alpha+beta+gamma)}{4}.

Формулы для произведений тангенсов и котангенсов трёх углов можно получить, поделив правые и левые части соответствующих равенств, представленных выше.

Степени

sin2⁡α=1−cos⁡2α2=tg2α1+tg2α,{displaystyle sin ^{2}alpha ={frac {1-cos 2,alpha }{2}}={frac {operatorname {tg} ^{2},alpha }{1+operatorname {tg} ^{2},alpha }},}

{displaystyle sin ^{2}alpha ={frac {1-cos 2,alpha }{2}}={frac {operatorname {tg} ^{2},alpha }{1+operatorname {tg} ^{2},alpha }},}

cos2⁡α=1+cos⁡2α2=ctg2α1+ctg2α,{displaystyle cos ^{2}alpha ={frac {1+cos 2,alpha }{2}}={frac {operatorname {ctg} ^{2},alpha }{1+operatorname {ctg} ^{2},alpha }},}

cos ^{2}alpha ={frac {1+cos 2,alpha }{2}}={frac {operatorname {ctg}^{2},alpha }{1+operatorname {ctg}^{2},alpha }},

tg2α=1−cos⁡2α1+cos⁡2α=sin2α1−sin2α,{displaystyle operatorname {tg} ^{2},alpha ={frac {1-cos 2,alpha }{1+cos 2,alpha }}={frac {operatorname {sin} ^{2},alpha }{1-operatorname {sin} ^{2},alpha }},}

operatorname {tg}^{2},alpha ={frac {1-cos 2,alpha }{1+cos 2,alpha }}={frac {operatorname {sin}^{2},alpha }{1-operatorname {sin}^{2},alpha }},

ctg2α=1+cos⁡2α1−cos⁡2α,=cos2α1−cos2α,{displaystyle operatorname {ctg} ^{2},alpha ={frac {1+cos 2,alpha }{1-cos 2,alpha }},={frac {operatorname {cos} ^{2},alpha }{1-operatorname {cos} ^{2},alpha }},}

operatorname {ctg}^{2},alpha ={frac {1+cos 2,alpha }{1-cos 2,alpha }},={frac {operatorname {cos}^{2},alpha }{1-operatorname {cos}^{2},alpha }},

sin3⁡α=3sin⁡α−sin⁡3α4,{displaystyle sin ^{3}alpha ={frac {3sin alpha -sin 3,alpha }{4}},}

sin^3alpha = frac{3sinalpha - sin 3,alpha}{4},

cos3⁡α=3cos⁡α+cos⁡3α4,{displaystyle cos ^{3}alpha ={frac {3cos alpha +cos 3,alpha }{4}},}

cos^3alpha = frac{3cosalpha + cos 3,alpha}{4},

tg3α=3sin⁡α−sin⁡3α3cos⁡α+cos⁡3α,{displaystyle operatorname {tg} ^{3},alpha ={frac {3sin alpha -sin 3,alpha }{3cos alpha +cos 3,alpha }},}

operatorname{tg}^3,alpha = frac{3sinalpha - sin 3,alpha}{3cosalpha + cos 3,alpha},

ctg3α=3cos⁡α+cos⁡3α3sin⁡α−sin⁡3α,{displaystyle operatorname {ctg} ^{3},alpha ={frac {3cos alpha +cos 3,alpha }{3sin alpha -sin 3,alpha }},}

operatorname{ctg}^3,alpha = frac{3cosalpha + cos 3,alpha}{3sinalpha - sin 3,alpha},

sin4⁡α=cos⁡4α−4cos⁡2α+38,{displaystyle sin ^{4}alpha ={frac {cos 4alpha -4cos 2,alpha +3}{8}},}

sin^4alpha = frac{cos 4alpha - 4cos 2,alpha + 3}{8},

cos4⁡α=cos⁡4α+4cos⁡2α+38,{displaystyle cos ^{4}alpha ={frac {cos 4alpha +4cos 2,alpha +3}{8}},}

cos^4alpha = frac{cos 4alpha + 4cos 2,alpha + 3}{8},

tg4α=cos⁡4α−4cos⁡2α+3cos⁡4α+4cos⁡2α+3,{displaystyle operatorname {tg} ^{4},alpha ={frac {cos 4alpha -4cos 2,alpha +3}{cos 4alpha +4cos 2,alpha +3}},}

operatorname{tg}^4,alpha = frac{cos 4alpha - 4cos 2,alpha + 3}{cos 4alpha + 4cos 2,alpha + 3},

ctg4α=cos⁡4α+4cos⁡2α+3cos⁡4α−4cos⁡2α+3.{displaystyle operatorname {ctg} ^{4},alpha ={frac {cos 4alpha +4cos 2,alpha +3}{cos 4alpha -4cos 2,alpha +3}}.}

operatorname{ctg}^4,alpha = frac{cos 4alpha + 4cos 2,alpha + 3}{cos 4alpha - 4cos 2,alpha + 3}.

Иллюстрация равенства sin⁡x−cos⁡x=2⋅sin⁡(x−π4){displaystyle sin x-cos x={sqrt {2}}cdot sin left(x-{pi over 4}right)} ${displaystyle sin x-cos x={sqrt {2}}cdot sin left(x-{pi over 4}right)}$

Суммы

sin⁡α±sin⁡β=2sin⁡α±β2cos⁡α∓β2,{displaystyle sin alpha pm sin beta =2sin {frac {alpha pm beta }{2}}cos {frac {alpha mp beta }{2}},}

{displaystyle sin alpha pm sin beta =2sin {frac {alpha pm beta }{2}}cos {frac {alpha mp beta }{2}},}

cos⁡α+cos⁡β=2cos⁡α+β2cos⁡α−β2,{displaystyle cos alpha +cos beta =2cos {frac {alpha +beta }{2}}cos {frac {alpha -beta }{2}},}

{displaystyle cos alpha +cos beta =2cos {frac {alpha +b eta }{2}}cos {frac {alpha -beta }{2}},}

cos⁡α−cos⁡β=−2sin⁡α+β2sin⁡α−β2,{displaystyle cos alpha -cos beta =-2sin {frac {alpha +beta }{2}}sin {frac {alpha -beta }{2}},}

{displaystyle cos alpha -cos beta =-2sin {frac {alpha +beta }{2}}sin {frac {alpha -beta }{2}},}

tg⁡α±tg⁡β=sin⁡(α±β)cos⁡αcos⁡β,{displaystyle operatorname {tg} alpha pm operatorname {tg} beta ={frac {sin(alpha pm beta )}{cos alpha cos beta }},}

{displaystyle operatorname {tg} alpha pm operatorname {tg} beta ={frac {sin(alpha pm beta )}{cos alpha cos beta }},}

ctg⁡α±ctg⁡β=sin⁡(β±α)sin⁡αsin⁡β,{displaystyle operatorname {ctg} alpha pm operatorname {ctg} beta ={frac {sin(beta pm alpha )}{sin alpha sin beta }},}

{displaystyle operatorname {ctg} alpha pm operatorname {ctg} beta ={frac {sin(beta pm alpha )}{sin alpha sin beta }},}

1±sin⁡2α=(sin⁡α±cos⁡α)2,{displaystyle 1pm sin {2alpha }=(sin alpha pm cos alpha )^{2},}

{displaystyle 1pm sin {2alpha }=(sin alpha pm cos alpha )^{2},}

sin⁡α±cos⁡α=2⋅sin⁡(α±π4).{displaystyle sin alpha pm cos alpha ={sqrt {2}}cdot sin left(alpha pm {pi over 4}right).}

{displaystyle sin alpha pm cos alpha ={sqrt {2}}cdot sin left(alpha pm {pi over 4}right).}

Существует представление:

Asin⁡α+Bcos⁡α=A2+B2sin⁡(α+ϕ),{displaystyle Asin alpha +Bcos alpha ={sqrt {A^{2}+B^{2}}};sin(alpha +phi ),}

Asin alpha +Bcos alpha ={sqrt {A^{2}+B^{2}}};sin(alpha +phi ),

где угол ϕ{displaystyle phi }

$phi$ находится из соотношений:

sin⁡ϕ=BA2+B2,{displaystyle sin phi ={frac {B}{sqrt {A^{2}+B^{2}}}},}

{displaystyle sin phi ={frac {B}{sqrt {A^{2}+B^{2}}}},}

cos⁡ϕ=AA2+B2.{displaystyle cos phi ={frac {A}{sqrt {A^{2}+B^{2}}}}.}

{displaystyle cos phi ={frac {A}{sqrt {A^{2}+B^{2}}}}.}

Универсальная тригонометрическая подстановка

Основная статья: Универсальная тригонометрическая подстановка

Все тригонометрические функции можно выразить через тангенс половинного угла:

sin⁡x=sin⁡x1=2sin⁡x2cos⁡x2sin2⁡x2+cos2⁡x2=2tg⁡x21+tg2⁡x2,{displaystyle sin x={frac {sin x}{1}}={frac {2sin {frac {x}{2}}cos {frac {x}{2}}}{sin ^{2}{frac {x}{2}}+cos ^{2}{frac {x}{2}}}}={frac {2operatorname {tg} {frac {x}{2}}}{1+operatorname {tg} ^{2}{frac {x}{2}}}},}

${displaystyle sin x={frac {sin x}{1}}={frac {2sin {frac {x}{2}}cos {frac {x}{2}}}{sin ^{2}{frac {x}{2}}+cos ^{2}{frac {x}{2}}}}={frac {2operatorname {tg} {frac {x}{2}}}{1+operatorname {tg} ^{2}{frac {x}{2}}}},}$

cos⁡x=cos⁡x1=cos2⁡x2−sin2⁡x2cos2⁡x2+sin2⁡x2=1−tg2⁡x21+tg2⁡x2,{displaystyle cos x={frac {cos x}{1}}={frac {cos ^{2}{frac {x}{2}}-sin ^{2}{frac {x}{2}}}{cos ^{2}{frac {x}{2}}+sin ^{2}{frac {x}{2}}}}={frac {1-operatorname {tg} ^{2}{frac {x}{2}}}{1+operatorname {tg} ^{2}{frac {x}{2}}}},}

${displaystyle cos x={frac {cos x}{1}}={frac {cos ^{2}{frac {x}{2}}-sin ^{2}{frac {x}{2}}}{cos ^{2}{frac {x}{2}}+sin ^{2}{frac {x}{2}}}}={frac {1-operatorname {tg} ^{2}{frac {x}{2}}}{1+operatorname {tg} ^{2}{frac {x}{2}}}},}$

tg⁡ x=sin⁡xcos⁡x=2tg⁡x21−tg2⁡x2,{displaystyle operatorname {tg} ~x={frac {sin x}{cos x}}={frac {2operatorname {tg} {frac {x}{2}}}{1-operatorname {tg} ^{2}{frac {x}{2}}}},}

${displaystyle operatorname {tg} ~x={frac {sin x}{cos x}}={frac {2operatorname {tg} {frac {x}{2}}}{1-operatorname {tg} ^{2}{frac {x}{2}}}},}$

ctg⁡ x=cos⁡xsin⁡x=1−tg2⁡x22tg⁡x2,{displaystyle operatorname {ctg} ~x={frac {cos x}{sin x}}={frac {1-operatorname {tg} ^{2}{frac {x}{2}}}{2operatorname {tg} {frac {x}{2}}}},}

${displaystyle operatorname {ctg} ~x={frac {cos x}{sin x}}={frac {1-operatorname {tg} ^{2}{frac {x}{2}}}{2operatorname {tg} {frac {x}{2}}}},}$

sec⁡x=1cos⁡x=1+tg2⁡x21−tg2⁡x2,{displaystyle sec x={frac {1}{cos x}}={frac {1+operatorname {tg} ^{2}{frac {x}{2}}}{1-operatorname {tg} ^{2}{frac {x}{2}}}},}

${displaystyle sec x={frac {1}{cos x}}={frac {1+operatorname {tg} ^{2}{frac {x}{2}}}{1-operatorname {tg} ^{2}{frac {x}{2}}}},}$

cosec⁡ x=1sin⁡x=1+tg2⁡x22tg⁡x2.{displaystyle operatorname {cosec} ~x={frac {1}{sin x}}={frac {1+operatorname {tg} ^{2}{frac {x}{2}}}{2operator
name {tg} {frac {x}{2}}}}.}

${displaystyle operatorname {cosec} ~x={frac {1}{sin x}}={frac {1+operatorname {tg} ^{2}{frac {x}{2}}}{2operatorname {tg} {frac {x}{2}}}}.}$

Исследование функций в математическом анализе

Разложение в бесконечные произведения

Тригонометрические функции могут быть представлены в виде бесконечного произведения многочленов:

sin⁡x=x∏n=1∞(1−x2π2n2),{displaystyle sin x=x,prod _{n=1}^{infty }left(1-{frac {x^{2}}{pi ^{2}n^{2}}}right),}

{displaystyle sin x=x,prod _{n=1}^{infty }left(1-{frac {x^{2}}{pi ^{2}n^{2}}}right),}

cos⁡x=∏n=0∞(1−4×2π2(2n+1)2).{displaystyle cos x=prod _{n=0}^{infty }left(1-{frac {4x^{2}}{pi ^{2}(2n+1)^{2}}}right).}

{displaystyle cos x=prod _{n=0}^{infty }left(1-{frac {4x^{2}}{pi ^{2}(2n+1)^{2}}}right).}

Эти соотношения выполняются при любом значении x{displaystyle x}

$x$ .

Непрерывные дроби

Разложение тангенса в непрерывную дробь:

tg⁡x=x1−x23−x25−x27−x2⋱{displaystyle mathop {rm {tg}} x={frac {x}{1-{frac {x^{2}}{3-{frac {x^{2}}{5-{frac {x^{2}}{7-{frac {x^{2}}{ddots }}}}}}}}}}}

{displaystyle mathop {rm {tg}} x={frac {x}{1-{frac {x^{2}}{3-{frac {x^{2}}{5-{frac {x^{2}}{7-{frac {x^{2}}{ddots }}}}}}}}}}}

Производные и первообразные

Все тригонометрические функции непрерывно и неограниченно дифференцируемы на всей области определения:

(sin⁡x)′=cos⁡x,{displaystyle (sin x)’=cos x,,}

$( sin x )' = cos x ,,$

(cos⁡x)′=−sin⁡x,{displaystyle (cos x)’=-sin x,,}

$( cos x )' = -sin x ,,$

(tg⁡x)′=1cos2⁡x=1+tg2⁡x=sec2⁡x,{displaystyle (operatorname {tg} x)’={frac {1}{cos ^{2}x}}=1+operatorname {tg} ^{2}x=sec ^{2}x,}

${displaystyle (operatorname {tg} x)'={frac {1}{cos ^{2}x}}=1+operatorname {tg} ^{2}x=sec ^{2}x,}$

(ctg⁡x)′=−1sin2⁡x=−cosec2⁡x,{displaystyle (operatorname {ctg} x)’=-{frac {1}{sin ^{2}x}}=-operatorname {cosec} ^{2}x,}

${displaystyle (operatorname {ctg} x)'=-{frac {1}{sin ^{2}x}}=-operatorname {cosec} ^{2}x,}$

(sec⁡x)′=sin⁡xcos2⁡x=sec⁡xtg⁡x,{displaystyle (sec x)’={frac {sin x}{cos ^{2}x}}=sec xoperatorname {tg} x,}

${displaystyle (sec x)'={frac {sin x}{cos ^{2}x}}=sec xoperatorname {tg} x,}$

(cosec⁡ x)′=−cos⁡xsin2⁡x.{displaystyle (operatorname {cosec} ~x)’=-{frac {cos x}{sin ^{2}x}}.}

$( operatorname{cosec}~x)' = -frac{cos x}{sin ^2 x}.$

Интегралы тригонометрических функций на области определения выражаются через элементарные функции следующим образ?