Симметризация Штайнера

Разделы:
- Круговой симметризации

Эту страницу в данный момент активно редактирует участник Тоша (обс.) 14:20, 7 июля 2018 (UTC).Пожалуйста, не вносите в неё никаких изменений до тех пор, пока не исчезнет это объявление.
В противном случае могут возникнуть конфликты редактирования.
Объявление размещено Тоша (обс.) 14:20, 7 июля 2018 (UTC) и не должно присутствовать на странице более двух суток. Для автоматического указания даты установки предупреждения используйте конструкцию .ts-templateCallCode-weak:first-child>.ts-templateCallCode-pipe:first-child{margin-left:0}.mw-parser-output .ts-templateCallCode-param+.ts-templateCallCode-closing{margin-left:2px}.mw-parser-output span.ts-templateCallCode>.ts-templateCallCode-templateName a{padding:0 0.5em!important;position:relative;margin:-0.5em}]]>{{subst:L}}

[[Категория:Википедия:Ошибка выражения: неожидаемый оператор <, редактируемые прямо сейчас]]

Симметризация Штейнера — построение определённого типа, дающее фигуру с зеркальноой симмтрией из произвольной фигуры.Это построение применяется при решении изопериметрической задачи,предложеном Якобом Штайнером в 1838.

На основе симметризации Штейнера были построены и другие симметризации, которые используются в схожих задачах.

Содержание

Симметризации штейнера

Симметризация Штейнера фигуры

Пусть H⊂Rn{displaystyle Hsubset mathbb {R} ^{n}}

${displaystyle Hsubset mathbb {R} ^{n}}$ есть гиперплоскость и Φ{displaystyle Phi } $Phi$ — данная фигура.

Введём ортогональную систему координат в которой H{displaystyle H}

$H$ описывается уравнением xn=0{displaystyle x_{n}=0} ${displaystyle x_{n}=0}$ .Для каждого x∈H{displaystyle xin H} $xin H$ , пусть ℓx{displaystyle ell _{x}} ${displaystyle ell _{x}}$ обозначает длину пересечения перпендикуляра к H{displaystyle H} ${displaystyle H}$ через x{displaystyle x} $x$ с множеством Φ{displaystyle Phi } $Phi$ .Далее проведём через x{displaystyle x} $x$ длины ℓx{displaystyle ell _{x}} ${displaystyle ell _{x}}$ с серединой в x{displaystyle x} $x$ и перпендикулярный к H{displaystyle H} $H$ .Объединение Φ∗{displaystyle Phi ^{*}} ${displaystyle Phi ^{*}}$ таких отрезков есть симметризация Штейнера Φ{displaystyle Phi } $Phi$ относительно H{displaystyle H} $H$ .

Свойства

Объём Φ∗{displaystyle Phi ^{*}} ${displaystyle Phi ^{*}}$ совпадает с объёмом Φ{displaystyle Phi } $Phi$ .
Площадь поверхности Φ∗{displaystyle Phi ^{*}} ${displaystyle Phi ^{*}}$ не превосходит площади поверхности Φ{displaystyle Phi } $Phi$ .
Если Φ{displaystyle Phi } $Phi$ выпукла, то то же верно и для Φ∗{displaystyle Phi ^{*}} ${displaystyle Phi ^{*}}$ .
Симметризация Штейнера не увеличивает расстояние по Хаусдорфу между фигурами, то есть

dH(Φ,Ψ)≥dH(Φ∗,Ψ∗),{displaystyle d_{H}(Phi ,Psi )geq d_{H}(Phi ^{*},Psi ^{*}),} ${displaystyle d_{H}(Phi ,Psi )geq d_{H}(Phi ^{*},Psi ^{*}),}$

где Φ{displaystyle Phi }

Phi

и Ψ{displaystyle Psi }

Psi

— произвольные фигуры, Φ∗{displaystyle Phi ^{*}}

{displaystyle Phi ^{*}}

и Ψ∗{displaystyle Psi ^{*}}

{displaystyle Psi ^{*}}

— их симметризации относительно гиперплоскости H{displaystyle H}

H

, а dH{displaystyle d_{H}}

{displaystyle d_{H}}

— метрика Хаусдорфа.

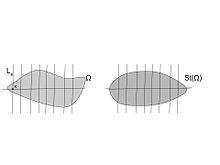
Круговой симметризации

Круговой симметризации набор Омега

Популярный метод симметризации в плоскости круговой симметризации Полья,. После ее обобщения будут описаны в высших измерениях. Давайте {displaystyle } ${displaystyle }$ быть домена; затем его круговой симметризации {displaystyle } ${displaystyle }$ с учетом положительной вещественной оси определяется следующим образом: пусть

В высших измерениях {displaystyle } ${displaystyle }$ его сферическая симметризация {displaystyle } ${displaystyle }$ в зависимости от положительной оси {displaystyle } ${displaystyle }$ определяется следующим образом: пусть{displaystyle } ${displaystyle }$ т. е. содержать крышки радиусом R, содержащиеся в {displaystyle } ${displaystyle }$ . Кроме того, для первой координаты давайте {displaystyle } ${displaystyle }$ если {displaystyle } ${displaystyle }$ . Так же как и выше

If Ωr{displaystyle Omega _{r}} ${displaystyle Omega _{r}}$ is the full cap, then Spn(Ω)∩{|z|=r}:={|z|=r}{displaystyle Sp^{n}(Omega )cap {|z|=r}:={|z|=r}} ${displaystyle Sp^{n}(Omega )cap {|z|=r}:={|z|=r}}$ .
If the surface area is ms(Ωt)=α{displaystyle m_{s}(Omega _{t})=alpha } ${displaystyle m_{s}(Omega _{t})=alpha }$ , then Spn(Ω)∩{|z|=r}:={x:|x|=r{displaystyle Sp^{n}(Omega )cap {|z|=r}:={x:|x|=r} ${displaystyle Sp^{n}(Omega )cap {|z|=r}:={x:|x|=r}$ and 0≤angle⁡(x1)≤θα}=:C(θα){displaystyle 0leq operatorname {angle} (x_{1})leq theta _{alpha }}=:C(theta _{alpha })} ${displaystyle 0leq operatorname {angle} (x_{1})leq theta _{alpha }}=:C(theta _{alpha })}$ where θα{displaystyle theta _{alpha }} ${displaystyle theta _{alpha }}$ is picked so that its surface area is ms(C(θα)=α{displaystyle m_{s}(C(theta _{alpha })=alpha } ${displaystyle m_{s}(C(theta _{alpha })=alpha }$ . In words, C(θα){displaystyle C(theta _{alpha })} ${displaystyle C(theta _{alpha })}$ is a cap symmetric around the positive axis x1{displaystyle x_{1}} $x_{1}$ with the same area as the intersection Ω∩{|z|=r}{displaystyle Omega cap {|z|=r}} ${displaystyle Omega cap {|z|=r}}$ .
0,∞∈Spn(Ω){displaystyle 0,infty in Sp^{n}(Omega )} ${displaystyle 0,infty in Sp^{n}(Omega )}$ iff 0,∞∈Ω{displaystyle 0,infty in Omega } ${displaystyle 0,infty in Omega }$ .

Давайте {displaystyle } ${displaystyle }$ быть домен и {displaystyle } ${displaystyle }$ быть гиперплоскости, проходящей через начало координат. Обозначим отражения на самолет в положительное полупространство {displaystyle } ${displaystyle }$ как {displaystyle } ${displaystyle }$ или просто {displaystyle } ${displaystyle }$ когда это ясно из контекста. Кроме того, отраженных {displaystyle } ${displaystyle }$ по гиперплоскости х определяется как {displaystyle } ${displaystyle }$ . Затем, поляризованных {displaystyle } ${displaystyle }$ обозначается как {displaystyle } ${displaystyle }$ и определяется следующим образом

Если {displaystyle } ${displaystyle }$ тогда {displaystyle } ${displaystyle }$ .
Если {displaystyle } ${displaystyle }$ тогда {displaystyle } ${displaystyle }$ .
Если {displaystyle } ${displaystyle }$ тогда {displaystyle } ${displaystyle }$ .

В словах, {displaystyle } ${displaystyle }$ просто погрузитесь в полупространство {displaystyle } ${displaystyle }$ . Получается, что эта трансформация может аппроксимировать выше (в Хаусдорфа расстояние) (см. Brock & Solynin (2000)).