Радиа́н (русское обозначение: рад, международное: rad; от лат. radius — луч, радиус) — угол, соответствующий дуге, длина которой равна её радиусу[1]. Единица измерения плоских углов в Международной системе единиц (СИ), а также в системах единиц СГС и МКГСС[2].
 1 радиан — центральный угол, длина дуги которого равна радиусу окружности.
1 радиан — центральный угол, длина дуги которого равна радиусу окружности.
Радианная мера — угловая мера, в которой за единицу принимается угол в 1 радиан. То есть, радианная мера любого угла — это отношение этого угла к радиану[3]. Из определения следует, что величина полного угла равна 2π радиан (см. рис. справа).
Определить радианную меру можно и так: радианная мера угла — отношение длины дуги окружности, находящейся между сторонами угла, к радиусу этой окружности, когда центр окружности совпадает с вершиной угла. В геометрии для определения радианной меры угла используют единичную окружность с центром в вершине угла; тогда радианная мера угла равна длине дуги единичной окружности между сторонами угла[4][5].
Поскольку длина дуги окружности пропорциональна её угловой мере и радиусу, длина дуги окружности радиуса R и угловой величины α, измеренной в радианах, равна α ∙ R.
Так как величина угла, выраженная в радианах, равна отношению длины дуги окружности (м) к длине её радиуса (м), угол в радианном измерении — величина безразмерная.
Содержание
- 1 Радиан в Международной системе единиц (СИ)
- 2 Связь радиана с другими единицами
- 3 Радианная мера в математическом анализе
- 4 История
- 5 См. также
- 6 Примечания
- 7 Литература
Радиан в Международной системе единиц (СИ)
В качестве единицы измерения плоских углов в Международной системе единиц (СИ) радиан был принят XI Генеральной конференцией по мерам и весам в 1960 году одновременно с принятием системы СИ в целом[6]. В настоящее время в системе СИ радиан квалифицируется как когерентная[7] безразмерная производная единица СИ, имеющая специальные наименование и обозначение. Русское обозначение — рад, международное — rad[8].
Безразмерность плоского угла означает, что единицей его измерения является число один. Однако, применительно к плоскому углу единице «один» было присвоено специальное наименование «радиан» для того, чтобы в каждом конкретном случае облегчить понимание того, какая именно величина имеется в виду[9].
Кратные и дольные единицы
Десятичные кратные и дольные единицы радиана образуются с помощью стандартных приставок СИ, однако используются редко. Так, в миллирадианах, микрорадианах и нанорадианах измеряется угловое разрешение в астрономии. В кратных единицах (килорадианах и т. д.) измеряетсянабег угловой фазы. Сокращённое обозначение (рад, rad) основной и производных единиц не следует путать с устаревшей единицей измерения поглощённой дозы ионизирующего излучения — рад.
| Кратные | Дольные | ||||||
|---|---|---|---|---|---|---|---|
| величина | название | обозначение | величина | название | обозначение | ||
| 101 рад | декарадиан | дарад | darad | 10−1 рад | децирадиан | драд | drad |
| 102 рад | гекторадиан | град | hrad | 10−2 рад | сантирадиан | срад | crad |
| 103 рад | килорадиан | крад | krad | 10−3 рад | миллирадиан | мрад | mrad |
| 106 рад | мегарадиан | Мрад | Mrad | 10−6 рад | микрорадиан | мкрад | µrad |
| 109 рад | гигарадиан | Град | Grad | 10−9 рад | нанорадиан | нрад | nrad |
| 1012 рад | терарадиан | Трад | Trad | 10−12 рад | пикорадиан | прад | prad |
| 1015 рад | петарадиан | Прад | Prad | 10−15 рад | фемторадиан | фрад | frad |
| 1018 рад | эксарадиан | Эрад | Erad | 10−18 рад | атторадиан | арад | arad |
| 1021 рад | зеттарадиан | Зрад | Zrad | 10−21 рад | зепторадиан | зрад | zrad |
| 1024 рад | иоттарадиан | Ирад | Yrad | 10−24 рад | иокторадиан | ирад | yrad |
| 1027 рад | роннарадиан | Ррад | Rrad | 10−27 рад | ронторадиан | ррад | rrad |
| 1030 рад | кветтарадиан | Кврад | Qrad | 10−30 рад | квекторадиан | кврад | qrad |
| рекомендовано к применению применять не рекомендуется не применяются или редко применяются на практике | |||||||
Связь радиана с другими единицами
Пропорциональное соотношение радиана с другими единицами измерения углов описывается формулой:
Очевидно, развернутый угол равен 180∘,{displaystyle 180^{circ },}
или π⋅rr=π{displaystyle {frac {pi cdot r}{r}}=pi } радианам. Отсюда вытекает тривиальная формула пересчёта из градусов, минут и секунд в радианы и наоборот.
- a[°] = α[рад] × (360° / (2π)) или α[рад] × (180° / π),
- α[рад] = a[°] : (180° / π) = a[°] × (π / 180°),
где α[рад] — угол в радианах, a[°] — угол в градусах.
1 рад (или p∘{displaystyle p^{circ }}
) = 360∘2π≈57,295779513∘≈57∘17′44,806″{displaystyle {frac {360^{circ }}{2pi }}approx 57{,}295779513^{circ }approx 57^{circ }17’44{,}806»} (мнемоническое правило запоминания в градусах-минутах-секундах: «Число радиана и порядок шутя пишу наизусть», где число букв в каждом слове равно соответствующей цифре в записи значения радиана, до десятой доли угловой секунды)
p′{displaystyle p’}
(или 1 рад в минутах) = 360∘⋅60′2π≈3437,747′{displaystyle {frac {360^{circ }cdot 60′}{2pi }}approx 3437{,}747′}
p″{displaystyle p»}
(или 1 рад в секундах) = 360∘⋅60′⋅60″2π≈206264,8″.{displaystyle {frac {360^{circ }cdot 60’cdot 60»}{2pi }}approx 206264{,}8».}  Номограмма для перевода радианы/градусы.
Номограмма для перевода радианы/градусы.
В метрической системе угловых мер прямой угол делится на 100 градов и каждый град на 100 сантиградов, который, в свою очередь, делится на сотые доли сантиграда, так что
p‵‵{displaystyle p^{backprime backprime }}
(или 1 рад в сотых долях «сантиграда») = 400⋅100⋅1002π=636620.{displaystyle {frac {400cdot 100cdot 100}{2pi }}=636620.}
Употреблять его практически не приходится, так как метрическая система угловых мер пока не получила широкого распространения.
Чтобы легче запомнить, как переводят радианы в градусы и обратно, заметим:
Переводя радианы в градусы (или в минуты, или в секунды), мы из отвлеченного числа (rad{displaystyle mathrm {rad} }
) делаем именованное (p∘,p′,p″{displaystyle p^{circ },p’,p»} ) и поэтому должны множить на p∘ ({displaystyle p^{circ }~(} или p′,p″){displaystyle p’,p»)} ;
Переводя градусы в радианы, мы, наоборот, уничтожаем наименование: получаем отвлечённое число; значит, здесь надо делить на p∘ ({displaystyle p^{circ }~(} или p′,p″),{displaystyle p’,p»),} либо же умножать на перевёрнутуюдробь 1p∘ (1p′,1p″).{displaystyle {frac {1}{p^{circ }}}~({frac {1}{p’}},{frac {1}{p»}}).}
Пример 1. Перевести в радианы 5∘43′46″.{displaystyle 5^{circ }43’46».}
α[rad]≖5∘=5∘p∘ rad=0,08726{displaystyle {boldsymbol {alpha }}[mathrm {rad} ]eqcirc 5^{circ }={frac {5^{circ }}{displaystyle {p^{circ }}}}~mathrm {rad} =0{,}0872_{6}}
43′=43′p′ rad=0,012508{displaystyle 43’={frac {43′}{p’}}~mathrm {rad} =0{,}0125_{08}}
46″=46″p″ rad=0,000223{displaystyle 46»={frac {46»}{p»}}~mathrm {rad} =0{,}0002_{23}}
∑≈0,09999 rad{displaystyle sum approx 0{,}0999_{9}~mathrm {rad} }
[10]=0,1 rad{displaystyle =0{,}1~mathrm {rad} }
Альтернативный способ предусматривает перевод минут и секунд в десятичные (сотые и десятитысячные) доли градуса,
и однократного деления на p∘:{displaystyle p^{circ }:}
(как правило, этот способ более точен)
46″=46″60″=0,77′{displaystyle 46»={frac {46»}{60»}}=0{,}{boldsymbol {77}}’}
43,77′=43,77′60′=0,7295∘{displaystyle 43{,}{boldsymbol {77}}’={frac {43{,}77′}{60′}}=0{,}{boldsymbol {7295}}^{circ }}
∑=5,7295∘{displaystyle sum =5{,}{boldsymbol {7295}}^{circ }}
5,7295∘=5,7295∘p∘ rad=5,7295∘57,295∘=0,1 rad{displaystyle 5{,}7295^{circ }={frac {5{,}7295^{circ }}{p^{circ }}}~mathrm {rad} ={frac {5{,}7295^{circ }}{displaystyle {57{,}295^{circ }}}}=0{,}1~mathrm {rad} }
Пример 2. Перевести в градусы 1 радиан.
a[∘]≖1⋅360∘2π=1⋅57,29578∘=57,29578∘{displaystyle a[^{circ }]eqcirc 1cdot {frac {360^{circ }}{2pi }}=1cdot 57{,}29578^{circ }=57{,}{boldsymbol {29578}}^{circ }}
0,29578∘⋅60′=17,7468′{displaystyle 0{,}{boldsymbol {29578}}^{circ }cdot 60’=17{,}{boldsymbol {7468}}’}
0,7468′⋅60″=44,807″≈45″{displaystyle 0{,}{boldsymbol {7468}}’cdot 60»=44{,}807»approx 45»}
Итого ≈57∘17′45″.{displaystyle approx 57^{circ }17’45».}
Радианная мера в математическом анализе
При рассмотрении тригонометрических функций в математическом анализе всегда считается, что аргумент выражен в радианах, что упрощает запись; при этом само обозначение рад (rad) часто опускается.
При малых углах синус и тангенс угла, выраженного в радианах, приблизительно равны самому углу (в радианах), что удобно при приближённых вычислениях. При углах менее 0,1 rad (5∘43′,77){displaystyle 0{,}1~mathrm {rad} ~(5^{circ }43′{,}77)}
, приближение можно считать верным до третьего знака после запятой. Если угол меньше 0,01 rad (0∘34′,38){displaystyle 0{,}01~mathrm {rad} ~(0^{circ }34′{,}38)} , — то до шестого знака после запятой[11]:
- sinα≈tgα≈α.{displaystyle sin alpha approx operatorname {tg} ,alpha approx alpha .}
История
Первое использование радиана вместо углового градуса обычно приписывают Роджеру Котсу (XVIII век), который считал эту единицу измерения угла н
аиболее естественной[12]. Однако идея измерять длину дуги радиусом окружности использовалась и другими математиками. Например, Аль-Каши использовал единицу измерения, названную им «часть диаметра», которая равнялась 1/60 радиана. Также им использовались и более мелкие производные единицы[13].
Термин «радиан» впервые появился в печати 5 июня 1873 года в экзаменационных билетах, составленных Джеймсом Томсоном из Университета Квинса в Белфасте. Томсон использовал термин не позднее 1871 года, в то время как Томас Мьюр из Сент-Эндрюсского университета в 1869 году колебался в выборе между терминами «рад», «радиал» и «радиан». В 1874 году Мьюр, после консультаций с Джеймсом Томсоном, решил использовать термин «радиан»[14][15][16].
См. также
- Град, минута, секунда
- Градус, минута, секунда
- Оборот (единица измерения)
- Парсек
- Стерадиан
- Тысячная (угол)
Примечания
- ↑ Радиан // Математическая энциклопедия (в 5 томах). — М.: Советская Энциклопедия, 1984. — Т. 4.
- ↑ Деньгуб В. М., Смирнов В. Г. Единицы величин. Словарь-справочник. — М.: Издательство стандартов, 1990. — С. 98. — 240 с. — ISBN 5-7050-0118-5.
- ↑ Выгодский, 1965.
- ↑ Гельфанд, Львовский, Тоом, 2002.
- ↑ David E. Joyce. Measurement of Angles (англ.). Dave’s Short Trig Course. Clark University. Дата обращения: 8 сентября 2015.
- ↑ Резолюция 12 XI Генеральной конференции по мерам и весам (1960) (англ.). Международное бюро мер и весов. Дата обращения: 19 декабря 2014.
- ↑ Производная единица измерения называется когерентной, если она выражается в виде произведения степеней основных единиц измерения с коэффициентом пропорциональности, равным единице.
- ↑ ГОСТ 8.417-2002. Государственная система обеспечения единства измерений. Единицы величин. (неопр.) Дата обращения: 18 сентября 2012. Архивировано из оригинала 10 ноября 2012 года.
- ↑ Units for dimensionless quantities, also called quantities of dimension one (англ.). SI Brochure: The International System of Units (SI). Международное бюро мер и весов (2006). Дата обращения: 19 декабря 2014.
- ↑ 1 2 3 4 Лишние цифры [после четвёртого знака после запятой] в выражениях минут и секунд зачастую отбрасываются ввиду того, что следующая цифра в выражении градусов неизвестна, и, следовательно, писать цифры дальше четвёртой [обозначены нижним индексом] — напрасный труд.
- ↑ sin5∘43′,77=0,0998≈0,100{displaystyle sin 5^{circ }43′{,}77=0{,}0998approx 0{,}100}
- tg5∘43′,77=0,1003≈0,100{displaystyle operatorname {tg} 5^{circ }43′{,}77=0{,}1003approx 0{,}100} (точность нарушается в четвертом знаке после запятой)
- sin0∘34′,38=0,0099998≈0,010000{displaystyle sin 0^{circ }34′{,}38=0{,}0099998approx 0{,}010000}
- tg0∘34′,38=0,0100003≈0,010000{displaystyle operatorname {tg} 0^{circ }34′{,}38=0{,}0100003approx 0{,}010000} (точность не выдерживается в седьмом знаке после запятой)
Именно поэтому промежутки шкал(ы) на счётной линейке имеют пределы 5∘43′,77 (≈5∘43′46″){displaystyle 5^{circ }43′{,}77~(approx 5^{circ }43’46»)} и 0∘34′,38 (≈0∘34′23″){displaystyle 0^{circ }34′{,}38~(approx 0^{circ }34’23»)} ; ниже этого значения (до 0) разграфки нет, так как углы (в радианах) совпадают со значениями синусов/тангенсов в пределах точности линейки (Панов Д. Ю. Счётная линейка. — 25-е изд. — М.: изд-во Наука (Гл. ред. физ.-мат. литературы), 1982. — 176 с.)
- ↑ O’Connor, J. J.; Robertson, E. F. Biography of Roger Cotes (неопр.). The MacTutor History of Mathematics (февраль 2005).
- ↑ Luckey, Paul. Der Lehrbrief über den kreisumfang von Gamshid b. Mas’ud al-Kasi (нем.) / Siggel, A.. — Berlin: Akademie Verlag, 1953. — S. 40.
- ↑ Florian Cajori. History of Mathematical Notations (неопр.). — 1929. — Т. 2. — С. 147—148. — ISBN 0-486-67766-4.
- ↑ Muir, Thos. The Term «Radian» in Trigonometry (англ.) // Nature. — 1910. — Vol. 83, no. 2110. — P. 156. — doi:10.1038/083156a0. — Bibcode: 1910Natur..83..156M.Thomson, James. The Term «Radian» in Trigonometry (англ.) // Nature. — 1910. — Vol. 83, no. 2112. — P. 217. — doi:10.1038/083217c0. — Bibcode: 1910Natur..83..217T.Muir, Thos. The Term «Radian» in Trigonometry (англ.) // Nature. — 1910. — Vol. 83, no. 2120. — P. 459—460. — doi:10.1038/083459d0. — Bibcode: 1910Natur..83..459M.
- ↑ Miller, Jeff Earliest Known Uses of Some of the Words of Mathematics (неопр.) (23 ноября 2009). Дата обращения: 30 сентября 2011.
Литература
- Выгодский М. Я. Справочник по элементарной математике. — Наука, 1965. — С. 340—343. — 424 с.
- Гельфанд И. М., Львовский С. М., Тоом А. Л. Тригонометрия. — М.: МЦНМО, 2002. — С. 7—8. — 199 с. — ISBN 5-94057-050-X.
| В другом языковом разделе есть более полная статья Radian (англ.). Вы можете помочь проекту, расширив текущую статью с помощью перевода |

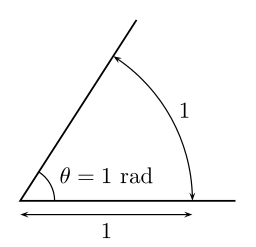
 или π⋅rr=π{displaystyle {frac {pi cdot r}{r}}=pi }
или π⋅rr=π{displaystyle {frac {pi cdot r}{r}}=pi } радианам. Отсюда вытекает тривиальная формула пересчёта из
радианам. Отсюда вытекает тривиальная формула пересчёта из  ) = 360∘2π≈57,295779513∘≈57∘17′44,806″{displaystyle {frac {360^{circ }}{2pi }}approx 57{,}295779513^{circ }approx 57^{circ }17’44{,}806»}
) = 360∘2π≈57,295779513∘≈57∘17′44,806″{displaystyle {frac {360^{circ }}{2pi }}approx 57{,}295779513^{circ }approx 57^{circ }17’44{,}806»} (мнемоническое правило запоминания в градусах-минутах-секундах: «Число радиана и порядок шутя пишу наизусть», где число букв в каждом слове равно соответствующей цифре в записи значения радиана, до десятой доли угловой секунды)
(мнемоническое правило запоминания в градусах-минутах-секундах: «Число радиана и порядок шутя пишу наизусть», где число букв в каждом слове равно соответствующей цифре в записи значения радиана, до десятой доли угловой секунды) (или 1 рад в минутах) = 360∘⋅60′2π≈3437,747′{displaystyle {frac {360^{circ }cdot 60′}{2pi }}approx 3437{,}747′}
(или 1 рад в минутах) = 360∘⋅60′2π≈3437,747′{displaystyle {frac {360^{circ }cdot 60′}{2pi }}approx 3437{,}747′}
 (или 1 рад в секундах) = 360∘⋅60′⋅60″2π≈206264,8″.{displaystyle {frac {360^{circ }cdot 60’cdot 60»}{2pi }}approx 206264{,}8».}
(или 1 рад в секундах) = 360∘⋅60′⋅60″2π≈206264,8″.{displaystyle {frac {360^{circ }cdot 60’cdot 60»}{2pi }}approx 206264{,}8».}
 (или 1 рад в сотых долях «сантиграда») = 400⋅100⋅1002π=636620.{displaystyle {frac {400cdot 100cdot 100}{2pi }}=636620.}
(или 1 рад в сотых долях «сантиграда») = 400⋅100⋅1002π=636620.{displaystyle {frac {400cdot 100cdot 100}{2pi }}=636620.}
 ) делаем именованное (p∘,p′,p″{displaystyle p^{circ },p’,p»}
) делаем именованное (p∘,p′,p″{displaystyle p^{circ },p’,p»} ) и поэтому должны множить на p∘ ({displaystyle p^{circ }~(}
) и поэтому должны множить на p∘ ({displaystyle p^{circ }~(} или p′,p″){displaystyle p’,p»)}
или p′,p″){displaystyle p’,p»)} ;
; либо же умножать на перевёрнутуюдробь 1p∘ (1p′,1p″).{displaystyle {frac {1}{p^{circ }}}~({frac {1}{p’}},{frac {1}{p»}}).}
либо же умножать на перевёрнутуюдробь 1p∘ (1p′,1p″).{displaystyle {frac {1}{p^{circ }}}~({frac {1}{p’}},{frac {1}{p»}}).}

![{displaystyle {boldsymbol {alpha }}[mathrm {rad} ]eqcirc 5^{circ }={frac {5^{circ }}{displaystyle {p^{circ }}}}~mathrm {rad} =0{,}0872_{6}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/53b95203f66ade334f7459a20cc4aed34f8797fd)




 (как правило, этот способ более точен)
(как правило, этот способ более точен)



![a[^{circ }]eqcirc 1cdot {frac {360^{circ }}{2pi }}=1cdot 57{,}29578^{circ }=57{,}{boldsymbol {29578}}^{circ }](https://wikimedia.org/api/rest_v1/media/math/render/svg/f43329e10793951c24756957d3c38ae9481215c5)



 , приближение можно считать верным до третьего знака после запятой. Если угол меньше 0,01 rad (0∘34′,38){displaystyle 0{,}01~mathrm {rad} ~(0^{circ }34′{,}38)}
, приближение можно считать верным до третьего знака после запятой. Если угол меньше 0,01 rad (0∘34′,38){displaystyle 0{,}01~mathrm {rad} ~(0^{circ }34′{,}38)} , — то до шестого знака после запятой
, — то до шестого знака после запятой

 (точность нарушается в четвертом знаке после запятой)
(точность нарушается в четвертом знаке после запятой)
 (точность не выдерживается в седьмом знаке после запятой)
(точность не выдерживается в седьмом знаке после запятой) и 0∘34′,38 (≈0∘34′23″){displaystyle 0^{circ }34′{,}38~(approx 0^{circ }34’23»)}
и 0∘34′,38 (≈0∘34′23″){displaystyle 0^{circ }34′{,}38~(approx 0^{circ }34’23»)} ; ниже этого значения (до 0) разграфки нет, так как углы (в радианах) совпадают со значениями синусов/тангенсов в пределах точности линейки (Панов Д. Ю. Счётная линейка. — 25-е изд. — М.: изд-во Наука (Гл. ред. физ.-мат. литературы), 1982. — 176 с.)
; ниже этого значения (до 0) разграфки нет, так как углы (в радианах) совпадают со значениями синусов/тангенсов в пределах точности линейки (Панов Д. Ю. Счётная линейка. — 25-е изд. — М.: изд-во Наука (Гл. ред. физ.-мат. литературы), 1982. — 176 с.)