Правильный многоугольник

Разделы:

Пра́вильный многоуго́льник — это выпуклый многоугольник, у которого все стороны между собой равны и все углы между смежными сторонами равны.

Восьмиугольник
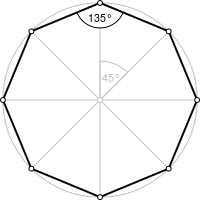Правильный восьмиугольник
Тип	Правильный многоугольник
Рёбра	8
Символ Шлефли	{8}, t{4}
Диаграмма Коксетера — Дынкина
Вид симметрии	Диэдрическая группа (D5)
Площадь	2cot⁡π8a2{displaystyle 2cot {frac {pi }{8}}a^{2}} ${displaystyle 2cot {frac {pi }{8}}a^{2}}$ =2(1+2)a2≃4.828a2.{displaystyle =2(1+{sqrt {2}})a^{2}simeq 4.828,a^{2}.} ${displaystyle =2(1+{sqrt {2}})a^{2}simeq 4.828,a^{2}.}$
Внутренний угол	135°
Свойства
выпуклый, вписанный, равносторонний, равноугольный [en], изотоксаль ный
Медиафайлы на Викискладе

Определение правильного многоугольника может зависеть от определения многоугольника: если он определён как плоская замкнутая ломаная, то появляется определение правильного звёздчатого многоугольника как невыпуклого многоугольника, у которого все стороны между собой равны и все углы между собой равны.

Содержание

1 Свойства
2 Применение
3 История
4 См. также
5 Примечания

Свойства

Координаты

Пусть xC{displaystyle x_{C}}

$x_{C}$ и yC{displaystyle y_{C}} $y_{C}$ — координаты центра, а R{displaystyle R} $R$ — радиус описанной вокруг правильного многоугольника окружности, ϕ0{displaystyle {phi }_{0}} ${phi }_{0}$ — угловая координата первой вершины, тогда декартовы координаты вершин правильного n-угольника определяются формулами:

xi=xC+Rcos⁡(ϕ0+2πin){displaystyle x_{i}=x_{C}+Rcos left({phi }_{0}+{frac {2pi i}{n}}right)}

x_{i}=x_{C}+Rcos left({phi }_{0}+{frac {2pi i}{n}}right)

yi=yC+Rsin⁡(ϕ0+2πin){displaystyle y_{i}=y_{C}+Rsin left({phi }_{0}+{frac {2pi i}{n}}right)}

y_{i}=y_{C}+Rsin left({phi }_{0}+{frac {2pi i}{n}}right)

где i=0…n−1{displaystyle i=0dots n-1}

$i=0dots n-1$

Размеры

Правильный многоугольник, вписанный и описанный около окружности

Пусть R{displaystyle R}

$R$ — радиус описанной вокруг правильного многоугольника окружности, тогда радиус вписанной окружности равен

r=Rcos⁡πn{displaystyle r=Rcos {frac {pi }{n}}}

r=Rcos {frac {pi }{n}}

а длина стороны многоугольника равна

a=2Rsin⁡πn=2rtgπn{displaystyle a=2Rsin {frac {pi }{n}}=2rmathop {mathrm {tg} } ,{frac {pi }{n}}}

a=2Rsin {frac {pi }{n}}=2r{mathop {{mathrm {tg}}}},{frac {pi }{n}}

Площадь

Площадь правильного многоугольника с числом сторон n{displaystyle n}

$n$ и длиной стороны a{displaystyle a} $a$ составляет:

S=n4 a2ctg⁡πn{displaystyle S={frac {n}{4}} a^{2}mathop {mathrm {} } ,operatorname {ctg} {frac {pi }{n}}}

S={frac {n}{4}} a^{2}{mathop {{mathrm {}}}},operatorname {ctg}{frac {pi }{n}}

Площадь правильного многоугольника с числом сторон n{displaystyle n}

$n$ , вписанного в окружность радиуса R{displaystyle R} $R$ , составляет:

S=n2R2sin⁡2πn{displaystyle S={frac {n}{2}}R^{2}sin {frac {2pi }{n}}}

S={frac {n}{2}}R^{2}sin {frac {2pi }{n}}

Площадь правильного многоугольника с числом сторон n{displaystyle n}

$n$ , описанного вокруг окружности радиуса r{displaystyle r} $r$ , составляет:

S=nr2tgπn{displaystyle S=nr^{2}mathop {mathrm {tg} } ,{frac {pi }{n}}}

S=nr^{2}{mathop {{mathrm {tg}}}},{frac {pi }{n}}

(площадь основания n-угольной правильной призмы)

Площадь правильного многоугольника с числом сторон n{displaystyle n}

$n$ равна

S=nra2{displaystyle S={frac {nra}{2}}}

S={frac {nra}{2}}

где r{displaystyle r}

$r$ — расстояние от середины стороны до центра, a{displaystyle a} $a$ — длина стороны.

Площадь правильного многоугольника через периметр (P{displaystyle P}

$P$ ) и радиус вписанной окружности (r{displaystyle r} $r$ ) составляет:

S=12Pr{displaystyle S={frac {1}{2}}Pr}

S={frac {1}{2}}Pr

Периметр

Если нужно вычислить длину стороны(an) правильного n-угольника, вписанного в окружность, зная длину окружности(L) можно вычислить длину одной стороны многоугольника:

an{displaystyle a_{n}}

a_n

— длина стороны правильного n-угольника.

an=sin⁡180n⋅Lπ{displaystyle a_{n}=sin {frac {180}{n}}cdot {frac {L}{pi }}}

a_{n}=sin {frac {180}{n}}cdot {frac {L}{pi }}

Периметр Pn{displaystyle P_{n}}

$P_{n}$ равен

Pn=an⋅n{displaystyle P_{n}=a_{n}cdot n}

P_{n}=a_{n}cdot n

где n{displaystyle n}

$n$ — чилсо сторон многоугольника.

Применение

Правильными многоугольниками по определению являются грани правильных многогранников.

Древнегреческие математики (Антифонт, Брисон Гераклейский, Архимед и др.) использовали правильные многоугольники для вычисления числа π. Они вычисляли площади вписанных в окружность и описанных вокруг неё многоугольников, постепенно увеличивая число их сторон и получая таким образом оценку площади круга.[1]

История

Построение правильного многоугольника с n сторонами оставалось проблемой для математиков вплоть до XIX века. Такое построение идентично разделению окружности на n равных частей, так как соединив между собой точки, делящие окружность на части, можно получить искомый многоугольник.

Евклид в своих «Началах» занимался построением правильных многоугольников в книге IV, решая задачу для n = 3, 4, 5, 6, 15. Кроме этого, он уже определил первый критерий построимости многоугольников: хотя этот критерий и не был озвучен в «Началах», древнегреческие математики умели построить многоугольник с 2m сторонами (при целом m > 1), имея уже построенный многоугольник с числом сторон 2m — 1: пользуясь умением разбиения дуги на две части, из двух полуокружностей мы строим квадрат, потом правильный восьмиугольник, правильный шестнадцатиугольник и так далее. Кроме этого, в той же книге Эвклид указывает и второй критерий: если известно, как строить многоугольники с r и s сторонами, и r и s взаимно простые, то можно построить и многоугольник с r · s сторонами. Синтезируя эти два способа, можно прийти к выводу, что древние математики умели строить правильные многоугольники с 2m⋅p1k1⋅p2k2{displaystyle 2^{m}cdot {p_{1}}^{k_{1}}cdot {p_{2}}^{k_{2}}}

$2^{m}cdot {p_{1}}^{{k_{1}}}cdot {p_{2}}^{{k_{2}}}$ сторонами, где m — целое неотрицательное число, p1,p2{displaystyle {p_{1}},{p_{2}}} ${p_{1}},{p_{2}}$ — числа 3 и 5, а k1,k2{displaystyle {k_{1}},{k_{2}}} ${k_{1}},{k_{2}}$ принимают значения 0 или 1.

Средневековая математика почти никак не продвинулась в этом вопросе. Лишь в 1796 году Карлу Фридриху Гауссу удалось доказать, что если число сторон правильного многоугольника равно простому числу Ферма, то его можно построить при помощи циркуля и линейки. На сегодняшний день известны следующие простые числа Ферма: 3, 5, 17, 257, 65537. Вопрос о наличии или отсутствии других таких чисел остаётся открытым. Если брать в общем, из этого следует, что правильный многоугольник возможно построить, если число его сторон равно 2k0p1k1p2k2⋯psks{displaystyle 2^{k_{0}}{p_{1}}^{k_{1}}{p_{2}}^{k_{2}}cdots {p_{s}}^{k_{s}}}

$2^{{k_{0}}}{p_{1}}^{{k_{1}}}{p_{2}}^{{k_{2}}}cdots {p_{s}}^{{k_{s}}}$ , где k0{displaystyle {k_{0}}} ${k_{0}}$ — целое неотрицательное число, k1,k2,…,ks{displaystyle {k_{1}},{k_{2}},dots ,{k_{s}}} ${k_{1}},{k_{2}},dots ,{k_{s}}$ принимают значения 0 или 1, а pj{displaystyle {p_{j}}} ${p_{j}}$ — простые числа Ферма.

Гаусс подозревал, что это условие является не только достаточным, но и необходимым, но впервые это было доказано Пьером-Лораном Ванцелем в 1836 году.

Точку в деле построения правильных многоугольников поставило нахождение построений 17-, 257- и 65537-угольника. Первое было найдено Йоханнесом Эрхингером в 1825 году, второе — Фридрихом Юлиусом Ришело в 1832 году, а последнее — Иоганном Густавом Гермесом в 1894 году.

С тех пор проблема считается полностью решённой.

См. также

Правильный многогранник

Примечания

В Викисловаре есть статья «правильный многоугольник»

↑ А. В. Жуков. О числе π. — М.: МЦНМО, 2002. ISBN 5-94057-030-5.