Криволинейная система координат

Разделы:

Криволине́йная систе́ма координа́т, или криволине́йные координа́ты в математике — система координат в евклидовом (аффинном) пространстве, или в области, содержащейся в нём. Криволинейные координаты противопоставляются прямолинейным: декартовым, а также косоугольным. Применяются обычно на плоскости (n=2) и в пространстве (n=3); число координат равно размерности пространства n.Наиболее известным примером криволинейной системы координат являются полярные координаты на плоскости.

Содержание

1 Локальные свойства криволинейных координат
- 1.1 Общий случай
  - 1.1.1 Локальный базис и тензорный анализ
- 1.2 Ортогональные криволинейные координаты
  - 1.2.1 Коэффициенты Ламе
2 Примеры
3 Криволинейные координаты с точки зрения дифференциальной геометрии
4 Литература

Локальные свойства криволинейных координат

При рассмотрении криволинейных координат в данном разделе мы будем полагать, что рассматриваем трёхмерное пространство (n=3) снабжено декартовыми координатами x, y, z. Случай других размерностей отличается лишь количеством координат.

В случае евклидова пространства метрический тензор, именуемый также квадратом дифференциала дуги, будет в этих координатах иметь вид, соответствующий единичной матрице:

dS2=dx2+dy2+dz2.{displaystyle dS^{2}=mathbf {dx} ^{2}+mathbf {dy} ^{2}+mathbf {dz} ^{2}.}

dS^{2}={mathbf {dx}}^{2}+{mathbf {dy}}^{2}+{mathbf {dz}}^{2}.

Общий случай

Криволинейные координаты в трёхмерном аффинном пространстве

Пусть q1{displaystyle q_{1}}

$q_{1}$ , q2{displaystyle q_{2}} $q_{2}$ , q3{displaystyle q_{3}} $q_{3}$ — некие криволинейные координаты, которые мы будем считать заданные гладкими функциями от x, y, z.Для того, чтобы три функции q1{displaystyle q_{1}} $q_{1}$ , q2{displaystyle q_{2}} $q_{2}$ , q3{displaystyle q_{3}} $q_{3}$ служили координатами в некоторой области пространства, необходимо существование обратного отображения:

{x=φ1(q1,q2,q3);y=φ2(q1,q2,q3);z=φ3(q1,q2,q3),{displaystyle left{{begin{matrix}x=varphi _{1}left(q_{1},;q_{2},;q_{3}right);\y=varphi _{2}left(q_{1},;q_{2},;q_{3}right);\z=varphi _{3}left(q_{1},;q_{2},;q_{3}right),end{matrix}}right.}

left{{begin{matrix}x=varphi _{1}left(q_{1},;q_{2},;q_{3}right);\y=varphi _{2}left(q_{1},;q_{2},;q_{3}right);\z=varphi _{3}left(q_{1},;q_{2},;q_{3}right),end{matrix}}right.

где φ1,φ2,φ3{displaystyle varphi _{1},;varphi _{2},;varphi _{3}}

$varphi _{1},;varphi _{2},;varphi _{3}$ — функции, определённые в некоторой области наборов (q1,q2,q3){displaystyle left(q_{1},;q_{2},;q_{3}right)} $left(q_{1},;q_{2},;q_{3}right)$ координат.

Локальный базис и тензорный анализ

Этот раздел статьи ещё не написан. Здесь может располагаться отдельный раздел. Помогите Википедии, написав его.

Ортогональные криволинейные координаты

В евклидовом пространстве особое значение имеет использование ортогональных криволинейных координат, поскольку формулы, имеющие отношение к длине и углам, выглядят в ортогональных координатах проще, нежели в общем случае.

Коэффициенты Ламе

Выпишем дифференциал дуги в криволинейных координатах в виде (используется правило суммирования Эйнштейна):

dS2=(∂φ1∂qidqi)2+(∂φ2∂qidqi)2+(∂φ3∂qidqi)2, i=1,2,3{displaystyle dS^{2}=left({frac {partial varphi _{1}}{partial q_{i}}}mathbf {dq} _{i}right)^{2}+left({frac {partial varphi _{2}}{partial q_{i}}}mathbf {dq} _{i}right)^{2}+left({frac {partial varphi _{3}}{partial q_{i}}}mathbf {dq} _{i}right)^{2},~i=1,2,3}

dS^{2}=left({frac {partial varphi _{1}}{partial q_{i}}}{mathbf {dq}}_{i}right)^{2}+left({frac {partial varphi _{2}}{partial q_{i}}}{mathbf {dq}}_{i}right)^{2}+left({frac {partial varphi _{3}}{partial q_{i}}}{mathbf {dq}}_{i}right)^{2},~i=1,2,3

Принимая во внимание ортогональность систем координат (dqi⋅dqj=0{displaystyle mathbf {dq} _{i}cdot mathbf {dq} _{j}=0}

${mathbf {dq}}_{i}cdot {mathbf {dq}}_{j}=0$ при i≠j{displaystyle ineq j} $i ne j$ ) это выражение можно переписать в виде

dS2=H12dq12+H22dq22+H32dq32,{displaystyle dS^{2}=H_{1}^{2}dq_{1}^{2}+H_{2}^{2}dq_{2}^{2}+H_{3}^{2}dq_{3}^{2},}

dS^{2}=H_{1}^{2}dq_{1}^{2}+H_{2}^{2}dq_{2}^{2}+H_{3}^{2}dq_{3}^{2},

где

Hi=(∂φ1∂qi)2+(∂φ2∂qi)2+(∂φ3∂qi)2; i=1,2,3{displaystyle H_{i}={sqrt {left({frac {partial varphi _{1}}{partial q_{i}}}right)^{2}+left({frac {partial varphi _{2}}{partial q_{i}}}right)^{2}+left({frac {partial varphi _{3}}{partial q_{i}}}right)^{2}}}; i=1,;2,;3}

H_{i}={sqrt {left({frac {partial varphi _{1}}{partial q_{i}}}right)^{2}+left({frac {partial varphi _{2}}{partial q_{i}}}right)^{2}+left({frac {partial varphi _{3}}{partial q_{i}}}right)^{2}}}; i=1,;2,;3

Положительные величины Hi {displaystyle H_{i} }

$H_i$ , зависящие от точки пространства, именуются коэффициентами Ламе.

Тензор римановой метрики, записанный в координатах qi{displaystyle {q_{i}}}

${q_{i}}$ , представляет из себя диагональную матрицу, на диагонали которой стоя́т квадраты коэффициентов Ламе:

gii=Hi2{displaystyle g_{ii}={H_{i}}^{2}}

g_{{ii}}={H_{i}}^{2}

gij=0{displaystyle g_{ij}=0}

g_{{ij}}=0

для i≠j

, то есть

gij=(H12000H22000H32){displaystyle g_{ij}={begin{pmatrix}{H_{1}}^{2}&0&0\0&{H_{2}}^{2}&0\0&0&{H_{3}}^{2}end{pmatrix}}}

g_{{ij}}={begin{pmatrix}{H_{1}}^{2}&0&0\0&{H_{2}}^{2}&0\0&0&{H_{3}}^{2}end{pmatrix}}

Примеры

Полярные координаты (n=2)

Основная статья: Полярные координаты

Полярные координаты на плоскости включают расстояние r до полюса (начала координат) и направление (угол) φ.

Связь полярных координат с декартовыми:

{x=rcos⁡φ;y=rsin⁡φ.{displaystyle left{{begin{matrix}x=rcos {varphi };\y=rsin {varphi
}.end{matrix}}right.}

left{{begin{matrix}x=rcos {varphi };\y=rsin {varphi }.end{matrix}}right.

Коэффициенты Ламе:

Hr=1;Hφ=r.{displaystyle {begin{matrix}H_{r}=1;\H_{varphi }=r.end{matrix}}}

{begin{matrix}H_{r}=1;\H_{varphi }=r.end{matrix}}

Дифференциал дуги:

dS2 = dr2 + r2dφ2.{displaystyle dS^{2} = dr^{2} + r^{2}dvarphi ^{2}.}

dS^{2} = dr^{2} + r^{2}dvarphi ^{2}.

В начале координат функция φ не определена.Если координату φ считать не числом, а углом (точкой на единичной окружности), то полярные координаты образуют систему координат в области, полученной изо всей плоскости изъятием точки начала координат. Если всё-таки считать φ числом, то в означенной области оно будет многозначно, и построение строго в математическом смысле системы координат возможно лишь в односвязной области, не включающей начало координат, например, на плоскости без луча.

Цилиндрические координаты (n=3)

Основная статья: Цилиндрические координаты

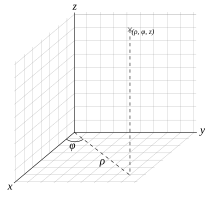
Цилиндрические координаты являются тривиальным обобщением полярных на случай трёхмерного пространства путём добавления третьей координаты z.Связь цилиндрических координат с декартовыми:

{x=rcos⁡φ;y=rsin⁡φ.z=z.{displaystyle left{{begin{matrix}x=rcos {varphi };\y=rsin {varphi }.\z=z.end{matrix}}right.}

left{{begin{matrix}x=rcos {varphi };\y=rsin {varphi }.\z=z.end{matrix}}right.

Коэффициенты Ламе:

Hr=1;Hφ=r;Hz=1.{displaystyle {begin{matrix}H_{r}=1;\H_{varphi }=r;\H_{z}=1.end{matrix}}}

{begin{matrix}H_{r}=1;\H_{varphi }=r;\H_{z}=1.end{matrix}}

Дифференциал дуги:

dS2 = dr2 + r2dφ2+dz2.{displaystyle dS^{2} = dr^{2} + r^{2}dvarphi ^{2}+dz^{2}.}

dS^{2} = dr^{2} + r^{2}dvarphi ^{2}+dz^{2}.

Сферические координаты (n=3)

Основная статья: Сферические координаты

Сферические координаты связаны с координатами широты и долготы на единичной сфере.Связь сферических координат с декартовыми:

{x=rsin⁡θcos⁡φ;y=rsin⁡θsin⁡φ;z=rcos⁡θ.{displaystyle left{{begin{matrix}x=rsin {theta }cos {varphi };\y=rsin {theta }sin {varphi };\z=rcos {theta }.end{matrix}}right.}

left{{begin{matrix}x=rsin {theta }cos {varphi };\y=rsin {theta }sin {varphi };\z=rcos {theta }.end{matrix}}right.

Коэффициенты Ламе:

Hr=1;Hθ=r;Hφ=rsin⁡θ.{displaystyle {begin{matrix}H_{r}=1;\H_{theta }=r;\H_{varphi }=rsin {theta }.end{matrix}}}

{begin{matrix}H_{r}=1;\H_{theta }=r;\H_{varphi }=rsin {theta }.end{matrix}}

Дифференциал дуги:

dS2 = dr2 + r2dθ2+r2sin2⁡θdφ2.{displaystyle dS^{2} = dr^{2} + r^{2}dtheta ^{2}+r^{2}sin ^{2}{theta }dvarphi ^{2}.}

dS^{2} = dr^{2} + r^{2}dtheta ^{2}+r^{2}sin ^{2}{theta }dvarphi ^{2}.

Сферические координаты, как и цилиндрические, не работают на оси z {x=0, y=0}, поскольку координата φ там не определена.

Различные экзотические координаты на плоскости (n=2) и их обобщения

Ортогональные:

Эллиптические координаты — расширяются до 3 измерений
Параболические координаты — расширяются до 3 измерений
Биполярные координаты — расширяются до 3 измерений
…

Прочие:

…

Криволинейные координаты с точки зрения дифференциальной геометрии

Криволинейные координаты, определённые в различных областях евклидова (аффинного) пространства, можно рассматривать как применение к пространству понятия гладкого многообразия. А именно, как построение атласа карт.

Литература

Корн Г., Корн Т. Справочник по математике (для научных работников и инженеров). — М.: Наука, 1974. — 832 с.

В другом языковом разделе есть более полная статья Curvilinear coordinates (англ.). Вы можете помочь проекту, расширив текущую статью с помощью перевода