Параболические координаты — ортогональная система координат на плоскости, в которой координатные линии являются конфокальными параболами. Трёхмерный вариант этой системы координат получается при вращении парабол вокруг их оси симметрии.
Параболические координаты нашли многочисленные применения в математической физике, в частности, в теории эффекта Штарка и задаче о потенциале вблизи угла.
Содержание
- 1 Двумерные параболические координаты
- 2 Дифференциальные характеристики двумерных координат
- 3 Трёхмерные параболические координаты
- 4 Дифференциальные характеристики трёхмерных координат
- 5 Обратные преобразования
- 6 Внешние ссылки
Двумерные параболические координаты
Двумерные параболические координаты (σ,τ){displaystyle (sigma ,;tau )}
определяются выражениями
- x=στ,{displaystyle x=sigma tau ,}
- y=12(τ2−σ2).{displaystyle y={frac {1}{2}}(tau ^{2}-sigma ^{2}).}
Поверхности постоянной σ{displaystyle sigma }
являются конфокальными параболами
- 2y=x2σ2−σ2{displaystyle 2y={frac {x^{2}}{sigma ^{2}}}-sigma ^{2}}
расширяющимися вверх (вдоль луча +y{displaystyle +y}
), а поверхности постоянной τ{displaystyle tau } — это конфокальные параболы
- 2y=−x2τ2+τ2{displaystyle 2y=-{frac {x^{2}}{tau ^{2}}}+tau ^{2}}
расширяющиеся вниз (вдоль луча −y{displaystyle -y}
). Фокусы всех парабол расположены в начале коорднат.
Дифференциальные характеристики двумерных координат
Коэффициенты Ламэ для параболических кординат равны
- Hσ=Hτ=σ2+τ2.{displaystyle H_{sigma }=H_{tau }={sqrt {sigma ^{2}+tau ^{2}}}.}
Таким образом, элемент площади равен
- dS=(σ2+τ2)dσdτ,{displaystyle dS=(sigma ^{2}+tau ^{2}),dsigma ,dtau ,}
а лапласиан равен
- ΔΦ=1σ2+τ2(∂2Φ∂σ2+∂2Φ∂τ2).{displaystyle Delta Phi ={frac {1}{sigma ^{2}+tau ^{2}}}left({frac {partial ^{2}Phi }{partial sigma ^{2}}}+{frac {partial ^{2}Phi }{partial tau ^{2}}}right).}
Прочие дифференциальные операторы могут быть аналогично найдены подстановкой коэффициентов Ламэ в соответствующую общую формулу.
Трёхмерные параболические координаты
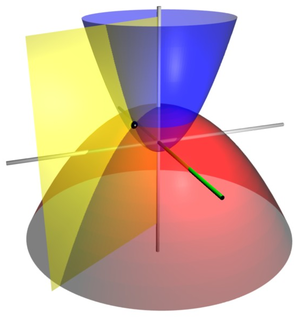 Координатные поверхности для трёхмерных параболических координат. Красный параболоид соответствует τ=2{displaystyle scriptstyle {tau =2}} , синий параболоид соответствует σ=1{displaystyle scriptstyle {sigma =1}} , а жёлтая полуплоскость соответствует φ=−60∘{displaystyle scriptstyle {varphi =-60^{circ }}} . Три поверхности пересекаются в точке P{displaystyle scriptstyle {P}} (отмеченной чёрной сферой), имеющей декартовы координаты приблизительно (1,0,−1,732,1,5){displaystyle scriptstyle {(1{,}0,;-1{,}732,;1{,}5)}} .
Координатные поверхности для трёхмерных параболических координат. Красный параболоид соответствует τ=2{displaystyle scriptstyle {tau =2}} , синий параболоид соответствует σ=1{displaystyle scriptstyle {sigma =1}} , а жёлтая полуплоскость соответствует φ=−60∘{displaystyle scriptstyle {varphi =-60^{circ }}} . Три поверхности пересекаются в точке P{displaystyle scriptstyle {P}} (отмеченной чёрной сферой), имеющей декартовы координаты приблизительно (1,0,−1,732,1,5){displaystyle scriptstyle {(1{,}0,;-1{,}732,;1{,}5)}} .
На основе двумерных параболических координат строятся два типа трёхмерных координат. Первые получаются простым проектированием на плоскость XY{displaystyle XY}
вдоль оси z{displaystyle z} и называются цилиндрические параболические координаты.
Вторая система координат, также называемая «параболические координаты», строится на основе параболоидов вращения, получаемых вращением парабол вокруг их оси симметрии
- {x=στcosφ,y=στsinφ,z=12(τ2−σ2).{displaystyle {begin{cases}x=sigma tau cos varphi ,\y=sigma tau sin varphi ,\z={dfrac {1}{2}}(tau ^{2}-sigma ^{2}).end{cases}}}
Ось параболоидов совпадает с осью z{displaystyle z}
, так как вокруг неё производится вращение. Азимутальный угол φ{displaystyle varphi } определяется как
- tgφ=yx.{displaystyle mathrm {tg} ,varphi ={frac {y}{x}}.}
Поверхности постоянной σ{displaystyle sigma }
являются конфокальными параболоидами
- 2z=x2+y2σ2−σ2{displaystyle 2z={frac {x^{2}+y^{2}}{sigma ^{2}}}-sigma ^{2}}
направленными вверх (вдоль луча +z{displaystyle +z}
), а поверхности постоянной τ{displaystyle tau } — это конфокальные параболоиды
- 2z=−x2+y2τ2+τ2{displaystyle 2z=-{frac {x^{2}+y^{2}}{tau ^{2}}}+tau ^{2}}
направленные вниз (вдоль луча −z{displaystyle -z}
). Фокусы всех параболоидов расположены в начале координат.
Дифференциальные характеристики трёхмерных координат
Коэффициенты Ламэ в трёхмерном случае:
- Hσ=σ2+τ2,{displaystyle H_{sigma }={sqrt {sigma ^{2}+tau ^{2}}},}
- Hτ=σ2+τ2,{displaystyle H_{tau }={sqrt {sigma ^{2}+tau ^{2}}},}
- Hφ=στ.{displaystyle H_{varphi }=sigma tau .}
Как видно, коэффициенты Hσ{displaystyle H_{sigma }}
и Hτ{displaystyle H_{tau }} совпадают с двумерным случаем. Элемент объёма равен
- dV=hσhτhφ=στ(σ2+τ2)dσdτdφ,{displaystyle dV=h_{sigma }h_{tau }h_{varphi }=sigma tau (sigma ^{2}+tau ^{2}),dsigma ,dtau ,dvarphi ,}
а лапласиан равен
- ∇2Φ=1σ2+τ2[1σ∂∂σ(σ∂Φ∂σ)+1τ∂∂τ(τ∂Φ∂τ)]+1σ2τ2∂2Φ∂φ2.{displaystyle nabla ^{2}Phi ={frac {1}{sigma ^{2}+tau ^{2}}}left[{frac {1}{sigma }}{frac {partial }{partial sigma }}left(sigma {frac {partial Phi }{partial sigma }}right)+{frac {1}{tau }}{frac {partial }{partial tau }}left(tau {frac {partial Phi }{partial tau }}right)right]+{frac {1}{sigma ^{2}tau ^{2}}}{frac {partial ^{2}Phi }{partial varphi ^{2}}}.}
Прочие дифференциальные операторы, такие как дивергенция или ротор могут быть аналогично найдены подстановкой коэффициентов Ламэ в соответствующую общую формулу.
Обратные преобразования
Переход от декартовых координат (x,y,z){displaystyle (x,;y,;z)}
к параболическим (η,ξ,φ){displaystyle (eta ,;xi ,;varphi )} осуществляется по формулам:
- {η=−z+x2+y2+z2,ξ=z+x2+y2+z2,φ=arctgyx,{displaystyle {begin{cases}eta =-z+{sqrt {x^{2}+y^{2}+z^{2}}},\xi =z+{sqrt {x^{2}+y^{2}+z^{2}}},\varphi =mathrm {arctg} {dfrac {y}{x}},end{cases}}}
при этом η⩾0,ξ⩾0.{displaystyle eta geqslant 0,quad xi geqslant 0.}
- |dηdξdφ|=|xx2+y2+z2yx2+y2+z2−1+zx2+y2+z2xx2+y2+z2yx2+y2+z21+zx2+y2+z2−yx2+y2xx2+y20|⋅|dxdydz|.{displaystyle {begin{vmatrix}deta \dxi \dvarphi end{vmatrix}}={begin{vmatrix}{dfrac {x}{sqrt {x^{2}+y^{2}+z^{2}}}}&{dfrac {y}{sqrt {x^{2}+y^{2}+z^{2}}}}&-1+{dfrac {z}{sqrt {x^{2}+y^{2}+z^{2}}}}\{dfrac {x}{sqrt {x^{2}+y^{2}+z^{2}}}}&{dfrac {y}{sqrt {x^{2}+y^{2}+z^{2}}}}&1+{dfrac {z}{sqrt {x^{2}+y^{2}+z^{2}}}}\{dfrac {-y}{x^{2}+y^{2}}}&{dfrac {x}{x^{2}+y^{2}}}&0end{vmatrix}}cdot {begin{vmatrix}dx\dy\dzend{vmatrix}}.}
При φ=0{displaystyle varphi =0}
получаем ограничение координат на плоскость XZ{displaystyle XZ} :
- η=−z+x2+z2,{displaystyle eta =-z+{sqrt {x^{2}+z^{2}}},}
- ξ=z+x2+z2.{displaystyle xi =z+{sqrt {x^{2}+z^{2}}}.}
Линия уровня η=c{displaystyle eta =c}
:
- z|η=c=x22c−c2.{displaystyle z|_{eta =c}={frac {x^{2}}{2c}}-{frac {c}{2}}.}
Это парабола, фокус которой при любом c{displaystyle c}
расположен в начале координат.
Аналогично при ξ=c{displaystyle xi =c}
получаем
- z|ξ=c=c2−x22c.{displaystyle z|_{xi =c}={frac {c}{2}}-{frac {x^{2}}{2c}}.}
Координатные параболы пересекаются в точке
- P:(bc,b−c2).{displaystyle P:left({sqrt {bc}},;{frac {b-c}{2}}right).}
- dzcdx=xc=bcc=bc=sc,{displaystyle {frac {dz_{c}}{dx}}={frac {x}{c}}={frac {sqrt {bc}}{c}}={sqrt {frac {b}{c}}}=s_{c},}
- dzbdx=−xb=−bcb=−cb=sb;{displaystyle {frac {dz_{b}}{dx}}=-{frac {x}{b}}={frac {-{sqrt {bc}}}{b}}=-{sqrt {frac {c}{b}}}=s_{b};}
- scsb=−bccb=−1.{displaystyle s_{c}s_{b}=-{sqrt {frac {b}{c}}}{sqrt {frac {c}{b}}}=-1.}
- {x=ξηcosφ,y=ξηsinφ,z=12(ξ−η).{displaystyle {begin{cases}x={sqrt {xi eta }}cos varphi ,\y={sqrt {xi eta }}sin varphi ,\z={dfrac {1}{2}}(xi -eta ).end{cases}}}
- |dxdydz|=|12ξηcosφ12ηξcosφ−ξηsinφ12ξηsinφ12ηξsinφξηcosφ−12120|⋅|dηdξdφ|.{displaystyle {begin{vmatrix}dx\dy\dzend{vmatrix}}={begin{vmatrix}{dfrac {1}{2}}{sqrt {dfrac {xi }{eta }}}cos varphi &{dfrac {1}{2}}{sqrt {dfrac {eta }{xi }}}cos varphi &-{sqrt {xi eta }}sin varphi \{dfrac {1}{2}}{sqrt {dfrac {xi }{eta }}}sin varphi &{dfrac {1}{2}}{sqrt {dfrac {eta }{xi }}}sin varphi &{sqrt {xi eta }}cos varphi \-{dfrac {1}{2}}&{dfrac {1}{2}}&0end{vmatrix}}cdot {begin{vmatrix}deta \dxi \dvarphi end{vmatrix}}.}
Пара парабол пересекается в двух точках, но при φ=0{displaystyle varphi =0}
точка оказывается заключена в полуплоскости x>0{displaystyle x>0} , так как x<0{displaystyle x<0} соответствует φ=π{displaystyle varphi =pi } .
Найдём коэффициенты наклоны касательных к параболам в точке P{displaystyle P}
:
Так как произведение коэффициентов равно −1, то параболы перпендикулярны в точке пересечения. Таким образом, параболические координаты оказываются ортогональными.
Пара (ξ;η){displaystyle (xi ;;eta )}
определяет координаты в полуплоскости. При изменении φ{displaystyle varphi } от 0 до 2π{displaystyle 2pi } полуплоскость вращается вокруг оси z{displaystyle z} , в качестве координатных поверхностей получются параболоиды вращения и полуплоскости. Пара противоположных параболоидов определяет круг, а величина φ{displaystyle varphi } определяет полуплоскость, пересекающую круг в единственной точке. Её декартовы координаты равны:
Внешние ссылки
Weisstein, Eric W. Parabolic Coordinates (англ.) на сайте Wolfram MathWorld.


 определяются выражениями
определяются выражениями

 являются конфокальными параболами
являются конфокальными параболами
 ), а поверхности постоянной τ{displaystyle tau }
), а поверхности постоянной τ{displaystyle tau } — это конфокальные параболы
— это конфокальные параболы
 ). Фокусы всех парабол расположены в начале коорднат.
). Фокусы всех парабол расположены в начале коорднат.


 , синий параболоид соответствует σ=1{displaystyle scriptstyle {sigma =1}}
, синий параболоид соответствует σ=1{displaystyle scriptstyle {sigma =1}} , а жёлтая полуплоскость соответствует φ=−60∘{displaystyle scriptstyle {varphi =-60^{circ }}}
, а жёлтая полуплоскость соответствует φ=−60∘{displaystyle scriptstyle {varphi =-60^{circ }}} . Три поверхности пересекаются в точке P{displaystyle scriptstyle {P}}
. Три поверхности пересекаются в точке P{displaystyle scriptstyle {P}} (отмеченной чёрной сферой), имеющей декартовы координаты приблизительно (1,0,−1,732,1,5){displaystyle scriptstyle {(1{,}0,;-1{,}732,;1{,}5)}}
(отмеченной чёрной сферой), имеющей декартовы координаты приблизительно (1,0,−1,732,1,5){displaystyle scriptstyle {(1{,}0,;-1{,}732,;1{,}5)}} .
. вдоль оси z{displaystyle z} и называются
вдоль оси z{displaystyle z} и называются 
 , так как вокруг неё производится вращение. Азимутальный угол φ{displaystyle varphi }
, так как вокруг неё производится вращение. Азимутальный угол φ{displaystyle varphi } определяется как
определяется как
 являются конфокальными параболоидами
являются конфокальными параболоидами
 ), а поверхности постоянной τ{displaystyle tau }
), а поверхности постоянной τ{displaystyle tau }
 ). Фокусы всех параболоидов расположены в начале координат.
). Фокусы всех параболоидов расположены в начале координат.


 и Hτ{displaystyle H_{tau }}
и Hτ{displaystyle H_{tau }} совпадают с двумерным случаем. Элемент объёма равен
совпадают с двумерным случаем. Элемент объёма равен
![{displaystyle nabla ^{2}Phi ={frac {1}{sigma ^{2}+tau ^{2}}}left[{frac {1}{sigma }}{frac {partial }{partial sigma }}left(sigma {frac {partial Phi }{partial sigma }}right)+{frac {1}{tau }}{frac {partial }{partial tau }}left(tau {frac {partial Phi }{partial tau }}right)right]+{frac {1}{sigma ^{2}tau ^{2}}}{frac {partial ^{2}Phi }{partial varphi ^{2}}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c364ac2414a85d4b98704013938e5776593acb8b)
 к параболическим (η,ξ,φ){displaystyle (eta ,;xi ,;varphi )}
к параболическим (η,ξ,φ){displaystyle (eta ,;xi ,;varphi )} осуществляется по формулам:
осуществляется по формулам:


 получаем ограничение координат на плоскость XZ{displaystyle XZ}
получаем ограничение координат на плоскость XZ{displaystyle XZ} :
:

 :
:
 расположен в начале координат.
расположен в начале координат. получаем
получаем

 , так как x<0{displaystyle x<0}
, так как x<0{displaystyle x<0} соответствует φ=π{displaystyle varphi =pi }
соответствует φ=π{displaystyle varphi =pi } .
. :
:


 определяет координаты в полуплоскости. При изменении φ{displaystyle varphi }
определяет координаты в полуплоскости. При изменении φ{displaystyle varphi } полуплоскость вращается вокруг оси z{displaystyle z}
полуплоскость вращается вокруг оси z{displaystyle z}

