wiki

Обратные тригонометрические функции

Обра́тные тригонометри́ческие фу́нкции (круговые функции, аркфункции) — математические функции, являющиеся обратными к тригонометрическим функциям. К обратным тригонометрическим функциям обычно относят шесть функций:

  • арксинус (обозначение: arcsin⁡x;{displaystyle arcsin x;} угол, синус которого равен x{displaystyle x})
  • арккосинус (обозначение: arccos⁡x;{displaystyle arccos x;} угол, косинус которого равен x{displaystyle x} и т. д.)
  • арктангенс (обозначение: arctg⁡x{displaystyle operatorname {arctg} x}; в иностранной литературе arctan⁡x{displaystyle arctan x})
  • арккотангенс (обозначение: arcctg⁡x{displaystyle operatorname {arcctg} x}; в иностранной литературе arccot⁡x{displaystyle operatorname {arccot} x} или arccotan⁡x{displaystyle operatorname {arccotan} x})
  • арксеканс (обозначение: arcsec⁡x{displaystyle operatorname {arcsec} x})
  • арккосеканс (обозначение: arccosec⁡x{displaystyle operatorname {arccosec} x}; в иностранной литературе arccsc⁡x{displaystyle operatorname {arccsc} x})

Название обратной тригонометрической функции образуется от названия соответствующей ей тригонометрической функции добавлением приставки «арк-» (от лат. arcus — дуга). Это связано с тем, что геометрически значение обратной тригонометрической функции можно связать с длиной дуги единичной окружности (или углом, стягивающим эту дугу), соответствующей тому или иному отрезку. Так, обычный синус позволяет по дуге окружности найти стягивающую её хорду, а обратная функция решает противоположную задачу. Манера обозначать таким образом обратные тригонометрических функции появилась у австрийского математика Карла Шерфера (нем. Karl Scherffer; 1716—1783) и закрепилась благодаря Лагранжу. Впервые специальный символ для обратной тригонометрической функции использовал Даниил Бернулли в 1729 году. Английская и немецкая математические школы до конца XIX века предлагали иные обозначения: sin−1,1sin,{displaystyle sin ^{-1},{frac {1}{sin }},} но они не прижились[1].Лишь изредка в иностранной литературе, также как и в научных/инженерных калькуляторах, пользуются обозначениями типа sin−1, cos−1 для арксинуса, арккосинуса и т. п.[2], — такая запись считается не очень удобной, так как возможна путаница с возведением функции в степень −1.

Тригонометрические функции периодичны, поэтому функции, обратные к ним, многозначны. То есть, значение аркфункции представляет собой множество углов (дуг), для которых соответствующая прямая тригонометрическая функция равна заданному числу. Например, arcsin⁡1/2{displaystyle arcsin 1/2} означает множество углов (π6,5π6,13π6,17π6… (30∘,150∘,390∘,510∘…)){displaystyle left({frac {pi }{6}},{frac {5pi }{6}},{frac {13pi }{6}},{frac {17pi }{6}}dots ~(30^{circ },150^{circ },390^{circ },510^{circ }dots )right)}, синус которых равен 1/2{displaystyle 1/2}. Из множества значений каждой аркфункции выделяют её главные значения (см. графики главных значений аркфункций ниже), которые обычно и имеют в виду, говоря об арксинусе, арккосинусе и т. д.

В общем случае при условии −1⩽α⩽1{displaystyle -1leqslant alpha leqslant 1} все решения уравнения sin⁡x=α{displaystyle sin x=alpha } можно представить в виде x=(−1)narcsin⁡α+πn, n=0,±1,±2,… .{displaystyle x=(-1)^{n}arcsin alpha +pi n,~n=0,pm 1,pm 2,dots ~.}[3]

Содержание

Основное соотношение

arcsin⁡x+arccos⁡x=π2{displaystyle arcsin x+arccos x={frac {pi }{2}}} 
arctgx+arcctgx=π2{displaystyle operatorname {arctg} ,x+operatorname {arcctg} ,x={frac {pi }{2}}} 

Функция arcsin

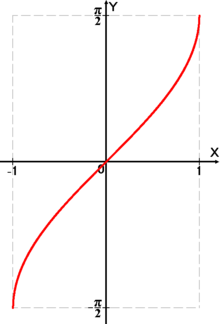  График функции y=arcsin⁡x{displaystyle y=arcsin x} 

Аркси́нусом числа x называется такое значение угла y, выраженного в радианах, для которого sin⁡y=x,−π2⩽y⩽π2,|x|⩽1.{displaystyle sin y=x,quad -{frac {pi }{2}}leqslant yleqslant {frac {pi }{2}},quad |x|leqslant 1.}

 

Функция y=arcsin⁡x{displaystyle y=arcsin x}

  непрерывна и ограничена на всей своей области определения. Она является строго возрастающей.

  • sin⁡(arcsin⁡x)=x{displaystyle sin(arcsin x)=xqquad }  при −1⩽x⩽1,{displaystyle -1leqslant xleqslant 1,} 
  • arcsin⁡(sin⁡y)=y{displaystyle arcsin(sin y)=yqquad }  при −π2⩽y⩽π2,{displaystyle -{frac {pi }{2}}leqslant yleqslant {frac {pi }{2}},} 
  • D(arcsin⁡x)=[−1;1]{displaystyle D(arcsin x)=[-1;1]qquad }  (область определения),
  • E(arcsin⁡x)=[−π2;π2]{displaystyle E(arcsin x)=left[-{frac {pi }{2}};{frac {pi }{2}}right]qquad }  (область значений).

Свойства функции arcsin

  • arcsin⁡(−x)=−arcsin⁡x{displaystyle arcsin(-x)=-arcsin xqquad }  (функция является нечётной).
  • arcsin⁡x>0{displaystyle arcsin x>0}  при 0<x⩽1{displaystyle 0<xleqslant 1} .
  • arcsin⁡x=0{displaystyle arcsin x=0}  при x=0.{displaystyle x=0.} 
  • arcsin⁡x<0{displaystyle arcsin x<0}  при −1⩽x<0.{displaystyle -1leqslant x<0.} 
  • arcsin⁡x={arccos⁡1−x2,0⩽x⩽1−arccos⁡1−x2,−1⩽x<0{displaystyle arcsin x=left{{begin{matrix}arccos {sqrt {1-x^{2}}},qquad 0leqslant xleqslant 1-arccos {sqrt {1-x^{2}}},qquad -1leqslant x<0end{matrix}}right.} 
  • arcsin⁡x=arctg⁡x1−x2{displaystyle arcsin x=operatorname {arctg} {frac {x}{sqrt {1-x^{2}}}}} 
  • arcsin⁡x={arcctg1−x2x,0<x⩽1arcctg1−x2x−π,−1⩽x<0{displaystyle arcsin x=left{{begin{matrix}operatorname {arcctg} ,{frac {sqrt {1-x^{2}}}{x}},qquad 0<xleqslant 1operatorname {arcctg} ,{frac {sqrt {1-x^{2}}}{x}}-pi ,qquad -1leqslant x<0end{matrix}}right.} 

Получение функции arcsin

Дана функция y=sin⁡x.{displaystyle y=sin x.}

  На всей своей области определения она является кусочно-монотонной, и, значит, обратное соответствие y=arcsin⁡x{displaystyle y=arcsin x}  функцией не является. Поэтому мы рассмотрим отрезок, на котором она строго возрастает и принимает все значения области значений — [−π2;π2]{displaystyle left[-{frac {pi }{2}};{frac {pi }{2}}right]} . Так как для функции y=sin⁡x{displaystyle y=sin x}  на интервале [−π2;π2]{displaystyle left[-{frac {pi }{2}};{frac {pi }{2}}right]}  каждое значение функции достигается при единственном значении аргумента, то на этом отрезке существует обратная функция y=arcsin⁡x,{displaystyle y=arcsin x,}  график которой симметричен графику функции y=sin⁡x{displaystyle y=sin x}  на отрезке [−π2;π2]{displaystyle left[-{frac {pi }{2}};{frac {pi }{2}}right]}  относительно прямой y=x.{displaystyle y=x.}  (графики взаимно обратных функций симметричны относительно биссектрисы первого и третьего координатных углов координатной плоскости Oxy{displaystyle Oxy} )

Функция arccos

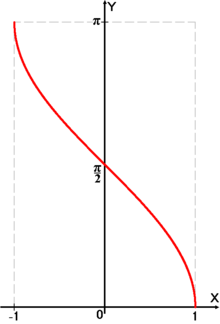  График функции y=arccos⁡x{displaystyle y=arccos x} 

Аркко́синусом числа x называется такое значение угла y в радианной мере, для которого cos⁡y=x,0⩽y⩽π,|x|⩽1.{displaystyle cos y=x,qquad 0leqslant yleqslant pi ,|x|leqslant 1.}

 

Функция y=arccos⁡x{displaystyle y=arccos x}

  непрерывна и ограничена на всей своей области определения. Она является строго убывающей и неотрицательной.

  • cos⁡(arccos⁡x)=x{displaystyle cos(arccos x)=x}  при −1⩽x⩽1,{displaystyle -1leqslant xleqslant 1,} 
  • arccos⁡(cos⁡y)=y{displaystyle arccos(cos y)=y}  при 0⩽y⩽π.{displaystyle 0leqslant yleqslant pi .} 
  • D(arccos⁡x)=[−1;1]{displaystyle D(arccos x)=[-1;1]}  (область определения),
  • E(arccos⁡x)=[0;π]{displaystyle E(arccos x)=[0;pi ]}  (область значений).

Свойства функции arccos

Получение функции arccos

Дана функция y=cos⁡x.{displaystyle y=cos x.}

  На всей своей области определения она является кусочно-монотонной, и, значит, обратное соответствие y=arccos⁡x{displaystyle y=arccos x}  функцией не является. Поэтому мы рассмотрим отрезок, на котором она строго убывает и принимает все свои значения — [0;π].{displaystyle [0;pi ].}  На этом отрезке y=cos⁡x{displaystyle y=cos x}  строго монотонно убывает и принимает все свои значения только один раз, а значит, на отрезке [0;π]{displaystyle [0;pi ]}  существует обратная функция y=arccos⁡x,{displaystyle y=arccos x,}  график которой симметричен графику y=cos⁡x{displaystyle y=cos x}  на отрезке [0;π]{displaystyle [0;pi ]}  относительно прямой y=x.{displaystyle y=x.} 

Функция arctg

  График функции y=arctgx{displaystyle y=operatorname {arctg} ,x} 

Аркта́нгенсом числа x называется такое значение угла y,{displaystyle y,}

  выраженное в радианах, для которого tg⁡y=x,−π2<y<π2.{displaystyle operatorname {tg} y=x,quad -{frac {pi }{2}}<y<{frac {pi }{2}}.} 

Функция y=arctg⁡x{displaystyle y=operatorname {arctg} x}

  определена на всей числовой прямой, всюду непрерывна и ограничена. Она является строго возрастающей.

  • tg(arctgx)=x{displaystyle operatorname {tg} ,(operatorname {arctg} ,x)=x}  при x∈R,{displaystyle xin mathbb {R} ,} 
  • arctg(tgy)=y{displaystyle operatorname {arctg} ,(operatorname {tg} ,y)=y}  при −π2<y<π2,{displaystyle -{frac {pi }{2}}<y<{frac {pi }{2}},} 
  • D(arctgx)=(−∞;∞){displaystyle D(operatorname {arctg} ,x)=(-infty ;infty )}  (область определения),
  • E(arctgx)=(−π2;π2){displaystyle E(operatorname {arctg} ,x)=left(-{frac {pi }{2}};{frac {pi }{2}}right)}  (область значений).

Свойства функции arctg

  • arctg⁡(−x)=−arctg⁡x{displaystyle operatorname {arctg} (-x)=-operatorname {arctg} xqquad }  (функция является нечётной).
  • arctg⁡x=arcsin⁡x1+x2.{displaystyle operatorname {arctg} x=arcsin {frac {x}{sqrt {1+x^{2}}}}.} 
  • arctg⁡x=arccos⁡11+x2{displaystyle operatorname {arctg} x=arccos {frac {1}{sqrt {1+x^{2}}}}} , при x > 0.
  • arctg⁡x=arcctg⁡1x.{displaystyle operatorname {arctg} x=operatorname {arcctg} {frac {1}{x}}.} 
  • arctg⁡x=−iarth⁡ix{displaystyle operatorname {arctg} x=-ioperatorname {arth} {ix}} , где arth{displaystyle operatorname {arth} }  — гиперболический арктангенс.
  • arth⁡x=iarctg⁡ix.{displaystyle operatorname {arth} x=ioperatorname {arctg} {ix}.} 

Получение функции arctg

Дана функция y=tgx.{displaystyle y=operatorname {tg} ,x.}

  На всей своей области определения она является кусочно-монотонной, и, значит, обратное соответствие y=arctgx{displaystyle y=operatorname {arctg} ,x}  функцией не является (так как нарушается требование однозначности). Поэтому рассмотрим отрезок, на котором она строго возрастает и принимает все свои значения только один раз — (−π2;π2).{displaystyle left(-{frac {pi }{2}};{frac {pi }{2}}right).}  На этом отрезке y=tgx{displaystyle y=operatorname {tg} ,x}  строго монотонно возрастает и принимает все свои значения только один раз, следовательно, на интервале (−π2;π2){displaystyle left(-{frac {pi }{2}};{frac {pi }{2}}right)}  существует обратная y=arctgx{displaystyle y=operatorname {arctg} ,x} , график которой симметричен графику y=tgx{displaystyle y=operatorname {tg} ,x}  на отрезке (−π2;π2){displaystyle left(-{frac {pi }{2}};{frac {pi }{2}}right)}  относительно прямой y=x.{displaystyle y=x.} 

Функция arcctg

  График функции y=arcctg⁡x{displaystyle y=operatorname {arcctg} x} 

Арккота́нгенсом числа x называется такое значение угла y (в радианной мере измерения углов), для которого ctgy=x,0<y<π.{displaystyle operatorname {ctg} ,y=x,quad 0<y<pi .}

 

Функция y=arcctgx{displaystyle y=operatorname {arcctg} ,x}

  определена на всей числовой прямой, всюду непрерывна и ограничена. Она является строго убывающей и всюду положительной.

  • ctg⁡(arcctgx)=x{displaystyle operatorname {ctg} (operatorname {arcctg} ,x)=x}  при x∈R,{displaystyle xin mathbb {R} ,} 
  • arcctg⁡(ctgy)=y{displaystyle operatorname {arcctg} (operatorname {ctg} ,y)=y}  при 0<y<π,{displaystyle 0<y<pi ,} 
  • D(arcctg⁡x)=(−∞;∞),{displaystyle D(operatorname {arcctg} x)=(-infty ;infty ),} 
  • E(arcctg⁡x)=(0;π).{displaystyle E(operatorname {arcctg} x)=(0;pi ).} 

Свойства функции arcctg

Получение функции arcctg

Дана функция y=ctgx{displaystyle y=operatorname {ctg} ,x}

 . На всей своей области определения она является кусочно-монотонной, и, значит, обратное соответствие y=arcctgx{displaystyle y=operatorname {arcctg} ,x}  функцией не является. Поэтому рассмотрим промежуток, на котором она строго убывает и принимает все свои значения только один раз — (0;π){displaystyle (0;pi )} . На этом отрезке y=ctgx{displaystyle y=operatorname {ctg} ,x}  строго убывает и принимает все свои значения только один раз, следовательно, на интервале (0;π){displaystyle (0;pi )}  существует обратная функция y=arcctgx{displaystyle y=operatorname {arcctg} ,x} , график которой симметричен графику y=ctgx{displaystyle y=operatorname {ctg} ,x}  на отрезке (0;π){displaystyle (0;pi )}  относительно прямой y=x.{displaystyle y=x.} 

График арккотангенса получается из графика арктангенса, если последний отразить относительно оси ординат (то есть заменить знак аргумента, x→−x{displaystyle xrightarrow -x}

 ) и сместить вверх на π/2; это вытекает из вышеупомянутой формулы arcctg⁡x=arctg⁡(−x)+π/2.{displaystyle operatorname {arcctg} x=operatorname {arctg} (-x)+pi /2.} 

Функция arcsec

  График функции y=arcsec⁡x{displaystyle y=operatorname {arcsec} x} 

Арксе́кансом числа x называется такое значение угла y (в радианной мере измерения углов), для которого sec⁡y=x,|x|⩾1,0⩽y⩽π.{displaystyle sec y=x,qquad |x|geqslant 1,quad 0leqslant yleqslant pi .}

 

Функция y=arcsec⁡x{displaystyle y=operatorname {arcsec} x}

  непрерывна и ограничена на всей своей области определения. Она является строго возрастающей и всюду неотрицательной.

  • sec⁡(arcsec⁡x)=x{displaystyle sec(operatorname {arcsec} x)=x}  при |x|⩾1,{displaystyle |x|geqslant 1,} 
  • arcsec⁡(sec⁡y)=y{displaystyle operatorname {arcsec}(sec y)=y}  при 0⩽y⩽π.{displaystyle 0leqslant yleqslant pi .} 
  • D(arcsec⁡x)=(−∞;−1]∪[1,∞){displaystyle D(operatorname {arcsec} x)=(-infty ;-1]cup [1,infty )}  (область определения),
  • E(arcsec⁡x)=[0;π2)∪(π2;π]{displaystyle E(operatorname {arcsec} x)=[0;{frac {pi }{2}})cup ({frac {pi }{2}};pi ]}  (область значений).

Свойства функции arcsec

Функция arccosec

  График функции y=arccosec⁡x{displaystyle y=operatorname {arccosec} x} 

Арккосе́кансом числа x называется такое значение угла y (в радианной мере измерения углов), для которого cosec⁡y=x,|x|⩾1,−π/2⩽y⩽π/2.{displaystyle operatorname {cosec} y=x,qquad |x|geqslant 1,quad -pi /2leqslant yleqslant pi /2.}

 

Функция y=arccosec⁡x{displaystyle y=operatorname {arccosec} x}

  непрерывна и ограничена на всей своей области определения. Она является строго убывающей.

  • cosec⁡(arccosec⁡x)=x{displaystyle operatorname {cosec} (operatorname {arccosec} x)=x}  при |x|⩾1,{displaystyle |x|geqslant 1,} 
  • arccosec⁡(cosec⁡y)=y{displaystyle operatorname {arccosec} (operatorname {cosec} y)=y}  при −π/2⩽y⩽π/2.{displaystyle -pi /2leqslant yleqslant pi /2.} 
  • D(arccosec⁡x)=(−∞;−1]∪[1,∞){displaystyle D(operatorname {arccosec} x)=(-infty ;-1]cup [1,infty )}  (область определения),
  • E(arccosec⁡x)=[−π2;0)∪(0;π2]{displaystyle E(operatorname {arccosec} x)=[-{frac {pi }{2}};0)cup (0;{frac {pi }{2}}]}  (область значений).

Свойства функции arccosec

Разложение в ряды

  • arcsin⁡x=x+x36+3×540+⋯ =∑n=0∞(2n)!4n(n!)2(2n+1)x2n+1{displaystyle displaystyle arcsin x=x+{frac {x^{3}}{6}}+{frac {3x^{5}}{40}}+cdots =sum _{n=0}^{infty }{frac {(2n)!}{4^{n}(n!)^{2}(2n+1)}}x^{2n+1}}  для всех |x|≤1{displaystyle left|xright|leq 1} [4]
  • arccos⁡x=π2−arcsin⁡x=π2−∑n=0∞(2n)!4n(n!)2(2n+1)x2n+1{displaystyle displaystyle arccos x={pi over 2}-arcsin x={pi over 2}-sum _{n=0}^{infty }{frac {(2n)!}{4^{n}(n!)^{2}(2n+1)}}x^{2n+1}}  для всех |x|≤1{displaystyle left|xright|leq 1} 
  • arctg⁡ x=x−x33+x55−⋯ =∑n=1∞(−1)n−12n−1x2n−1{displaystyle displaystyle operatorname {arctg} x=x-{frac {x^{3}}{3}}+{frac {x^{5}}{5}}-cdots =sum _{n=1}^{infty }{frac {(-1)^{n-1}}{2n-1}}x^{2n-1}}  для всех |x|≤1{displaystyle left|xright|leq 1} 

Производные от обратных тригонометрических функций

Все обратные тригонометрические функции бесконечно дифференцируемы в каждой точке своей области определения. Первые производные:

(arcsin⁡x)′=11−x2.{displaystyle (arcsin x)’={frac {1}{sqrt {1-x^{2}}}}.}

 
(arccos⁡x)′=−11−x2.{displaystyle (arccos x)’=-{frac {1}{sqrt {1-x^{2}}}}.} 
(arctgx)′=1 1+x2.{displaystyle (operatorname {arctg} ,x)’={frac {1}{ 1+x^{2}}}.} 
(arcctgx)′=−1 1+x2.{displaystyle (operatorname {arcctg} ,x)’=-{frac {1}{ 1+x^{2}}}.} 
(arcsec⁡x)′=1|x|x2−1.{displaystyle (operatorname {arcsec} x)’={1 over |x|{sqrt {x^{2}-1}}}.} 
(arccosecx)′=−1|x|x2−1.{displaystyle (operatorname {arccosec} ,x)’=-{1 over |x|{sqrt {x^{2}-1}}}.} 

Интегралы от обратных тригонометрических функций

Неопределённые интегралы

Для действительных и комплексных x:

∫arcsin⁡xdx=xarcsin⁡x+1−x2+C,∫arccos⁡xdx=xarccos⁡x−1−x2+C,∫arctgxdx=xarctgx−12ln⁡(1+x2)+C,∫arcctgxdx=xarcctgx+12ln⁡(1+x2)+C,∫arcsec⁡xdx=xarcsec⁡x−ln⁡(x(1+x2−1×2))+C,∫arccosecxdx=xarccosecx+ln⁡(x(1+x2−1×2))+C.{displaystyle {begin{aligned}int arcsin x,dx&{}=x,arcsin x+{sqrt {1-x^{2}}}+C,int arccos x,dx&{}=x,arccos x-{sqrt {1-x^{2}}}+C,int operatorname {arctg} ,x,dx&{}=x,operatorname {arctg} ,x-{frac {1}{2}}ln left(1+x^{2}right)+C,int operatorname {arcctg} ,x,dx&{}=x,operatorname {arcctg} ,x+{frac {1}{2}}ln left(1+x^{2}right)+C,int operatorname {arcsec} x,dx&{}=x,operatorname {arcsec} x-ln left(xleft(1+{sqrt {{x^{2}-1} over x^{2}}},right)!right)+C,int operatorname {arccosec} ,x,dx&{}=x,operatorname {arccosec} ,x+ln left(xleft(1+{sqrt {{x^{2}-1} over x^{2}}},right)!right)+C.end{aligned}}} 

Для действительных x ≥ 1:

∫arcsec⁡xdx=xarcsec⁡x−ln⁡(x+x2−1)+C,∫arccosecxdx=xarccosecx+ln⁡(x+x2−1)+C.{displaystyle {begin{aligned}int operatorname {arcsec} x,dx&{}=x,operatorname {arcsec} x-ln left(x+{sqrt {x^{2}-1}}right)+C,int operatorname {arccosec} ,x,dx&{}=x,operatorname {arccosec} ,x+ln left(x+{sqrt {x^{2}-1}}right)+C.end{aligned}}} 
См. также Список интегралов от обратных тригонометрических функций

Использование в геометрии

  Прямоугольный треугольник ABC

Обратные тригонометрические функции используются для вычисления углов треугольника, если известны его стороны, например, с помощью теоремы косинусов.

В прямоугольном треугольнике эти функции от отношений сторон сразу дают угол.Так, если катет длины a{displaystyle a}

  является противолежащим для угла α{displaystyle alpha } , то

α=arcsin⁡(a/c)=arccos⁡(b/c)=arctg⁡(a/b)=arccosec⁡(c/a)=arcsec⁡(c/b)=arcctg⁡(b/a).{displaystyle alpha =arcsin(a/c)=arccos(b/c)=operatorname {arctg} (a/b)=operatorname {arccosec} (c/a)=operatorname {arcsec}(c/b)=operatorname {arcctg} (b/a).}

 

Связь с натуральным логарифмом

Для вычисления значений обратных тригонометрических функций от комплексного аргумента удобно использовать формулы, выражающие их через натуральный логарифм:

arcsin⁡z=−iln⁡(iz+1−z2)=π2−iln⁡(z+z2−1),{displaystyle {begin{aligned}arcsin z&{}=-iln(iz+{sqrt {1-z^{2}}})={frac {pi }{2}}-iln(z+{sqrt {z^{2}-1}}),end{aligned}}} 
arccos⁡z=π2+iln⁡(iz+1−z2),{displaystyle {begin{aligned}arccos z&{}={dfrac {pi }{2}}+iln(iz+{sqrt {1-z^{2}}}),end{aligned}}} 
arctgz=i2(ln⁡(1−iz)−ln⁡(1+iz)),{displaystyle {begin{aligned}operatorname {arctg} ,z&{}={dfrac {i}{2}}(ln(1-iz)-ln(1+iz)),end{aligned}}} 
arcctgz=i2(ln⁡(z−iz)−ln⁡(z+iz)),{displaystyle {begin{aligned}operatorname {arcctg} ,z&{}={dfrac {i}{2}}left(ln left({dfrac {z-i}{z}}right)-ln left({dfrac {z+i}{z}}right)right),end{aligned}}} 
arcsec⁡z=arccos⁡(z−1)=π2+iln⁡(1−1z2+iz),{displaystyle {begin{aligned}operatorname {arcsec} z&{}=arccos left(z^{-1}right)={dfrac {pi }{2}}+iln left({sqrt {1-{dfrac {1}{z^{2}}}}}+{dfrac {i}{z}}right),end{aligned}}} 
arccosecz=arcsin⁡(z−1)=−iln⁡(1−1z2+iz).{displaystyle {begin{aligned}operatorname {arccosec} ,z&{}=arcsin left(z^{-1}right)=-iln left({sqrt {1-{dfrac {1}{z^{2}}}}}+{dfrac {i}{z}}right).end{aligned}}} 

Примечания

  1. ↑ Александрова Н. В. История математических терминов, понятий, обозначений: Словарь-справочник, изд. 3-е. — СПб.: ЛКИ, 2008. — С. 211. — ISBN 978-5-382-00839-4.
  2. ↑ Здесь знак −1 определяет функцию x = f−1 (y), обратную функции y = f (x)
  3. ↑ Энциклопедический словарь, 1985, с. 220.
  4. ↑ При значении x, близком к 1, эта расчётная формула даёт большую погрешность. Поэтому можно воспользоваться формулой arcsin⁡x=arccos⁡1−x2,{displaystyle arcsin x=arccos {sqrt {1-x^{2}}},}  где arccos⁡x=π2−arcsin⁡x{displaystyle arccos x={pi over 2}-arcsin x} 

Ссылки

См. также

Читайте также