Гипотенуза (греч. ὑποτείνουσα, натянутая[1]) — самая длинная сторона прямоугольного треугольника, противоположная прямому углу. Длина гипотенузы прямоугольного треугольника может быть найдена с помощью теоремы Пифагора: квадрат длины гипотенузы равен сумме квадратов длин катетов.
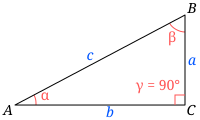Прямоугольный треугольник и его гипотенуза (c), а также катеты a и b
Например, если длина одного из катетов равна 3 м (квадрат его длины равен 9 м²), а длина другого — 4 м (квадрат его длины равен 16 м²), то сумма их квадратов равна 25 м². Длина гипотенузы в этом случае равна квадратному корню из 25 м², то есть 5 м.
Вычисление длины гипотенузы
Длину гипотенузы можно найти, применив теорему Пифагора.
Пусть a{displaystyle a}
и b{displaystyle b} — катеты, тогда гипотенузу можно найти по формуле:
и b{displaystyle b}
— катеты, тогда гипотенузу можно найти по формуле:- c=a2+b2{displaystyle c={sqrt {a^{2}+b^{2}}}} .
.В языке программирования Си:
#include <math.h>..c = sqrt(a*a + b*b);
В PHP:
$c = hypot ($a,$b);
В Паскале:
c := sqrt(a*a + b*b)
В Бейсике:
c = SQR(a*a + b*b)
В Python-е:
import mathc = math.sqrt(a*a + b*b)
В Java:
c = Math.sqrt(a * a + b * b)
Иногда в языке программирования для вычисления гипотенузы имеется функция от двух аргументов hypot(a, b), которая, однако может вызвать проблемы в случае, если в качестве аргументов заданы числа, которые не могут быть длинами катетов прямоугольного треугольника.
Если известна длина одного из катетов a{displaystyle a}
и угол, отличный от прямого, то можно найти длину гипотенузы по формулам:
- c=asinα{displaystyle c={frac {a}{sin alpha }}} для противолежащего угла α{displaystyle alpha } , и
для противолежащего угла α{displaystyle alpha }
, и- c=acosβ{displaystyle c={frac {a}{cos beta }}} для прилежащего угла β{displaystyle beta } .
для прилежащего угла β{displaystyle beta }
.См. также
Примечания
- ↑ Александрова Н. В. Математические термины.(справочник). М.: Высшая школа, 1978, с. 26.
