У этого термина существуют и другие значения, см. Граф (значения).
Граф — математическая абстракция реальной системы объектов любой природы, обладающих парными связями.Граф как математический объект есть совокупность двух множеств — множества самих объектов, называемого множеством вершин и множеством их парных связей, называемой множеством рёбер. Элемент множества рёбер есть пара элементов множества вершин.
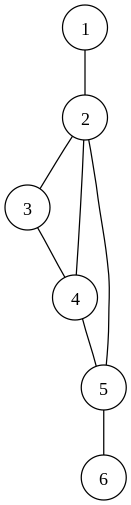 Неориентированный граф с шестью вершинами и семью рёбрами
Неориентированный граф с шестью вершинами и семью рёбрами
Графы находят широкое применение в современной науке и технике. Они используются и в естественных науках (физике и химии) и в социальных науках (например, социологии), но наибольших масштабов применение графов получило в информатике и сетевых технологиях.
В качестве простейшего примера из жизни можно привести схему перелётов определённой авиакомпании, которая моделируется графом, где вершинами графа являются города, а рёбрами — рейсы, соединяющие пары городов. Дерево каталогов в компьютере также является графом: диски, папки и файлы являются вершинами, а рёбра показывают вложенность файлов и папок в папки и диски[1].
Для разных областей применения виды графов могут различаться направленностью, ограничениями на количество связей и дополнительными данными о вершинах или рёбрах.Многие структуры в математике и информатике, представляющие практический интерес, могут быть представлены графами. Например, строение Википедии моделируется ориентированного графа, в котором вершины — статьи, а дуги (ориентированные рёбра) — гиперссылки (тематическая карта).
Графы являются основным объектом изучения теории графов.
Содержание
- 1 Определения
- 2 Обобщение понятия графа
- 3 Способы представления графа в информатике
- 4 См. также
- 5 Примечания
- 6 Литература
Определения
Основная статья: Глоссарий теории графов
Реальные системы, элементы которых обладают парными связями достаточно разнообразны, и описывающие их абстракции — графы также бывают различных типов. Простейшей абстракцией таких систем является простой граф.
Простой Граф
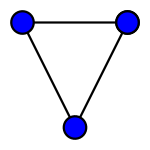 Пример диаграммы неориентированного графа
Пример диаграммы неориентированного графа
Определение. Простой граф G(V,E){displaystyle G(V,E)}
есть совокупность двух множеств – непустого множества V{displaystyle V} и множества E{displaystyle E} неупорядоченных пар различных элементов множества V{displaystyle V} . Множество V{displaystyle V} называется множеством вершин, множество E{displaystyle E} называется множеством рёбер
- G(V,E)=⟨V,E⟩,V≠∅,E∈V×V,{v,v}∉E,v∈V{displaystyle G(V,E)=leftlangle V,Erightrangle ,quad Vneq varnothing ,quad Ein Vtimes V,quad left{v,vright}notin E,quad vin V} ,
то есть множество E{displaystyle E}
состоит из 2-элементных подмножеств множества V{displaystyle V} .
Сопутствующие термины
Теория графов не обладает устоявшейся терминологией. Поэтому в некоторых публикациях могут использоваться термины, отличные от приведенных ниже.
- Вершина (узел, точка) (англ. vertex, node, point) графа G{displaystyle G} есть элемент множества вершин v∈V(G){displaystyle vin V(G)} ;
- Ребро (линия) (англ. edge, line) графа G{displaystyle G} есть элемент множества ребер e∈E(G){displaystyle ein E(G)} , или e={v1,v2}{displaystyle e=left{v_{1},v_{2}right}} , где v1∈V(G),v2∈V(G){displaystyle v_{1}in V(G),quad v_{2}in V(G)} ;
- Элементами графа G{displaystyle G} называются его вершины v∈V(G){displaystyle vin V(G)} и рёбра e∈E(G){displaystyle ein E(G)} графа;
- Порядок (англ. order) графа G{displaystyle G} есть кардинальное число множества вершин n=|V(G)|{displaystyle n=|V(G)|} или, другими словами, количество вершин;
- Размер (англ. size) графа G{displaystyle G} есть кардинальное число множества ребер m=|E(G)|{displaystyle m=|E(G)|} или, другими словами, количество ребер;
- Вершина v{displaystyle v} инцидентна (англ. incident) ребру e{displaystyle e} , если v∈e{displaystyle vin e} ; тогда еще говорят, что e{displaystyle e} есть ребро при v{displaystyle v} ;
- Концевые вершины (концы) (англ. endvertices, ends) есть две вершины, инцидентные ребру. Ребро соединяет (англ. joins) свои концевые вершины;
- Соседние (смежные) вершины (англ. neighbours, adjacent) есть такие вершины v1{displaystyle v_{1}} и v2{displaystyle v_{2}} что {v1,v2}∈E(G){displaystyle left{v_{1},v_{2}right}in E(G)} или, другими, словами обе вершины являются концевыми для одного ребра;
- Смежные ребра (англ. adjacent edges) это ребра, инцидентные одной вершине или e1={v,v1}{displaystyle e_{1}=left{v,v_{1}right}} и e2={v,v2}{displaystyle e_{2}=left{v,v_{2}right}} — смежные;
- Степень (валентность) вершины (англ. degree, valency) есть количество инцидентных ей рёбер. Степень вершины обозначается как d(v){displaystyle d(v)} ;
- Изолированной вершиной (англ. isolated) называется вершина со степенью d(v)=0{displaystyle d(v)=0} , то есть не является концом ни для одного ребра;
- Висячей вершиной (листом) (англ. leaf) называется вершина со степенью d(v)=1{displaystyle d(v)=1} , то есть которая является концом ровно одного ребра.
Обычно граф изображают диаграммой: вершины – точками, ребра – линиями.
Псевдограф
Псевдограф G(V,E){displaystyle G(V,E)}
есть совокупность двух множеств – непустого множества V{displaystyle V} и множества E{displaystyle E} неупорядоченных пар элементов множества V{displaystyle V} .
- G(V,E)=⟨V,E⟩,V≠∅,E∈V×V{displaystyle G(V,E)=leftlangle V,Erightrangle ,quad Vneq varnothing ,quad Ein Vtimes V}
В множестве ребер псевдографа разрешен элемент {v,v}∈E(G){displaystyle left{v,vright}in E(G)}
.
- Петлей (англ. loop) называется элемент e={v,v}{displaystyle e=left{v,vright}} , являющийся ребром у которого концевые вершины совпадают.
Другими словами если элементами множества E могут быть петли, то граф называется псевдографом [2].
Мультиграф
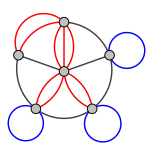 Псевдомультиграф с кратными рёбрами (красные) и петлями (синие).
Псевдомультиграф с кратными рёбрами (красные) и петлями (синие).
Мультиграф G(V,E){displaystyle G(V,mathbf {E} )}
есть совокупность двух множеств – непустого множества V{displaystyle V} и мультимножества E{displaystyle mathbf {E} } неупорядоченных пар различных элементов множества V{displaystyle V} .
- G(V,E)=⟨V,E⟩,V≠∅,E∈V×V{v,v}∉E,v∈V{displaystyle G(V,mathbf {E} )=leftlangle V,mathbf {E} rightrangle ,quad Vneq varnothing ,quad mathbf {E} in Vtimes Vquad left{v,vright}notin mathbf {E} ,quad vin V}
- Кратными ребрами называются одинаковые элементы мультимножества {e,e,…,e}∈E{displaystyle left{e,e,dots ,eright}in mathbf {E} } , то есть ребра, чьи концевые вершины совпадают.
Другими словами Если E{displaystyle E}
не множество, а семейство, то есть если E{displaystyle mathbf {E} } содержит одинаковые элементы, то такие элементы называются кратными рёбрами, а граф называется мультиграфом [2].
Псевдомультиграф
Псевдомультиграф G(V,E){displaystyle G(V,mathbf {E} )}
есть совокупность двух множеств – непустого множества V{displaystyle V} и мультимножества E{displaystyle mathbf {E} } неупорядоченных пар элементов множества V{displaystyle V} .
- G(V,E)=⟨V,E⟩,V≠∅,E∈V×V{displaystyle G(V,mathbf {E} )=leftlangle V,mathbf {E} rightrangle ,quad Vneq varnothing ,quad mathbf {E} in Vtimes V}
Другими словами Если E{displaystyle mathbf {E} }
семейство содержащее одинаковые элементы (кратные ребра) и E{displaystyle mathbf {E} } может содержать петли, то граф называется псевдомультиграфом[2].
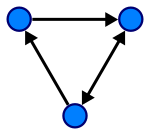
Ориентированный граф
Ориентированный граф (орграф) (англ. directed graph or dirgaph) G(V,E){displaystyle G(V,E)}
есть совокупность двух множеств – непустого множества V{displaystyle V} и множества E{displaystyle E} дуг или упорядоченных пар различных элементов множества V{displaystyle V}
- G(V,E)=⟨V,E⟩,V≠∅,⟨{v1,v2},≺⟩∈E,v∈V{displaystyle G(V,E)=leftlangle V,Erightrangle ,quad Vneq varnothing ,quad leftlangle left{v_{1},v_{2}right},prec rightrangle in E,quad vin V} .
совместно с двумя отображениями
- init:E→V,ter:E→V{displaystyle init:Erightarrow V,quad ter:Erightarrow V} ,
где отображение init:E→V{displaystyle init:Erightarrow V}
ставит в соответствие каждой дуге ее начальную вершину (начало дуги) init(e){displaystyle init(e)} , а отображение ter:E→V{displaystyle ter:Erightarrow V} ставит в соответствие каждой дуге ее конечную вершину (конец дуги) ter(e){displaystyle ter(e)} . Говорят что дуга e{displaystyle e} ведет из init(e){displaystyle init(e)} в ter(e){displaystyle ter(e)}
Смешанный граф
Основная статья: Смешанный граф
Смешанный граф (англ. Mixed graph) G(V,E,U){displaystyle G(V,E,U)}
— это совокупность трех множеств – непустого множества вершин V{displaystyle V} , и множества дуг E{displaystyle E} или упорядоченных пар различных элементов множества V{displaystyle V} и множества ребер U{displaystyle U} неупорядоченных пар различных элементов множества V{displaystyle V}
- G(V,E,U)=⟨V,E,U⟩,V≠∅,⟨{v1,v2},≺⟩∈E,{v3,v4}∈U,v∈V{displaystyle G(V,E,U)=leftlangle V,E,Urightrangle ,quad Vneq varnothing ,quad leftlangle left{v_{1},v_{2}right},prec rightrangle in E,quad left{v_{3},v_{4}right}in U,quad vin V} .
совместно с двумя отображениями
- init:E→V,ter:E→V{displaystyle init:Erightarrow V,quad ter:Erightarrow V}
Ориентированный и неориентированный графы являются частными случаями смешанного.
Изоморфные графы
Граф G{displaystyle G}
называется изоморфным графу H{displaystyle H} , если существует биекция f{displaystyle f} из множества вершин графа G{displaystyle G} в множество вершин графа H{displaystyle H} , обладающая следующим свойством: если в графе G{displaystyle G} есть ребро из вершины A{displaystyle A} в вершину B{displaystyle B} , то в графе H{displaystyle H} должно быть ребро из вершины f(A){displaystyle f(A)} в вершину f(B){displaystyle f(B)} и наоборот — если в графе H{displaystyle H} есть ребро из вершины A{displaystyle A} в вершину B{displaystyle B} , то в графе G{displaystyle G} должно быть ребро из вершины f−1(A){displaystyle f^{-1}(A)} в вершину f−1(B){displaystyle f^{-1}(B)} . В случае ориентированного графа эта биекция также должна сохранять ориентацию ребра. В случае взвешенного графа биекция также должна сохранять вес ребра.
Прочие связанные определения
Маршрутом в графе называют конечную последовательность вершин, в которой каждая вершина (кроме последней) соединена со следующей в последовательности вершиной ребром. Цепью называется маршрут без повторяющихся рёбер. Простой цепью называется маршрут без повторяющихся вершин (откуда следует, что в простой цепи нет повторяющихся рёбер).
Ориентированным маршрутом (или путём) в орграфе называют конечную последовательность вершин и дуг, в которой каждый элемент инцидентен предыдущему и последующему.
Циклом называют цепь, в которой первая и последняя вершины совпадают. При этом длиной пути (или цикла) называют число составляющих его рёбер. Заметим, что если вершины u{displaystyle u}
и v{displaystyle v} являются концами некоторого ребра, то согласно данному определению, последовательность (u,v,u){displaystyle (u,v,u)} является циклом. Чтобы избежать таких «вырожденных» случаев, вводят следующие понятия.
Путь (или цикл) называют простым, если рёбра в нём не повторяются; элементарным, если он простой и вершины в нём не повторяются.
Простейшие свойства путей и циклов:
- всякий путь, соединяющий две вершины, содержит элементарный путь, соединяющий те же две вершины;
- всякий простой неэлементарный путь содержит элементарный цикл;
- всякий простой цикл, проходящий через некоторую вершину (или ребро), содержит элементарный (под-)цикл, проходящий через ту же вершину (или ребро);
- петля — элементарный цикл.
Бинарное отношение на множестве вершин графа, заданное как «существует путь из u{displaystyle u}
в v{displaystyle v} », является отношением эквивалентности и, следовательно, разбивает это множество на классы эквивалентности, называемые компонентами связности графа. Если у графа ровно одна компонента связности, то граф связный. На компоненте связности можно ввести понятие расстояния между вершинами как минимальную длину пути, соединяющего эти вершины.
Всякий максимальный связный подграф графа G{displaystyle G}
называется связной компонентой (или просто компонентой) графа G{displaystyle G} . Слово «максимальный» означает максимальный относительно включения, то есть не содержащийся в связном подграфе с большим числом элементов.
Ребро графа называется мостом, если его удаление увеличивает число компонент.
Дополнительные характеристики графов
Граф называется:
- связным, если для любых вершин u{displaystyle u} ,v{displaystyle v} есть путь из u{displaystyle u} в v{displaystyle v} .
- сильно связным или ориентированно связным, если он ориентированный, и из любой вершины в любую другую имеется ориентированный путь.
- деревом, если он связный и не содержит нетривиальных циклов.
- полным, если любые его две (различные, если не допускаются петли) вершины соединены ребром.
- двудольным, если его вершины можно разбить на два непересекающихся подмножества V1{displaystyle V_{1}} и V2{displaystyle V_{2}} так, что всякое ребро соединяет вершину из V1{displaystyle V_{1}} с вершиной из V2{displaystyle V_{2}} .
- k-дольным, если его вершины можно разбить на k{displaystyle k} непересекающихся подмножеств V1{displaystyle V_{1}} , V2{displaystyle V_{2}} , …, Vk{displaystyle V_{k}} так, что не будет рёбер, соединяющих вершины одного и того же подмножества.
- полным двудольным, если каждая вершина одного подмножества соединена ребром с каждой вершиной другого подмножества.
- планарным, если граф можно изобразить диаграммой на плоскости без пересечений рёбер.
- взвешенным, если каждому ребру графа поставлено в соответствие некоторое число, называемое весом ребра.
- хордальным, если граф не содержит индуцированных циклов с длиной больше трёх.
Также бывает:
Обобщение понятия графа
Простой граф является одномерным симплициальным комплексом.
Более абстрактно, граф можно задать как тройку (V,E,φ){displaystyle (V,E,varphi )}
,где V{displaystyle V} и E{displaystyle E} — некоторые множества (вершин и рёбер, соотв.),а φ{displaystyle varphi } — функция инцидентности (или инцидентор), сопоставляющая каждому ребруe∈E{displaystyle ein E} (упорядоченную или неупорядоченную) пару вершин u{displaystyle u} и v{displaystyle v} из V{displaystyle V} (его концов). Частными случаями этого понятия являются:
- ориентированные графы (орграфы) — когда φ(e){displaystyle varphi (e)} всегда является упорядоченной парой вершин;
- неориентированные графы — когда φ(e){displaystyle varphi (e)} всегда является неупорядоченной парой вершин;
- смешанные графы — граф, в котором встречаются как ориентированные, так и неориентированные рёбра и петли;
- эйлеровы графы — граф, в котором существует циклический эйлеров путь (эйлеров цикл);
- мультиграфы — графы с кратными рёбрами, имеющими своими концами одну и ту же пару вершин;
- псевдографы — это мультиграфы, допускающие наличие петель;
- простые графы — не имеющие петель и кратных рёбер.
Под данное выше определение не подходят некоторые другие обобщения:
- гиперграф — если ребро может соединять более двух вершин.
- ультраграф — если между элементами xi{displaystyle x_{i}} и uj{displaystyle u_{j}} существуют бинарные отношения инцидентности.
Способы представления графа в информатике
Матрица смежности
Основная статья: Матрица смежности
Таблица, где как столбцы, так и строки соответствуют вершинам графа.В каждой ячейке этой матрицы записывается число, определяющее наличие связи от вершины-строки к вершине-столбцу (либо наоборот).
Это наиболее удобный способ представления плотных графов.
Недостатком являются требования к памяти, прямо пропорциональные квадрату количества вершин.
- Двумерный массив;
- Матрица с пропусками;
- Неявное задание (при помощи функции).
Матрица инцидентности
Основная статья: Матрица инцидентности
Таблица, где строки соответствуют вершинам графа, а столбцы соответствуют связям (рёбрам) графа.В ячейку матрицы на пересечении строки i{displaystyle i}
со столбцом j{displaystyle j} записывается:
- 1
- в случае, если связь j{displaystyle j} «выходит» из вершины i{displaystyle i} ,
- −1,
- если связь «входит» в вершину,
- 0
- во всех остальных случаях (то есть если связь является петлёй или связь не инцидентна вершине)
Данный способ является довольно ёмким (размер пропорционален |V||E|{displaystyle |V||E|}
) для хранения, поэтому применяется очень редко, в особых случаях (например, для быстрого нахождения циклов в графе).
Список смежности
Основная статья: Список смежности
Список, где каждой вершине графа соответствует строка, в которой хранится список смежных вершин. Такая структура данных не является таблицей в обычном понимании, а представляет собой «список списков».
Размер занимаемой памяти: O(|V|+|E|){displaystyle O(|V|+|E|)}
.
Это наиболее удобный способ для представления разреженных графов, а также при реализации базовых алгоритмов обхода графа в ширину или глубину, где нужно быстро получать «соседей» текущей просматриваемой вершины.
Список рёбер
Список, где каждому ребру графа соответствует строка, в которой хранятся две вершины, инцидентные ребру.
Размер занимаемой памяти: O(|E|){displaystyle O(|E|)}
.
Это наиболее компактный способ представления графов, поэтому часто применяется для внешнего хранения или обмена данными.
Языки описания и программы построения графов
Языки описания
Для описания графов, пригодного для машинной обработки и одновременно удобного для человеческого восприятия, используется несколько стандартизированных языков, среди которых:
Программы для построения
Разработана серия коммерческих программ для построения графов, так, построение графов лежит в основе прикладных программных пакетов фирмы ILOG (с 2009 года принадлежит корпорации IBM), среди других программ — GoView, Lassalle AddFlow, LEDA (есть бесплатная редакция).
Также существует свободная программа для построения графов igraph и свободная библиотека Boost.
Программы для визуализации
Для визуализации графов применяются следующие программные средства:
- Graphviz (Eclipse Public License)
- LION Graph Visualizer.
- Графоанализатор — русскоязычная программа, с простым пользовательским интерфейсом (GNU LGPL; только для Windows).
- Gephi — графическая оболочка для представления и изучения графов (GNU GPL, CDDL).
- Библиотека GraphX — свободная библиотека для .NET для расчёта и отрисовки графов, использует WPF 4.0.
- Библиотека MSAGL — свободная библиотека для .NET[3].
См. также
Примечания
- ↑ Буркатовская, 2014, с. 3.
- ↑ 1 2 3 Буркатовская, 2014, с. 6.
- ↑ Microsoft Automatic Graph Layout — Microsoft Research (неопр.). research.microsoft.com. Дата обращения: 15 ноября 2015.
Литература
- Буркатовския Ю. Б. Теория графов. — Томск: Издательство Томского политехнического университета, 2014. — Т. 1. — 200 с.
- Дистель Р. Теория графов. — Новосибирск: Издательство Института математики им. С. Л. Соболева СО РАН, 2002. — 336 с. — ISBN 5-86134-101-Х.
- Емеличев В. А., Мельников О. И., Сарванов В. И., Тышкевич Р. И. Лекции по теории графов. М.: Наука, 1990. 384с. (Изд.2, испр. М.: УРСС, 2009. 392 с.)
- Касьянов В. Н., Евстигнеев В.А. Графы в программировании: обработка, визуализация и применение. — СПб.: БХВ-Петербург, 2003. — С. 1104. — ISBN 5-94157-184-4.
- Кирсанов М. Н. Графы в Maple. — М.: Физматлит, 2007. — 168 с. — ISBN 978-5-9221-0745-7.
- Кормен Т. М. и др. Часть VI. Алгоритмы для работы с графами // Алгоритмы: построение и анализ = Introduction to Algorithms. — 2-е изд. — М.: Вильямс, 2006. — С. 1296. — ISBN 0-07-013151-1.
- Оре О. Теория графов. — М.: Наука, 1968. — 336 с.
- Графы // Энциклопедический словарь юного математика / Сост. А. П. Савин. — М.: Педагогика, 1985. — С. 86-88. — 352 с.
- Салий В. Н., Богомолов А. М. Алгебраические основы теории дискретных систем. — М.: Физико-математическая литература, 1997. — ISBN 5-02-015033-9.
- Уилсон Р. Введение в теорию графов. — М.: Мир, 1977. — 208 с.
- Харари Ф. Теория графов. — М.: Мир, 1973.
Для улучшения этой статьи желательно:
После исправления проблемы исключите её из списка. Удалите шаблон, если устранены все недостатки. |

 есть совокупность двух множеств – непустого множества V{displaystyle V}
есть совокупность двух множеств – непустого множества V{displaystyle V} и множества E{displaystyle E}
и множества E{displaystyle E} неупорядоченных пар различных элементов множества V{displaystyle V}
неупорядоченных пар различных элементов множества V{displaystyle V} ,
, есть элемент множества вершин v∈V(G){displaystyle vin V(G)}
есть элемент множества вершин v∈V(G){displaystyle vin V(G)} ;
; , или e={v1,v2}{displaystyle e=left{v_{1},v_{2}right}}
, или e={v1,v2}{displaystyle e=left{v_{1},v_{2}right}} , где v1∈V(G),v2∈V(G){displaystyle v_{1}in V(G),quad v_{2}in V(G)}
, где v1∈V(G),v2∈V(G){displaystyle v_{1}in V(G),quad v_{2}in V(G)} ;
; или, другими словами, количество вершин;
или, другими словами, количество вершин; или, другими словами, количество ребер;
или, другими словами, количество ребер; инцидентна (
инцидентна ( , если v∈e{displaystyle vin e}
, если v∈e{displaystyle vin e} ; тогда еще говорят, что e{displaystyle e}
; тогда еще говорят, что e{displaystyle e} и v2{displaystyle v_{2}}
и v2{displaystyle v_{2}} что {v1,v2}∈E(G){displaystyle left{v_{1},v_{2}right}in E(G)}
что {v1,v2}∈E(G){displaystyle left{v_{1},v_{2}right}in E(G)} или, другими, словами обе вершины являются концевыми для одного ребра;
или, другими, словами обе вершины являются концевыми для одного ребра; и e2={v,v2}{displaystyle e_{2}=left{v,v_{2}right}}
и e2={v,v2}{displaystyle e_{2}=left{v,v_{2}right}} — смежные;
— смежные; ;
; , то есть не является концом ни для одного ребра;
, то есть не является концом ни для одного ребра; , то есть которая является концом ровно одного ребра.
, то есть которая является концом ровно одного ребра.
 .
. , являющийся ребром у которого концевые вершины совпадают.
, являющийся ребром у которого концевые вершины совпадают. есть совокупность двух множеств – непустого множества V{displaystyle V}
есть совокупность двух множеств – непустого множества V{displaystyle V} неупорядоченных пар различных элементов множества V{displaystyle V}
неупорядоченных пар различных элементов множества V{displaystyle V}
 , то есть ребра, чьи концевые вершины совпадают.
, то есть ребра, чьи концевые вершины совпадают.
 .
. ,
, ставит в соответствие каждой дуге ее начальную вершину (начало дуги) init(e){displaystyle init(e)}
ставит в соответствие каждой дуге ее начальную вершину (начало дуги) init(e){displaystyle init(e)} , а отображение ter:E→V{displaystyle ter:Erightarrow V}
, а отображение ter:E→V{displaystyle ter:Erightarrow V} ставит в соответствие каждой дуге ее конечную вершину (конец дуги) ter(e){displaystyle ter(e)}
ставит в соответствие каждой дуге ее конечную вершину (конец дуги) ter(e){displaystyle ter(e)} . Говорят что дуга e{displaystyle e}
. Говорят что дуга e{displaystyle e} — это совокупность трех множеств – непустого множества вершин V{displaystyle V}
— это совокупность трех множеств – непустого множества вершин V{displaystyle V} неупорядоченных пар различных элементов множества V{displaystyle V}
неупорядоченных пар различных элементов множества V{displaystyle V} .
. , если существует
, если существует  из множества вершин графа G{displaystyle G}
из множества вершин графа G{displaystyle G} в вершину B{displaystyle B}
в вершину B{displaystyle B} , то в графе H{displaystyle H}
, то в графе H{displaystyle H} в вершину f(B){displaystyle f(B)}
в вершину f(B){displaystyle f(B)} и наоборот — если в графе H{displaystyle H}
и наоборот — если в графе H{displaystyle H} в вершину f−1(B){displaystyle f^{-1}(B)}
в вершину f−1(B){displaystyle f^{-1}(B)} . В случае
. В случае  и v{displaystyle v}
и v{displaystyle v} является циклом. Чтобы избежать таких «вырожденных» случаев, вводят следующие понятия.
является циклом. Чтобы избежать таких «вырожденных» случаев, вводят следующие понятия. и V2{displaystyle V_{2}}
и V2{displaystyle V_{2}} так, что всякое ребро соединяет вершину из V1{displaystyle V_{1}}
так, что всякое ребро соединяет вершину из V1{displaystyle V_{1}} непересекающихся подмножеств V1{displaystyle V_{1}}
непересекающихся подмножеств V1{displaystyle V_{1}} так, что не будет рёбер, соединяющих вершины одного и того же подмножества.
так, что не будет рёбер, соединяющих вершины одного и того же подмножества. ,где V{displaystyle V}
,где V{displaystyle V} — функция инцидентности (или инцидентор), сопоставляющая каждому ребруe∈E{displaystyle ein E}
— функция инцидентности (или инцидентор), сопоставляющая каждому ребруe∈E{displaystyle ein E} (упорядоченную или неупорядоченную) пару вершин u{displaystyle u}
(упорядоченную или неупорядоченную) пару вершин u{displaystyle u} всегда является упорядоченной парой вершин;
всегда является упорядоченной парой вершин; и uj{displaystyle u_{j}}
и uj{displaystyle u_{j}} существуют бинарные отношения
существуют бинарные отношения  со столбцом j{displaystyle j}
со столбцом j{displaystyle j} записывается:
записывается: ) для хранения, поэтому применяется очень редко, в особых случаях (например, для быстрого нахождения циклов в графе).
) для хранения, поэтому применяется очень редко, в особых случаях (например, для быстрого нахождения циклов в графе). .
. .
.