Алгебраическая кривая или плоская алгебраическая кривая— это геометрическое место (множество) точек на плоскости (O;x,y), которое определяется как множество нулей многочлена от двух переменных. Степенью (или порядком) n этой кривой называется степень этого многочлена. Алгебраические кривые степеней n = 1, 2, 3, … , 8 кратко называются прямыми, кониками, куби́ками, квартиками, пентиками, секстиками, септиками, октиками соответственно. Например, единичная окружность — это алгебраическая кривая степени 2 (коника), так как она задаётся уравнением x2 + y2 − 1 = 0.
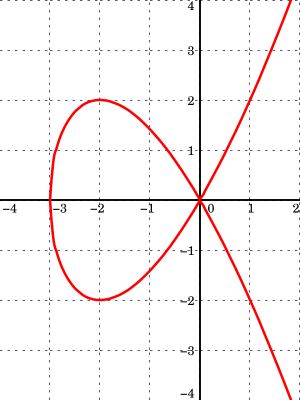 Куби́ка Чирнгауза — алгебраическая кривая третьего порядка.
Куби́ка Чирнгауза — алгебраическая кривая третьего порядка.
По многим техническим причинам удобно рассматривать не только вещественные, но и комплексные корни соответствующего многочлена, а также обобщить определение на случай произвольного основного поля.
В алгебраической геометрии, плоская аффинная алгебраическая кривая над полем k определяется как множество точек K2, являющихся корнями многочлена от двух переменных с коэффицентами в k, где K — алгебраическое замыкание поля k. Точки этой кривой, все координаты которых лежат в k, называются k-точками. Например, точка (2,−3){displaystyle (2,{sqrt {-3}})} принадлежит рассмотренной выше единичной окружности, однако не принадлежит её действительной части. Многочлен x2 + y2 + 1 задаёт алгебраическую кривую, действительная часть которой пуста.
принадлежит рассмотренной выше единичной окружности, однако не принадлежит её действительной части. Многочлен x2 + y2 + 1 задаёт алгебраическую кривую, действительная часть которой пуста.
Более общо, можно рассматривать алгебраические кривые, содержащиеся не в плоскости, а в пространстве с большим числом измерений или в проективном пространстве. Оказывается, что многие свойства алгебраической кривой не зависят от выбора конкретного вложения в некоторое пространство, и это приводит к общему определению алгебраической кривой:
Алгебраическая кривая — это алгебраическое многообразие размерности 1. Это определение можно переформулировать так: алгебраическая кривая — это алгебраическое многообразие, все алгебраические подмногообразия которого состоят из одной точки.
Содержание
Примеры алгебраических кривых
Рациональные кривые
Рациональная кривая, также известная как уникурсальная кривая, — это кривая, бирационально эквивалентная аффинной прямой (или проективной прямой?!), другими словами, кривая, допускающая рациональную параметризацию.
Более конкретно, рациональная кривая в n-мерном пространстве может быть параметризована (за исключением некоторого числа изолированных «особых точек») при помощи n рациональных функций от единственного параметра t.
Любое коническое сечение над полем рациональных чисел, содержащее хотя бы одну рациональную точку, является рациональной кривой.[1] Её можно параметризовать, проведя через рациональную точку прямую с произвольным угловым коэффициентом t и сопоставив данному t вторую точку пересечения прямой и коники (их не может быть больше двух).
 x2 + xy + y2 = 1
x2 + xy + y2 = 1
Например, рассмотрим эллипс x2 + xy + y2 = 1 с рациональной точкой (−1, 0). Проведя через неё прямую y = t(x + 1), подставив выражение y через x в уравнение и решив относительно x, получим уравнения
- x=1−t21+t+t2,{displaystyle x={frac {1-t^{2}}{1+t+t^{2}}},}

- y=t(x+1)=t(t+2)1+t+t2,{displaystyle y=t(x+1)={frac {t(t+2)}{1+t+t^{2}}},,}

задающие рациональную параметризацию эллипса. В таком виде представимы все точки эллипса кроме точки (−1, 0), можно сопоставить ей t = ∞, то есть параметризовать эллипс проективной прямой.
Эту рациональную параметризацию можно рассматривать как параметризацию «эллипса в проективном пространстве», перейдя к однородным координатам, то есть заменив t на T/U, а x, y — на X/Z, Y/Z соответственно. Параметризация эллипса X2 + XY + Y2 = Z2 проективной прямой примет следующий вид:
- X=U2−T2,Y=T(T+2U),Z=T2+TU+U2.{displaystyle X=U^{2}-T^{2},quad Y=T,(T+2,U),quad Z=T^{2}+TU+U^{2}.}

Эллиптические кривые
Рациональные кривые (над алгебраически замкнутым полем) — это в точности алгебраические кривые рода 0 (см. ниже), в этой терминологии эллиптические кривые — это кривые рода 1 с рациональной точкой. Любая такая кривая может быть представлена как куби́ка без особенностей.
Эллиптическая кривая несёт на себе структуру абелевой группы. Сумма трёх точек на куби́ке равна нулю тогда и только тогда, когда эти точки коллинеарны.
Пересечение двух коник является кривой четвёртого порядка рода 1, а значит, эллиптической кривой, если содержит хотя бы одну рациональную точку. В противном случае пересечение может быть рациональной кривой четвёртого порядка с особеннностями, или быть разложимым на кривые меньшего порядка (кубика и прямая, две коники, коника и две прямые или четыре прямые).
Связь с полями функций
Изучение алгебраических кривых может быть сведено к изучению неприводимых кривых (то есть не раскладывающихся в объединение двух меньших кривых). Каждой такой кривой можно сопоставить поле рациональных функций на ней; оказывается, что кривые бирационально эквивалентны тогда и только тогда, когда их поля функций изоморфны. Это значит, что категория алгебраических кривых и рациональных отображений двойственна категории одномерных полей алгебраических функций, то есть полей, являющихся алгебраическими расширениями поля k(x){displaystyle k(x)}
 .
.
Комплексные кривые как действительные поверхности
Комплексная алгебраическая кривая, вложенная в аффинное или проективное пространство, имеет топологическую размерность 2, другими словами, является поверхностью. В частности, комплексная алгебраическая кривая без особенностей является двумерным ориентируемым многообразием.
Топологический род этой поверхности совпадает с родом алгебраической кривой (который можно вычислить алгебраическими способами). Если проекция кривой без особенностей на плоскость является алгебраической кривой степени d с простейшими особенностями (обыкновенными двойными точками), то исходная кривая имеет род (d − 1)(d − 2)/2 − k, где k — число этих особенностей.
Изучение компактных римановых поверхностей состоит фактически в изучении комплексных алгебраических кривых без особенностей, рассматриваемых как поверхности с дополнительной аналитической структурой. Более точно, следующие категории эквивалентны:
Классификация особенностей
 x3 − y2 = 0
x3 − y2 = 0
Особые точки включают в себя несколько типов точек, в которых кривая «пересекает сама себя», а также различные типы каспов. Например, на рисунке показана кривая x3 − y2 = 0 с каспом в начале координат.
Особые точки можно классифицировать по их инвариантам. Например, особую точку с дельта-инвариантом δ можно интуитивно описать как точку, в которой встречаются сразу δ «самопересечений». В случае точки P на неприводимой кривой δ можно вычислить как длину модуля OP~/OP{displaystyle {widetilde {{mathcal {O}}_{P}}}/{mathcal {O}}_{P}}
 , где OP{displaystyle {mathcal {O}}_{P}}
, где OP{displaystyle {mathcal {O}}_{P}} — локальное кольцо в точке P и OP~{displaystyle {widetilde {{mathcal {O}}_{P}}}}
— локальное кольцо в точке P и OP~{displaystyle {widetilde {{mathcal {O}}_{P}}}} — его целое замыкание. Вычисление дельта-инвариантов всех особых точек позволяет вычислить род кривой по формуле:
— его целое замыкание. Вычисление дельта-инвариантов всех особых точек позволяет вычислить род кривой по формуле:
- g=12(d−1)(d−2)−∑PδP,{displaystyle g={frac {1}{2}}(d-1)(d-2)-sum _{P}delta _{P},}

Другие важные инварианты: кратность m особенности (максимальное целое число, такое что все производные задающего кривую многочлена, порядок которых не превосходит m, равны нулю) и число Милнора[en].
См. также
Примечания
- ↑ Ю. И. Манин. Рациональные точки на алгебраических кривых. — Успехи математических наук, т. XIX, вып. 6 (120), 1964.
Литература
- Ж.-П. Серр. Алгебраические группы и поля классов. — М.: Мир, 1968. — 285 с.
- Джон Милнор. Особые точки комплексных гиперповерхностей. — М.: Мир, 1971. — 121 с.
- Egbert Brieskorn, Horst Knörrer. Plane Algebraic Curves. — Birkhäuser, 1986.
- Hershel M. Farkas, Irwin Kra. Riemann Surfaces. — Springer, 1980.
- W. Fulton. Algebraic Curves: an introduction to algebraic geometry.
- C.G. Gibson. Elementary Geometry of Algebraic Curves: An Undergraduate Introduction. — Cambridge University Press, 1998.
Не следует путать с Эллипс.
Эллипти́ческая крива́я над полем K{displaystyle K} — неособая кубическая кривая на проективной плоскости над K^{displaystyle {hat {K}}}
— неособая кубическая кривая на проективной плоскости над K^{displaystyle {hat {K}}} (алгебраическим замыканием поля K{displaystyle K}
(алгебраическим замыканием поля K{displaystyle K} ), задаваемая уравнением 3-й степени с коэффициентами из поля K{displaystyle K}
), задаваемая уравнением 3-й степени с коэффициентами из поля K{displaystyle K} и «точкой на бесконечности». В подходящих аффинных координатах её уравнение приводится к виду[1][2]:
и «точкой на бесконечности». В подходящих аффинных координатах её уравнение приводится к виду[1][2]:
- y2+a1xy+a3y=x3+a2x2+a4x+a6{displaystyle y^{2}+a_{1}xy+a_{3}y=x^{3}+a_{2}x^{2}+a_{4}x+a_{6}}
 .
.
Содержание
История
Древнейшим дошедшим до нашего времени источником, в котором рассматриваются кубические кривые, является «Арифметика» древнегреческого математика Диофанта. В этой работе ставится задача найти рациональные и нетривиальные решения уравнения y(6−y)=x3−x{displaystyle y(6-y)=x^{3}-x}
 . Диофант решает эту задачу при помощи подстановки x=3y−1{displaystyle x=3y-1}
. Диофант решает эту задачу при помощи подстановки x=3y−1{displaystyle x=3y-1} .
.
В 1670-х годах Ньютон, используя приемы аналитической геометрии, делает попытку классифицировать кубические кривые. В ходе исследований Ньютон заметил, что решение Диофанта состоит, по существу, в пересечении кривой, заданной уравнением y(6−y)=x3−x{displaystyle y(6-y)=x^{3}-x}
 с касательной x=3y−1{displaystyle x=3y-1}
с касательной x=3y−1{displaystyle x=3y-1} . Открытие Ньютона, в конечном итоге, привело к формулам сложения точек на эллиптической кривой. В XIX веке эллиптические кривые находят применениеa:not(:hover){border-bottom:1px dotted;text-decoration:none}}]]>[уточнить] в теории эллиптических функций, которые, в свою очередь, тесно связаны с эллиптическими интегралами. Таким образом, исторически термин «эллиптическая кривая» происходит от термина «эллиптический интеграл»[3].
. Открытие Ньютона, в конечном итоге, привело к формулам сложения точек на эллиптической кривой. В XIX веке эллиптические кривые находят применениеa:not(:hover){border-bottom:1px dotted;text-decoration:none}}]]>[уточнить] в теории эллиптических функций, которые, в свою очередь, тесно связаны с эллиптическими интегралами. Таким образом, исторически термин «эллиптическая кривая» происходит от термина «эллиптический интеграл»[3].
Каноническая форма
Если характеристика поля K{displaystyle K}
 (charK{displaystyle mathrm {char} ,K}
(charK{displaystyle mathrm {char} ,K} ) не равна 2 или 3, то уравнение с помощью замены координат приводится к канонической форме (форме Вейерштрасса):
) не равна 2 или 3, то уравнение с помощью замены координат приводится к канонической форме (форме Вейерштрасса):
- y2=x3+ax+b{displaystyle y^{2}=x^{3}+ax+b}
 .
.
Если charK=3{displaystyle mathrm {char} ,K=3}
 , то каноническим видом уравнения является вид:
, то каноническим видом уравнения является вид:
- y2=x3+a2x2+a4x+a6{displaystyle y^{2}=x^{3}+a_{2}x^{2}+a_{4}x+a_{6}}
 .
.
Если charK=2{displaystyle mathrm {char} ,K=2}
 , то уравнение приводится к одному из видов:
, то уравнение приводится к одному из видов:
- y2+y=x3+ax+b{displaystyle y^{2}+y=x^{3}+ax+b}
 — суперсингулярные кривые[en]
— суперсингулярные кривые[en]
или
- y2+xy=x3+ax2+b{displaystyle y^{2}+xy=x^{3}+ax^{2}+b}
 — несуперсингулярные кривые[4].
— несуперсингулярные кривые[4].
Эллиптические кривые над действительными числами
 Графики кривых y2 = x3 − x и y2 = x3 − x + 1
Графики кривых y2 = x3 − x и y2 = x3 − x + 1
Формальное определение эллиптической кривой требует некоторых знаний в алгебраической геометрии, но некоторые свойства эллиптических кривых над действительными числами можно описать, используя только знания алгебры и геометрии старших классов школы.
Поскольку характеристика поля действительных чисел — 0, а не 2 или 3, то эллиптическая кривая — плоская кривая, определяемая уравнением вида:
- y2=x3+ax+b{displaystyle y^{2}=x^{3}+ax+b}
 ,
,
где a{displaystyle a}
 и b{displaystyle b}
и b{displaystyle b} — действительные числа. Этот вид уравнений называется уравнениями Вейерштрасса.
— действительные числа. Этот вид уравнений называется уравнениями Вейерштрасса.
Определение эллиптической кривой также требует, чтобы кривая не имела особых точек. Геометрически это значит, что график не должен иметь каспов и самопересечений. Алгебраически, достаточно проверить, что дискриминант
- Δ=−16(4a3+27b2){displaystyle Delta =-16(4a^{3}+27b^{2})}
 [4]
[4]
не равен нулю.
Если кривая не имеет особых точек, то её график имеет две связные компоненты, если дискриминант положителен, и одну — если отрицателен. Например, для графиков выше в первом случае дискриминант равен 64, а во втором он равен −368.
Групповой закон
Добавлением «точки в бесконечности» получается проективный вариант этой кривой[5]. Если P{displaystyle P}
 и Q{displaystyle Q}
и Q{displaystyle Q} — две точки на кривой, то возможно единственным образом описать третью точку — точку пересечения данной кривой с прямой, проведённой через P{displaystyle P}
— две точки на кривой, то возможно единственным образом описать третью точку — точку пересечения данной кривой с прямой, проведённой через P{displaystyle P} и Q{displaystyle Q}
и Q{displaystyle Q} . Если прямая является касательной к кривой в точке, то такая точка считается дважды. Если прямая параллельна оси ординат, третьей точкой будет точка в бесконечности.
. Если прямая является касательной к кривой в точке, то такая точка считается дважды. Если прямая параллельна оси ординат, третьей точкой будет точка в бесконечности.
Таким образом, можно ввести групповую операцию «+» на кривой со следующими свойствами: точка в бесконечности (обозначаемая символом O{displaystyle O}
 ) является нейтральным элементом группы; и если прямая пересекает данную кривую в точках P{displaystyle P}
) является нейтральным элементом группы; и если прямая пересекает данную кривую в точках P{displaystyle P} , Q{displaystyle Q}
, Q{displaystyle Q} и R′{displaystyle R^{‘}}
и R′{displaystyle R^{‘}} , то P+Q+R′=O{displaystyle P+Q+R^{‘}=O}
, то P+Q+R′=O{displaystyle P+Q+R^{‘}=O} в группе. Суммой точек P{displaystyle P}
в группе. Суммой точек P{displaystyle P} и Q{displaystyle Q}
и Q{displaystyle Q} называется точка R=P+Q{displaystyle R=P+Q}
называется точка R=P+Q{displaystyle R=P+Q} , которая симметрична точке R′{displaystyle R^{‘}}
, которая симметрична точке R′{displaystyle R^{‘}} относительно оси Ox{displaystyle Ox}
относительно оси Ox{displaystyle Ox} . Можно показать, что относительно введённой таким образом операции лежащие на кривой точки и точка O{displaystyle O}
. Можно показать, что относительно введённой таким образом операции лежащие на кривой точки и точка O{displaystyle O} образуют абелеву группу; в частности, свойство ассоциативности операции «+» можно доказать, используя теорему о 9 точках на кубике[6].
образуют абелеву группу; в частности, свойство ассоциативности операции «+» можно доказать, используя теорему о 9 точках на кубике[6].
Данная группа может быть описана и алгебраически. Пусть дана кривая y2=x3+ax+b{displaystyle y^{2}=x^{3}+ax+b}
 над полем K{displaystyle K}
над полем K{displaystyle K} (характеристика которого не равна ни 2, ни 3), и точки P=(xP,yP){displaystyle P=(x_{P},y_{P})}
(характеристика которого не равна ни 2, ни 3), и точки P=(xP,yP){displaystyle P=(x_{P},y_{P})} и Q=(xQ,yQ){displaystyle Q=(x_{Q},y_{Q})}
и Q=(xQ,yQ){displaystyle Q=(x_{Q},y_{Q})} на кривой, допустим, что xP≠xQ{displaystyle x_{P}neq x_{Q}}
на кривой, допустим, что xP≠xQ{displaystyle x_{P}neq x_{Q}} . Пусть s=yP−yQxP−xQ{displaystyle textstyle s={frac {y_{P}-y_{Q}}{x_{P}-x_{Q}}}}
. Пусть s=yP−yQxP−xQ{displaystyle textstyle s={frac {y_{P}-y_{Q}}{x_{P}-x_{Q}}}} ; так как K — поле, то s строго определено. Тогда мы можем определить R=P+Q=(xR,yR){displaystyle R=P+Q=(x_{R},y_{R})}
; так как K — поле, то s строго определено. Тогда мы можем определить R=P+Q=(xR,yR){displaystyle R=P+Q=(x_{R},y_{R})} следующим образом:
следующим образом:
- xR=s2−xP−xQ{displaystyle x_{R}=s^{2}-x_{P}-x_{Q}}
 ,
,
- yR=−yP+s(xP−xR){displaystyle y_{R}=-y_{P}+s(x_{P}-x_{R})}
 .
.
Если xP=xQ{displaystyle x_{P}=x_{Q}}
 , то есть два варианта: если yP=−yQ{displaystyle y_{P}=-y_{Q}}
, то есть два варианта: если yP=−yQ{displaystyle y_{P}=-y_{Q}} , то сумма определена как 0; значит, обратную точку к любой точке на кривой можно найти, отразив её относительно оси Ox{displaystyle Ox}
, то сумма определена как 0; значит, обратную точку к любой точке на кривой можно найти, отразив её относительно оси Ox{displaystyle Ox} . Если yP=yQ≠0{displaystyle y_{P}=y_{Q}neq 0}
. Если yP=yQ≠0{displaystyle y_{P}=y_{Q}neq 0} , то R=P+P=2P=(xR,yR){displaystyle R=P+P=2P=(x_{R},y_{R})}
, то R=P+P=2P=(xR,yR){displaystyle R=P+P=2P=(x_{R},y_{R})} определяется так:
определяется так:
- s=3xP2+a2yP{displaystyle textstyle s={frac {3x_{P}^{2}+a}{2y_{P}}}}
 ,
,
- xR=s2−2xP{displaystyle x_{R}=s^{2}-2x_{P}}
 ,
,
- yR=−yP+s(xP−xR){displaystyle y_{R}=-y_{P}+s(x_{P}-x_{R})}
 .
.
Если yP=yQ=0{displaystyle y_{P}=y_{Q}=0}
 , то P+P=O{displaystyle P+P=O}
, то P+P=O{displaystyle P+P=O} .
.
Обратный элемент к точке P{displaystyle P}
 , обозначаемый −P{displaystyle -P}
, обозначаемый −P{displaystyle -P} и такой, что P+(−P)=0{displaystyle P+(-P)=0}
и такой, что P+(−P)=0{displaystyle P+(-P)=0} , в рассмотренной выше группе определятся так:
, в рассмотренной выше группе определятся так:
- Если координата yP{displaystyle y_{P}}
 точки P=(xP,yP){displaystyle P=(x_{P},y_{P})}
точки P=(xP,yP){displaystyle P=(x_{P},y_{P})} не равна 0{displaystyle 0}
не равна 0{displaystyle 0} , то −P=(xP,−yP){displaystyle -P=(x_{P},-y_{P})}
, то −P=(xP,−yP){displaystyle -P=(x_{P},-y_{P})} .
.
- Если yP=0{displaystyle y_{P}=0}
 , то −P=P=(xP,yP){displaystyle -P=P=(x_{P},y_{P})}
, то −P=P=(xP,yP){displaystyle -P=P=(x_{P},y_{P})} .
.
- Если P=O{displaystyle P=O}
 — точка на бесконечности, то и −P=O{displaystyle -P=O}
— точка на бесконечности, то и −P=O{displaystyle -P=O} [7].
[7].
Точка Q=nP{displaystyle Q=nP}
 , где n{displaystyle n}
, где n{displaystyle n} целое, определяется (при n>0{displaystyle n>0}
целое, определяется (при n>0{displaystyle n>0} ) как Q=P+P⋯+P⏟n{displaystyle Q=underbrace {P+Pdots +P} _{n}}
) как Q=P+P⋯+P⏟n{displaystyle Q=underbrace {P+Pdots +P} _{n}} . Если n<0{displaystyle n<0}
. Если n<0{displaystyle n<0} , то Q{displaystyle Q}
, то Q{displaystyle Q} есть обратный элемент к |n|P{displaystyle |n|P}
есть обратный элемент к |n|P{displaystyle |n|P} . Если n=0{displaystyle n=0}
. Если n=0{displaystyle n=0} , то Q=0⋅P=O{displaystyle Q=0cdot P=O}
, то Q=0⋅P=O{displaystyle Q=0cdot P=O} . Для примера покажем как найти точку Q=4P{displaystyle Q=4P}
. Для примера покажем как найти точку Q=4P{displaystyle Q=4P} : она представляется как 4P=2P+2P{displaystyle 4P=2P+2P}
: она представляется как 4P=2P+2P{displaystyle 4P=2P+2P} , а точка 2P{displaystyle 2P}
, а точка 2P{displaystyle 2P} находится по формуле 2P=P+P{displaystyle 2P=P+P}
находится по формуле 2P=P+P{displaystyle 2P=P+P} [8].
[8].
Эллиптические кривые над полем комплексных чисел
Формулировка эллиптических кривых как вложения тора в комплексную проективную плоскость естественным образом следует из свойства эллиптических функций Вейерштрасса, согласно которому они и их первые производные связаны формулой:
- ℘′(z)2=4℘(z)3−g2℘(z)−g3{displaystyle wp ‘(z)^{2}=4wp (z)^{3}-g_{2}wp (z)-g_{3}}
 ,
,
где g2{displaystyle g_{2}}
 и g3{displaystyle g_{3}}
и g3{displaystyle g_{3}} — константы; ℘(z){displaystyle wp (z)}
— константы; ℘(z){displaystyle wp (z)} — эллиптическая функция Вейерштрасса, а ℘′(z){displaystyle wp ‘(z)}
— эллиптическая функция Вейерштрасса, а ℘′(z){displaystyle wp ‘(z)} — её производная. Функции Вейерштрасса дважды периодичны, то есть периодичны относительно решётки[en]Λ{displaystyle Lambda }
— её производная. Функции Вейерштрасса дважды периодичны, то есть периодичны относительно решётки[en]Λ{displaystyle Lambda } , и следовательно определены на торе T=C/Λ{displaystyle T=mathbb {C} /Lambda }
, и следовательно определены на торе T=C/Λ{displaystyle T=mathbb {C} /Lambda } . Этот тор может быть вложен в комплексную проективную плоскость отображением:
. Этот тор может быть вложен в комплексную проективную плоскость отображением:
-
- z→(1,℘(z),℘′(z)){displaystyle zto (1,wp (z),wp ‘(z))}
 .
.
Это отображение — изоморфизм групп, позволяющий перенести естественную структуру группы тора на кривую в проективной плоскости. Кроме того, это изоморфизм римановых поверхностей, то есть топологически данную эллиптическую кривую можно рассматривать как тор. Если решётка Λ{displaystyle Lambda }
 связана с решёткой cΛ{displaystyle cLambda }
связана с решёткой cΛ{displaystyle cLambda } умножением на ненулевое комплексное число c{displaystyle c}
умножением на ненулевое комплексное число c{displaystyle c} , то соответствующие кривые изоморфны. Классы изоморфизма эллиптических кривых определены j-инвариантом[en].
, то соответствующие кривые изоморфны. Классы изоморфизма эллиптических кривых определены j-инвариантом[en].
Классы изоморфизма можно рассмотреть более простым образом. Константы g2{displaystyle g_{2}}
 и g3{displaystyle g_{3}}
и g3{displaystyle g_{3}} , называемые модулярными инвариантами, однозначно определяются решёткой, то есть структурой тора. С другой стороны, уравнение эллиптической кривой можно записать как
, называемые модулярными инвариантами, однозначно определяются решёткой, то есть структурой тора. С другой стороны, уравнение эллиптической кривой можно записать как
-
- y2=x(x−1)(x−λ){displaystyle y^{2}=x(x-1)(x-lambda )}
 .
.
Можно показать, что
-
- g2=41/33(λ2−λ+1){displaystyle g_{2}={frac {4^{1/3}}{3}}(lambda ^{2}-lambda +1)}

и
-
- g3=127(λ+1)(2λ2−5λ+2){displaystyle g_{3}={frac {1}{27}}(lambda +1)(2lambda ^{2}-5lambda +2)}
 ,
,
так что модулярный дискриминант[en] равен:
-
- Δ=g23−27g32=λ2(λ−1)2{displaystyle Delta =g_{2}^{3}-27g_{3}^{2}=lambda ^{2}(lambda -1)^{2}}
 .
.
Здесь λ{displaystyle lambda }
 иногда называют модулярной лямбда-функцией[en][9].
иногда называют модулярной лямбда-функцией[en][9].
Эллиптические кривые над полем рациональных чисел
Если коэффициенты уравнения эллиптической кривой E{displaystyle E}
 рациональны, то можно рассматривать множество рациональных точек на такой кривой (включая O{displaystyle O}
рациональны, то можно рассматривать множество рациональных точек на такой кривой (включая O{displaystyle O} ). Это множество образует подгруппу группы действительных точек (включая O{displaystyle O}
). Это множество образует подгруппу группы действительных точек (включая O{displaystyle O} ) на кривой E{displaystyle E}
) на кривой E{displaystyle E} с таким же групповым законом сложения точек на кривой. Это можно показать следующим образом: рассмотрим алгебраическую формулу получения координаты суммы двух точек P{displaystyle P}
с таким же групповым законом сложения точек на кривой. Это можно показать следующим образом: рассмотрим алгебраическую формулу получения координаты суммы двух точек P{displaystyle P} и Q{displaystyle Q}
и Q{displaystyle Q} , лежащих на кривой E{displaystyle E}
, лежащих на кривой E{displaystyle E} . Если эти точки и коэффициенты уравнения кривой рациональны, то координаты точки R=P+Q{displaystyle R=P+Q}
. Если эти точки и коэффициенты уравнения кривой рациональны, то координаты точки R=P+Q{displaystyle R=P+Q} тоже будут рациональны, так как xR{displaystyle x_{R}}
тоже будут рациональны, так как xR{displaystyle x_{R}} и yQ{displaystyle y_{Q}}
и yQ{displaystyle y_{Q}} являются рациональными функциями от коэффициентов кривой E{displaystyle E}
являются рациональными функциями от коэффициентов кривой E{displaystyle E} координат точек P{displaystyle P}
координат точек P{displaystyle P} и Q{displaystyle Q}
и Q{displaystyle Q} [10].
[10].
Порядком точки P{displaystyle P}
 на кривой E{displaystyle E}
на кривой E{displaystyle E} называется наименьшее натуральное k{displaystyle k}
называется наименьшее натуральное k{displaystyle k} такое, что kP=O{displaystyle kP=O}
такое, что kP=O{displaystyle kP=O} .
.
Для эллиптических кривых над полем рациональных чисел справедлива теорема Морделла[en]: на эллиптической кривой E{displaystyle E}
 существует такое конечное множество рациональных точек бесконечного порядка P1,P2,…,Pn{displaystyle P_{1},P_{2},dots ,P_{n}}
существует такое конечное множество рациональных точек бесконечного порядка P1,P2,…,Pn{displaystyle P_{1},P_{2},dots ,P_{n}} , что любая точка на эллиптической кривой представляется в виде:
, что любая точка на эллиптической кривой представляется в виде:
- P=a1P1+a2P2+…+anPn+Q{displaystyle P=a_{1}P_{1}+a_{2}P_{2}+…+a_{n}P_{n}+Q}
 ,
,
где a1,…,an{displaystyle a_{1},…,a_{n}}
 — целые числа, однозначно определенные для точки P{displaystyle P}
— целые числа, однозначно определенные для точки P{displaystyle P} , а Q{displaystyle Q}
, а Q{displaystyle Q} — точка кручения, являющаяся точкой конечного порядка.[11]. Другими словами, теорема гласит, что если поле K{displaystyle K}
— точка кручения, являющаяся точкой конечного порядка.[11]. Другими словами, теорема гласит, что если поле K{displaystyle K} — поле рациональных чисел, то группа K{displaystyle K}
— поле рациональных чисел, то группа K{displaystyle K} -рациональных точек — конечнопорождённая. Это означает, что группа может быть представлена как прямая сумма свободной абелевой группы и конечной подгруппы кручения[12].
-рациональных точек — конечнопорождённая. Это означает, что группа может быть представлена как прямая сумма свободной абелевой группы и конечной подгруппы кручения[12].
Рангом эллиптической кривой E{displaystyle E}
 называется минимальное число рациональных точек бесконечного порядка из теоремы Морделла. Нет общего алгоритма для вычисления ранга свободной подгруппы и, соответственно, ранга эллиптической кривой. Формула для вычисления ранга даётся в гипотезе Бёрча и Свиннертона-Дайера.На 2014 год эллиптическая кривая с максимальным точно известным рангом выглядит так:
называется минимальное число рациональных точек бесконечного порядка из теоремы Морделла. Нет общего алгоритма для вычисления ранга свободной подгруппы и, соответственно, ранга эллиптической кривой. Формула для вычисления ранга даётся в гипотезе Бёрча и Свиннертона-Дайера.На 2014 год эллиптическая кривая с максимальным точно известным рангом выглядит так:
- y2 + xy + y = x3 − x2 + 31368015812338065133318565292206590792820353345x + 302038802698566087335643188429543498624522041683
Её ранг равен 19, она была найдена Ноамом Элкисом[en]* в 2009 году[13]. Про следующую кривую, найденную Элкисом в 2006 году,
- y2 + xy + y = x3 − x2 + 20 067 762 415 575 527 000 000 000 000 000 000 000 000 000 000 000 000 000x + 34 481 611 795 030 556 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000 000
известно, что её ранг по крайне мере 28, однако точный ранг этой кривой неизвестен[14]. В 2016 году было опубликовано доказательство того, что ранг этой кривой равен в точности 28, если выполнена обобщённая гипотеза Римана[15].
Эллиптические кривые над конечными полями
Эллиптическую кривую E{displaystyle E}
 можно определить над конечным полем Fq{displaystyle mathbb {F} _{q}}
можно определить над конечным полем Fq{displaystyle mathbb {F} _{q}} , где q=pr{displaystyle q=p^{r}}
, где q=pr{displaystyle q=p^{r}} , а p{displaystyle p}
, а p{displaystyle p} простое.
простое.
Точное число точек эллиптической кривой E{displaystyle E}
 над конечным полем Fq{displaystyle mathbb {F} _{q}}
над конечным полем Fq{displaystyle mathbb {F} _{q}} достаточно трудно вычислить, но теорема Хассе об эллиптических кривых утверждает, что:
достаточно трудно вычислить, но теорема Хассе об эллиптических кривых утверждает, что:
- |♯E(Fq)−q−1|<2q{displaystyle left|sharp E(mathbb {F} _{q})-q-1right|<2{sqrt {q}}}
 [16].
[16].
Этот факт можно истолковать и доказать с помощью общей теории; см. Локальная дзета-функция?!, Этальные когомологии[en].
Число точек на конкретной кривой может быть вычислено с помощью алгоритма Шуфа?!.
Приложения
Эллиптические кривые над конечными полями используются в некоторых криптографических приложениях, для факторизации и тестирования простоты чисел. Обычно, основная идея, заложенная в этих приложениях, заключается в том, что известный алгоритм, используемый для конкретных конечных групп, переписывается для использования групп рациональных точек эллиптических кривых.
В теории чисел эллиптические кривые были, в частности, использованы Эндрю Уайлсом (совместно с Ричардом Тейлором) в доказательстве великой теоремы Ферма.
В криптографии они образуют самостоятельный раздел эллиптической криптографии, посвящённый изучению криптосистем на базе эллиптических кривых, в частности на эллиптических кривых основан российский стандарт ГОСТ Р 34.10-2001, описывающий алгоритмы формирования и проверки электронной цифровой подписи.
Примечания
- ↑ Silverman, 2009, p. 59.
- ↑ Коблиц, 2001, с. 188.
- ↑ Adrian Rice, Ezra Brown. Why Ellipses Are Not Elliptic Curves (англ.) // Mathematics Magazine. — 2012. — Vol. 85, no. 3. — P. 163—176.
- ↑ 1 2 Silverman, 2009, p. 42—43.
- ↑ Коблиц, 2001, с. 192.
- ↑ Острик, 2001, с. 21—24.
- ↑ Коблиц, 2001, с. 188—200.
- ↑ Острик, 2001, с. 24.
- ↑ Коблиц, 2000, с. 33—37.
- ↑ Silverman, 2009, p. 20.
- ↑ Острик, 2001, с. 26.
- ↑ Коблиц, 2001, с. 195.
- ↑ Dujella, Andrej. History of elliptic curves rank records (англ.). Andrej Dujella home page.
- ↑ Dujella, Andrej. «Construction of high rank elliptic curves and related Diophantine problems.» 7th Symposium on Algebra and Computation (AC 2007). 2007.
- ↑ Klagsbrun, Zev, Travis Sherman, and James Weigandt. «The Elkies curve has rank 28 subject only to GRH.» arXiv preprint arXiv:1606.07178 (2016).
- ↑ Silverman, 2009, p. 137—138.
Литература
- Клеменс, Г. Мозаика теории комплексных кривых. — М.: Мир, 1984.
- Коблиц Н. Курс теории чисел и криптографии = A Course in Number Theory and Cryptography. — М.: Научное изд-во «ТВП», 2001. — С. 188—200. — 254 с. — ISBN 5-85484-014-6.
- Острик В. В., Цфасман М. А. Алгебраическая геометрия и теория чисел: рациональные и эллиптические кривые. — М.: МЦНМО, 2001. — С. 48. — (Библиотека «Математическое просвещение»). — ISBN 5-900916-71-5.
- Коблиц Н. Введение в эллиптические кривые и модулярные формы = Introduction to Elliptic Curves and Modular Forms. — Новокузнецк: ИО НФМИ, 2000. — С. 33—37. — 312 с. — ISBN 5-8032-3325-0.
- Ленг С. Эллиптические функции = Elliptic functions. — Новокузнецк: ИО НФМИ, 2000. — С. 312. — ISBN 5-8032-3326-9.
- Joseph H. Silverman. The Arithmetic of Elliptic Curves. — N. Y.: Springer, 2009. — P. 42—43,59,137—138. — 408 p. — ISBN 978-0-387-09493-9.
Ссылки
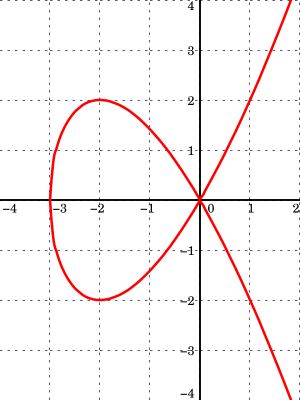 Куби́ка Чирнгауза — алгебраическая кривая третьего порядка.
Куби́ка Чирнгауза — алгебраическая кривая третьего порядка.
 принадлежит рассмотренной выше единичной окружности, однако не принадлежит её
принадлежит рассмотренной выше единичной окружности, однако не принадлежит её 



 .
.
 , где OP{displaystyle {mathcal {O}}_{P}}
, где OP{displaystyle {mathcal {O}}_{P}} —
—  — его
— его 
 —
—  (
( .
. . Диофант решает эту задачу при помощи подстановки x=3y−1{displaystyle x=3y-1}
. Диофант решает эту задачу при помощи подстановки x=3y−1{displaystyle x=3y-1} .
. ) не равна 2 или 3, то уравнение с помощью
) не равна 2 или 3, то уравнение с помощью  .
. , то каноническим видом уравнения является вид:
, то каноническим видом уравнения является вид: .
. , то уравнение приводится к одному из видов:
, то уравнение приводится к одному из видов: —
—  — несуперсингулярные кривые
— несуперсингулярные кривые
 и b{displaystyle b}
и b{displaystyle b} — действительные числа. Этот вид уравнений называется уравнениями Вейерштрасса.
— действительные числа. Этот вид уравнений называется уравнениями Вейерштрасса.
 и Q{displaystyle Q}
и Q{displaystyle Q} — две точки на кривой, то возможно единственным образом описать третью точку — точку пересечения данной кривой с прямой, проведённой через P{displaystyle P}
— две точки на кривой, то возможно единственным образом описать третью точку — точку пересечения данной кривой с прямой, проведённой через P{displaystyle P}
 ) является нейтральным элементом группы; и если прямая пересекает данную кривую в точках P{displaystyle P}
) является нейтральным элементом группы; и если прямая пересекает данную кривую в точках P{displaystyle P} , то P+Q+R′=O{displaystyle P+Q+R^{‘}=O}
, то P+Q+R′=O{displaystyle P+Q+R^{‘}=O} в группе. Суммой точек P{displaystyle P}
в группе. Суммой точек P{displaystyle P} , которая симметрична точке R′{displaystyle R^{‘}}
, которая симметрична точке R′{displaystyle R^{‘}} . Можно показать, что относительно введённой таким образом операции лежащие на кривой точки и точка O{displaystyle O}
. Можно показать, что относительно введённой таким образом операции лежащие на кривой точки и точка O{displaystyle O} и Q=(xQ,yQ){displaystyle Q=(x_{Q},y_{Q})}
и Q=(xQ,yQ){displaystyle Q=(x_{Q},y_{Q})} на кривой, допустим, что xP≠xQ{displaystyle x_{P}neq x_{Q}}
на кривой, допустим, что xP≠xQ{displaystyle x_{P}neq x_{Q}} . Пусть s=yP−yQxP−xQ{displaystyle textstyle s={frac {y_{P}-y_{Q}}{x_{P}-x_{Q}}}}
. Пусть s=yP−yQxP−xQ{displaystyle textstyle s={frac {y_{P}-y_{Q}}{x_{P}-x_{Q}}}} ; так как K — поле, то s строго определено. Тогда мы можем определить R=P+Q=(xR,yR){displaystyle R=P+Q=(x_{R},y_{R})}
; так как K — поле, то s строго определено. Тогда мы можем определить R=P+Q=(xR,yR){displaystyle R=P+Q=(x_{R},y_{R})} следующим образом:
следующим образом: ,
, .
. , то есть два варианта: если yP=−yQ{displaystyle y_{P}=-y_{Q}}
, то есть два варианта: если yP=−yQ{displaystyle y_{P}=-y_{Q}} , то сумма определена как 0; значит, обратную точку к любой точке на кривой можно найти, отразив её относительно оси Ox{displaystyle Ox}
, то сумма определена как 0; значит, обратную точку к любой точке на кривой можно найти, отразив её относительно оси Ox{displaystyle Ox} , то R=P+P=2P=(xR,yR){displaystyle R=P+P=2P=(x_{R},y_{R})}
, то R=P+P=2P=(xR,yR){displaystyle R=P+P=2P=(x_{R},y_{R})} определяется так:
определяется так: ,
, ,
, , то P+P=O{displaystyle P+P=O}
, то P+P=O{displaystyle P+P=O} .
. и такой, что P+(−P)=0{displaystyle P+(-P)=0}
и такой, что P+(−P)=0{displaystyle P+(-P)=0} , в рассмотренной выше группе определятся так:
, в рассмотренной выше группе определятся так: точки P=(xP,yP){displaystyle P=(x_{P},y_{P})}
точки P=(xP,yP){displaystyle P=(x_{P},y_{P})} , то −P=(xP,−yP){displaystyle -P=(x_{P},-y_{P})}
, то −P=(xP,−yP){displaystyle -P=(x_{P},-y_{P})} .
. , то −P=P=(xP,yP){displaystyle -P=P=(x_{P},y_{P})}
, то −P=P=(xP,yP){displaystyle -P=P=(x_{P},y_{P})} .
. — точка на бесконечности, то и −P=O{displaystyle -P=O}
— точка на бесконечности, то и −P=O{displaystyle -P=O}
 , где n{displaystyle n}
, где n{displaystyle n} целое, определяется (при n>0{displaystyle n>0}
целое, определяется (при n>0{displaystyle n>0} ) как Q=P+P⋯+P⏟n{displaystyle Q=underbrace {P+Pdots +P} _{n}}
) как Q=P+P⋯+P⏟n{displaystyle Q=underbrace {P+Pdots +P} _{n}} . Если n<0{displaystyle n<0}
. Если n<0{displaystyle n<0} , то Q{displaystyle Q}
, то Q{displaystyle Q} . Если n=0{displaystyle n=0}
. Если n=0{displaystyle n=0} , то Q=0⋅P=O{displaystyle Q=0cdot P=O}
, то Q=0⋅P=O{displaystyle Q=0cdot P=O} . Для примера покажем как найти точку Q=4P{displaystyle Q=4P}
. Для примера покажем как найти точку Q=4P{displaystyle Q=4P} : она представляется как 4P=2P+2P{displaystyle 4P=2P+2P}
: она представляется как 4P=2P+2P{displaystyle 4P=2P+2P} , а точка 2P{displaystyle 2P}
, а точка 2P{displaystyle 2P} находится по формуле 2P=P+P{displaystyle 2P=P+P}
находится по формуле 2P=P+P{displaystyle 2P=P+P}
 ,
, и g3{displaystyle g_{3}}
и g3{displaystyle g_{3}} — константы; ℘(z){displaystyle wp (z)}
— константы; ℘(z){displaystyle wp (z)} —
—  — её производная. Функции Вейерштрасса дважды периодичны, то есть периодичны относительно
— её производная. Функции Вейерштрасса дважды периодичны, то есть периодичны относительно  , и следовательно определены на торе T=C/Λ{displaystyle T=mathbb {C} /Lambda }
, и следовательно определены на торе T=C/Λ{displaystyle T=mathbb {C} /Lambda } . Этот тор может быть вложен в комплексную проективную плоскость отображением:
. Этот тор может быть вложен в комплексную проективную плоскость отображением: .
. умножением на ненулевое комплексное число c{displaystyle c}
умножением на ненулевое комплексное число c{displaystyle c} , то соответствующие кривые изоморфны. Классы изоморфизма эллиптических кривых определены
, то соответствующие кривые изоморфны. Классы изоморфизма эллиптических кривых определены  .
.
 ,
, .
. иногда называют
иногда называют  рациональны, то можно рассматривать множество рациональных точек на такой кривой (включая O{displaystyle O}
рациональны, то можно рассматривать множество рациональных точек на такой кривой (включая O{displaystyle O} и yQ{displaystyle y_{Q}}
и yQ{displaystyle y_{Q}} являются
являются  такое, что kP=O{displaystyle kP=O}
такое, что kP=O{displaystyle kP=O} .
. , что любая точка на эллиптической кривой представляется в виде:
, что любая точка на эллиптической кривой представляется в виде: ,
, — целые числа, однозначно определенные для точки P{displaystyle P}
— целые числа, однозначно определенные для точки P{displaystyle P} , где q=pr{displaystyle q=p^{r}}
, где q=pr{displaystyle q=p^{r}} , а p{displaystyle p}
, а p{displaystyle p} простое.
простое.
