Усечё́нная пирами́да — многогранник, образованный пирамидой и её сечением, параллельным основанию.[1].
Содержание
Произвольная усечённая пирамида
Формулы для усечённой пирамиды
Объём пирамиды V=13h(S1+S1S2+S2){displaystyle V={frac {1}{3}}h(S_{1}+{sqrt {S_{1}S_{2}}}+S_{2})}
, где S1,S2{displaystyle S_{1},S_{2}} — площади оснований, h{displaystyle h} — высота усечённой пирамиды.
Площадь боковой поверхности Sb=∑i=1nSi{displaystyle S_{b}=sum _{i=1}^{n}S_{i}}
равна сумме площадей боковых граней усечённой пирамиды.
Правильная усечённая пирамида
Определение
Правильная усечённая пирамида — многогранник, образованный правильной пирамидой и её сечением, параллельным основанию.
Формулы
- Sb=12(p1+p2)l{displaystyle S_{b}={frac {1}{2}}(p_{1}+p_{2})l} (Площадь боковой поверхности правильной усечённой пирамиды равна полупроизведению суммы периметров её оснований и апофемы)
- Sb=|S1−S2|cosφ{displaystyle S_{b}={frac {|S_{1}-S_{2}|}{cos varphi }}} , где S1,S2{displaystyle S_{1},S_{2}}
— площади оснований, а φ{displaystyle varphi } — двугранный угол при основании пирамиды.
См. также
Примечания
| Это заготовка статьи по геометрии. Вы можете помочь проекту, дополнив её. |
http://www-formula.ru/index.php/2011-09-24-00-29-48
| В статье не хватает ссылок на источники (см. также рекомендации по поиску).Информация должна быть проверяема, иначе она может быть удалена. Вы можете отредактировать статью, добавив ссылки на авторитетные источники в виде сносок. Эта отметка установлена 15 мая 2011 года. |


 , где S1,S2{displaystyle S_{1},S_{2}}
, где S1,S2{displaystyle S_{1},S_{2}} — высота усечённой пирамиды.
— высота усечённой пирамиды. равна сумме площадей боковых граней усечённой пирамиды.
равна сумме площадей боковых граней усечённой пирамиды.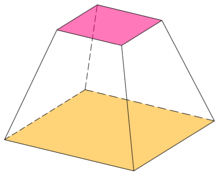
 (Площадь боковой поверхности правильной усечённой пирамиды равна полупроизведению суммы периметров её оснований и апофемы)
(Площадь боковой поверхности правильной усечённой пирамиды равна полупроизведению суммы периметров её оснований и апофемы) , где S1,S2{displaystyle S_{1},S_{2}}
, где S1,S2{displaystyle S_{1},S_{2}} —
— 