Парабола

Разделы:

У этого термина существуют и другие значения, см. Парабола (значения).

Пара́бола (греч. παραβολή — приложение) — геометрическое место точек, равноудалённых от данной прямой (называемой директрисой параболы) и данной точки (называемой фокусом параболы).

Парабола
Парабола, её фокус и директриса
Парабола как коническое сечение
Эксцентриситет	e=1{displaystyle textstyle e=1} ${displaystyle textstyle e=1}$
Уравнения
y=x2y=ax2+bx+cAx2+Bxy+Cy2+Dx+Ey=F(B2−4AC=0){displaystyle {begin{smallmatrix}y=x^{2}\[10pt]y=ax^{2}+bx+c\[10pt]Ax^{2}+Bxy+Cy^{2}+Dx+Ey=F\(B^{2}-4AC=0)end{smallmatrix}}} $begin{smallmatrix} y=x^2\[10pt] y=ax^2+bx+c\[10pt] Ax^2+Bxy+Cy^2+Dx+Ey=F \ (B^2-4AC=0) end{smallmatrix}$
Другие конические сечения
Гипербола Парабола Эллипс Окружность

Наряду с эллипсом и гиперболой, парабола является коническим сечением. Она может быть определена как коническое сечение с единичным эксцентриситетом.

Изображение конического сечения, являющегося параболой Построение параболы как конического сечения Конические сечения

Содержание

1 Вершина
2 Уравнения
3 Свойства
4 Связанные определения
5 Обобщение
6 Параболы в физическом пространстве
7 См. также
8 Примечания
9 Литература
10 Ссылки

Вершина

Точка параболы, ближайшая к её директрисе, называется вершиной этой параболы. Вершина является серединой перпендикуляра, опущенного из фокуса на директрису.

Уравнения

Каноническое уравнение параболы в прямоугольной системе координат:

y2=2px,p>0{displaystyle textstyle y^{2}=2px,p>0}

{displ aystyle textstyle y^{2}=2px,p>0}

(или x2=2py{displaystyle textstyle x^{2}=2py}

{displaystyle textstyle x^{2}=2py}

, если поменять местами оси).

Число p называется фокальным параметром, оно равно расстоянию от фокуса до директрисы[1]. Поскольку каждая точка параболы равноудалена от фокуса и директрисы, то и вершина — тоже, поэтому она лежит между фокусом и директрисой на расстоянии p2{displaystyle {frac {p}{2}}}

$frac{p}{2}$ от обоих.

Вывод
Уравнение директрисы PQ: x+p2=0{displaystyle textstyle x+{frac {p}{2}}=0} ${displaystyle textstyle x+{frac {p}{2}}=0}$ , фокус F имеет координаты (p2;0).{displaystyle left({frac {p}{2}};0right).} $left (frac{p}{2};0right ).$ Таким образом, начало координат O — середина отрезка CF. По определению параболы, для любой точки M, лежащей на ней, выполняется равенство KM = FM. Далее, поскольку KM=KD+DM=p2+x{displaystyle {textrm {KM=KD+DM}}={frac {p}{2}}+x} $textrm{KM=KD+DM}=frac{p}{2}+x$ и FM=(x−p2)2+y2{displaystyle {textrm {FM}}={sqrt {left(x-{frac {p}{2}}right)^{2}+y^{2}}}} $textrm{FM}=sqrt{left (x-frac{p}{2}right )^2+y^2}$ , то равенство приобретает вид: (x−p2)2+y2=p2+x.{displaystyle {sqrt {left(x-{frac {p}{2}}right)^{2}+y^{2}}}={frac {p}{2}}+x.} ${displaystyle {sqrt {left(x-{frac {p}{2}}right)^{2}+y^{2}}}={frac {p}{2}}+x.}$ После возведения в квадрат и некоторых преобразований получается равносильное уравнение y2=2px.{displaystyle y^{2}=2px.} ${displaystyle y^{2}=2px.}$

Вывод

Уравнение директрисы PQ: x+p2=0{displaystyle textstyle x+{frac {p}{2}}=0}

${displaystyle textstyle x+{frac {p}{2}}=0}$ , фокус F имеет координаты (p2;0).{displaystyle left({frac {p}{2}};0right).} $left (frac{p}{2};0right ).$ Таким образом, начало координат O — середина отрезка CF. По определению параболы, для любой точки M, лежащей на ней, выполняется равенство KM = FM. Далее, поскольку KM=KD+DM=p2+x{displaystyle {textrm {KM=KD+DM}}={frac {p}{2}}+x} $textrm{KM=KD+DM}=frac{p}{2}+x$ и FM=(x−p2)2+y2{displaystyle {textrm {FM}}={sqrt {left(x-{frac {p}{2}}right)^{2}+y^{2}}}} $textrm{FM}=sqrt{left (x-frac{p}{2}right )^2+y^2}$ , то равенство приобретает вид:

(x−p2)2+y2=p2+x.{displaystyle {sqrt {left(x-{frac {p}{2}}right)^{2}+y^{2}}}={frac {p}{2}}+x.}

{displaystyle {sqrt {left(x-{frac {p}{2}}right)^{2}+y^{2}}}={frac {p}{2}}+x.}

После возведения в квадрат и некоторых преобразований получается равносильное уравнение y2=2px.{displaystyle y^{2}=2px.}

${displaystyle y^{2}=2px.}$

Парабола, заданная квадратичной функцией

Квадратичная функция y=ax2+bx+c{displaystyle y=ax^{2}+bx+c}

$y=ax^{2}+bx+c$ при a≠0{displaystyle aneq 0} $aneq 0$ также является уравнением параболы и графически изображается той же параболой, что и y=ax2,{displaystyle y=ax^{2},} ${displaystyle y=ax^{2},}$ но в отличие от последней имеет вершину не в начале координат, а в некоторой точке A, координаты которой вычисляются по формулам:

xA=−b2a,yA=−D4a,{displaystyle x_{textrm {A}}=-{frac {b}{2a}},;y_{textrm {A}}=-{frac {D}{4a}},}

{displaystyle x_{textrm {A}}=-{frac {b}{2a}},;y_{textrm {A}}=-{frac {D}{4a}},}

где D=b2−4ac{displaystyle D=b^{2}-4ac}

D=b^2-4ac

— дискриминант квадратного трёхчлена.

Ось симметрии параболы, заданной квадратичной функцией, проходит через вершину параллельно оси ординат. При a > 0 (a < 0) фокус лежит на этой оси над (под) вершиной на расстоянии 1/4a, а директриса — под (над) вершиной на таком же расстоянии и параллельна оси абсцисс. Уравнение y=ax2+bx+c{displaystyle y=ax^{2}+bx+c}

$y=ax^{2}+bx+c$ может быть представлено в виде y=a(x−xA)2+yA,{displaystyle y=a(x-x_{textrm {A}})^{2}+y_{textrm {A}},} ${displaystyle y=a(x-x_{textrm {A}})^{2}+y_{textrm {A}},}$ а в случае переноса начала координат в точку A уравнение параболы превращается в каноническое. Таким образом, для каждой квадратичной функции можно найти систему координат такую, что в этой системе уравнение соответствующей параболы представляется каноническим. При этом p=1|2a|.{displaystyle p={frac {1}{|2a|}}.} $p=frac{1}{|2a|}.$

Общее уравнение параболы

В общем случае парабола не обязана иметь ось симметрии, параллельную одной из координатных осей. Однако, как и любое другое коническое сечение, парабола является кривой второго порядка и, следовательно, её уравнение на плоскости в декартовой системе координат может быть записано в виде квадратного многочлена:

Ax2+Bxy+Cy2+Dx+Ey+F=0.{displaystyle Ax^{2}+Bxy+Cy^{2}+Dx+Ey+F=0.}

Ax^2+Bxy+Cy^2+Dx+Ey+F=0.

Если кривая второго порядка, заданная в таком виде, является параболой, то составленный из коэффициентов при старших членах дискриминант B2−4AC{displaystyle B^{2}-4AC}

$B^2-4AC$ равен нулю.

Уравнение в полярной системе

Парабола в полярной системе координат (ρ,ϑ){displaystyle (rho ,vartheta )}

$(rho,vartheta)$ с центром в фокусе и нулевым направлением вдоль оси параболы (от фокуса к вершине) может быть представлена уравнением

ρ(1+cos⁡ϑ)=p,{displaystyle rho (1+cos vartheta )=p,}

rho (1 + cos vartheta) = p,

где p — фокальный параметр (расстояние от фокуса до директрисы или удвоенное расстояние от фокуса до вершины)

Расчёт коэффициентов квадратичной функции

Если для уравнения параболы с осью, параллельной оси ординат, y=ax2+bx+c{displaystyle y=ax^{2}+bx+c}

${displaystyle y=ax^{2}+bx+c}$ известны координаты трёх различных точек параболы (x1;y1),(x2;y2),(x3;y3),{displaystyle (x_{1};y_{1}),;(x_{2};y_{2}),;(x_{3};y_{3}),} ${displaystyle (x_{1};y_{1}),;(x_{2};y_{2}),;(x_{3};y_{3}),}$ то его коэффициенты могут быть найдены так:

a=y3−x3(y2−y1)+x2y1−x1y2x2−x1x3(x3−x1−x2)+x1x2, b=y2−y1x2−x1−a(x1+x2), c=x2y1−x1y2x2−x1+ax1x2.{displaystyle a={frac {y_{3}-{tfrac {x_{3}(y_{2}-y_{1})+x_{2}y_{1}-x_{1}y_{2}}{x_{2}-x_{1}}}}{x_{3}(x_{3}-x_{1}-x_{2})+x_{1}x_{2}}}, b={frac {y_{2}-y_{1}}{x_{2}-x_{1}}}-a(x_{1}+x_{2}), c={frac {x_{2}y_{1}-x_{1}y_{2}}{x_{2}-x_{1}}}+ax_{1}x_{2}.}

a=frac{y_{3}-tfrac{x_{3}(y_{2}-y_{1})+x_{2}y_{1}-x_{1}y_{2}}{x_{2}-x_{1}}}{x_{3}(x_{3}-x_{1}-x_{2})+x_{1}x_{2}}, b=frac{y_{2}-y_{1}}{x_{2}-x_{1}}-a(x_{1}+x_{2}), c=frac{x_{2}y_{1}-x_{1}y_{2}}{x_{2}-x_{1}}+ax_{1}x_{2}.

Если же заданы вершина (x0;y0){displaystyle (x_{0};y_{0})}

$(x_{0};y_{0})$ и старший коэффициент a{displaystyle a} $a$ , то остальные коэффициенты и корни вычисляются по формулам:

b=−2ax0{displaystyle b=-2ax_{0}}

b=-2ax_0

c=ax02+y0{displaystyle c=ax_{0}^{2}+y_{0}}

c=ax_0^2+y_0

x1=x0+−y0a{displaystyle x_{1}=x_{0}+{sqrt {-{frac {y_{0}}{a}}}}}

x2=x0−−y0a{displaystyle x_{2}=x_{0}-{sqrt {-{frac {y_{0}}{a}}}}}

x_2=x_0-sqrt{-frac{y_0}{a}}

Свойства

Отражательное свойство параболы (оптика) Расстояние от Pn до фокуса F такое же, как и от Pn до Qn (на директрисе L) Длина линий FPnQn одинакова. Можно сказать, что, в отличие от эллипса, второй фокус у параболы — в бесконечности (см. также Шары Данделена)

Парабола — кривая второго порядка.
Она имеет ось симметрии, называемой осью параболы. Ось проходит через фокус и вершину перпендикулярно директрисе.
Оптическое свойство. Пучок лучей, параллельных оси параболы, отражаясь в параболе, собирается в её фокусе. И наоборот, свет от источника, находящегося в фокусе, отражается параболой в пучок параллельных её оси лучей.
Если фокус параболы отразить относительно касательной, то его образ будет лежать на директрисе.
Отрезок, соединяющий середину произвольной хорды параболы и точку пересечения касательных к ней в концах этой хорды, перпендикулярен директрисе, а его середина лежит на параболе.
Парабола является антиподерой прямой.
Все параболы подобны. Расстояние между фокусом и директрисой определяет масштаб.
Траектория фокуса параболы, катящейся по прямой, есть Цепная линия [2].

Связанные определения

При вращении параболы вокруг оси симметрии получается эллиптический параболоид.

Обобщение

Парабола есть Синусоидальная спираль при n=−12{displaystyle textstyle n=-{frac {1}{2}}}

$textstyle n=-{frac {1}{2}}$ ;

Параболы в физическом пространстве

Параболический компас Леонардо да Винчи

Траектории некоторых космических тел (комет, астероидов и других), проходящих вблизи звезды или другого массивного объекта (звезды или планеты) на достаточно большой скорости, имеют форму параболы (или гиперболы). Эти тела, вследствие своей большой скорости, не захватываются гравитационным полем звезды и продолжают свободный полёт. Это явление используется для гравитационных манёвров космических кораблей (в частности, аппаратов Вояджер).

Для создания невесомости в земных условиях проводятся полёты самолётов по параболической траектории, так называемой параболе Кеплера.

При отсутствии сопротивления воздуха траектория полёта тела в приближении однородного гравитационного поля представляет собой параболу.

Также параболические зеркала используются в любительских переносных телескопах систем Кассергена, Шмидта — Кассергена, Ньютона, а в фокусе параболы устанавливают вспомогательные зеркала, подающие изображение на окуляр.

При вращении сосуда с жидкостью вокруг вертикальной оси поверхность жидкости в сосуде и вертикальная плоскость пересекаются по параболе.

Свойство параболы фокусировать пучок лучей, параллельных оси параболы, используется в конструкциях прожекторов, фонарей, фар, а также телескопов-рефлекторов (оптических, инфракрасных, радио- …), в конструкции узконаправленных (спутниковых и других) антенн, необходимых для передачи данных на большие расстояния, солнечных электростанций и в других областях.

Форма параболы иногда используется в архитектуре для строительства крыш и куполов.

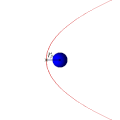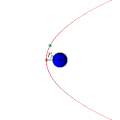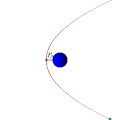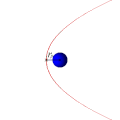
Параболическая орбита и движение спутника по ней (анимация)
Падение баскетбольного мяча
Параболическая солнечная электростанция в Калифорнии, США
Параболические траектории струй воды
Вращающийся сосуд с жидкостью
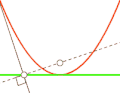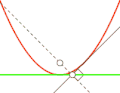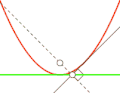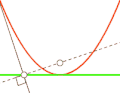
Парабола — антиподера прямой

См. также

Квадратичная функция
Кривая второго порядка
Кубическая парабола
Конические сечения:
Парабола Ладовского
Параболы, вписанные в треугольник (в том числе парабола Киперта)
Полукубическая парабола (парабола Нейла)
Параболоид
Шары Данделена
Цепная линия
Каустика

Примечания

↑ Александров П.С. Парабола // Курс аналитической геометрии и линейной алгебры. — М.: Наука, 1979. — С. 69—72. — 512 с.
↑ Савелов А. А. Плоские кривые. Систематика, свойства, применения (Справочное руководство)/ Под ред. А. П. Нордена. М.: Физматлит, 1960. С. 250.

Литература

Бронштейн И. Парабола // Квант. — 1975. — № 4. — С. 9—16.
Математическая энциклопедия (в 5-и томах). — М.: Советская Энциклопедия, 1982.
Маркушевич А. И. Замечательные кривые. — Гостехиздат, 1952. — 32 с. — (Популярные лекции по математике, выпуск 4).
А. А. Акопян, А. В. Заславский. Геометрические свойства кривых второго порядка. — М.: МЦНМО, 2007. — 136 с.

Ссылки

В Викисловаре есть статья «парабола»

Медиафайлы на Викискладе

Статья в справочнике «Прикладная математика».
Анимированные рисунки, иллюстрирующие некоторые свойства параболы.
Информация (англ.) о связи параболы с физикой.
Учебный фильм о параболе