Касательная прямая

• Пусть функция ${\displaystyle f\colon U(x_{0})\subset \mathbb {R} \to \mathbb {R} }$  определена в некоторой окрестности точки ${\displaystyle x_{0}\in \mathbb {R} }$ , и дифференцируема в ней: ${\displaystyle f\in {\mathcal {D}}(x_{0})}$ . Касательной прямой к графику функции ${\displaystyle f}$  в точке ${\displaystyle x_{0}}$  называется график линейной функции, задаваемой уравнением

  ${\displaystyle y=f(x_{0})+f'(x_{0})(x-x_{0}),\quad x\in \mathbb {R} .}$ 

• Если функция ${\displaystyle f}$  имеет в точке ${\displaystyle x_{0}}$  бесконечную производную ${\displaystyle f'(x_{0})=\pm \infty ,}$  то касательной прямой в этой точке называется вертикальная прямая, задаваемая уравнением

  ${\displaystyle x=x_{0}.}$ 

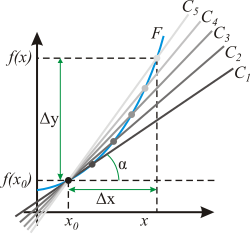
Прямо из определения следует, что график касательной прямой проходит через точку ${\displaystyle (x_{0},f(x_{0}))}$ . Угол ${\displaystyle \alpha }$  между касательной к кривой и осью Ох удовлетворяет уравнению

${\displaystyle \operatorname {tg} \,\alpha =f'(x_{0})=k,}$ 

где ${\displaystyle \operatorname {tg} }$  обозначает тангенс, а ${\displaystyle \operatorname {k} }$  — коэффициент наклона касательной. Производная в точке ${\displaystyle x_{0}}$  равна угловому коэффициенту касательной к графику функции y = f(x) в этой точке.

Пусть ${\displaystyle f\colon U(x_{0})\to \mathbb {R} }$  и ${\displaystyle x_{1}\in U(x_{0}).}$  Тогда прямая линия, проходящая через точки ${\displaystyle (x_{0},f(x_{0}))}$  и ${\displaystyle (x_{1},f(x_{1}))}$  задаётся уравнением

${\displaystyle y=f(x_{0})+{\frac {f(x_{1})-f(x_{0})}{x_{1}-x_{0}}}(x-x_{0}).}$ 

Эта прямая проходит через точку ${\displaystyle (x_{0},f(x_{0}))}$  для любого ${\displaystyle x_{1}\in U(x_{0}),}$  и её угол наклона ${\displaystyle \alpha (x_{1})}$  удовлетворяет уравнению

${\displaystyle \operatorname {tg} \,\alpha (x_{1})={\frac {f(x_{1})-f(x_{0})}{x_{1}-x_{0}}}.}$ 

В силу существования производной функции ${\displaystyle f}$  в точке ${\displaystyle x_{0},}$  переходя к пределу при ${\displaystyle x_{1}\to x_{0},}$  получаем, что существует предел

${\displaystyle \lim \limits _{x_{1}\to x_{0}}\operatorname {tg} \,\alpha (x_{1})=f'(x_{0}),}$ 

а в силу непрерывности арктангенса и предельный угол

${\displaystyle \alpha =\operatorname {arctg} \,f'(x_{0}).}$ 

Прямая, проходящая через точку ${\displaystyle (x_{0},f(x_{0}))}$  и имеющая предельный угол наклона, удовлетворяющий ${\displaystyle \operatorname {tg} \,\alpha =f'(x_{0}),}$  задаётся уравнением касательной:

${\displaystyle y=f(x_{0})+f'(x_{0})(x-x_{0}).}$ 

Прямая, имеющая одну общую точку с окружностью и лежащая с ней в одной плоскости, называется касательной к окружности.

Свойства

1. Касательная к окружности перпендикулярна к радиусу, проведённому в точку касания.
2. Отрезки касательных к окружности, проведённые из одной точки, равны и составляют равные углы с прямой, проходящей через эту точку и центр окружности.
3. Длина отрезка касательной, проведённой к окружности единичного радиуса, взятого между точкой касания и точкой пересечения касательной с радиусом, является тангенсом угла между этим радиусом и направлением от центра окружности на точку касания. «Тангенс» от лат. tangens — «касательная».

Односторонние полукасательные

• Если существует правая производная ${\displaystyle f'_{+}(x_{0})<\infty ,}$  то пра́вой полукаса́тельной к графику функции ${\displaystyle f}$  в точке ${\displaystyle x_{0}}$  называется луч

${\displaystyle y=f(x_{0})+f'_{+}(x_{0})(x-x_{0}),\quad x\geqslant x_{0}.}$ 

• Если существует левая производная ${\displaystyle f'_{-}(x_{0})<\infty ,}$  то ле́вой полукаса́тельной к графику функции ${\displaystyle f}$  в точке ${\displaystyle x_{0}}$  называется луч

${\displaystyle y=f(x_{0})+f'_{-}(x_{0})(x-x_{0}),\quad x\leqslant x_{0}.}$ 

• Если существует бесконечная правая производная ${\displaystyle f'_{+}(x_{0})=+\infty \;(-\infty ),}$  то правой полукасательной к графику функции ${\displaystyle f}$  в точке ${\displaystyle x_{0}}$  называется луч

${\displaystyle x=x_{0},\;y\geqslant f(x_{0})\;(y\leqslant f(x_{0})).}$ 

• Если существует бесконечная левая производная ${\displaystyle f'_{-}(x_{0})=+\infty \;(-\infty ),}$  то правой полукасательной к графику функции ${\displaystyle f}$  в точке ${\displaystyle x_{0}}$  называется луч

${\displaystyle x=x_{0},\;y\leqslant f(x_{0})\;(y\geqslant f(x_{0})).}$ 

• Дифференцируемая функция
• Касательное пространство
• Нормаль, бинормаль
• Теорема о секущих