У этого термина существуют и другие значения, см. Гиперболоид (значения).
Гиперболоид (от др.-греч. ὑπερβολή — гипербола, и εἶδος — вид, внешность). В математике гиперболоид — это вид поверхности второго порядка в трёхмерном пространстве, задаваемый в декартовых координатах уравнением
 Однополостный гиперболоид
Однополостный гиперболоид Двуполостный гиперболоид
Двуполостный гиперболоид
- x2a2+y2b2−z2c2=1{displaystyle {x^{2} over a^{2}}+{y^{2} over b^{2}}-{z^{2} over c^{2}}=1} (однополостный гиперболоид),
где a и b — действительные полуоси, а c — мнимая полуось;
или
- −x2a2−y2b2+z2c2=1{displaystyle -{x^{2} over a^{2}}-{y^{2} over b^{2}}+{z^{2} over c^{2}}=1} (двуполостный гиперболоид),
где a и b — мнимые полуоси, а c — действительная полуось.
Если a = b, то такая поверхность называется гиперболоидом вращения. Однополостный гиперболоид вращения может быть получен вращением гиперболы вокруг её мнимой оси, двухполостный — вокруг действительной. Двухполостный гиперболоид вращения также является геометрическим местом точек P, модуль разности расстояний от которых до двух заданных точек A и B постоянен: |AP−BP|=const{displaystyle |AP-BP|=const}. В этом случае A и B называются фокусами гиперболоида.
Однополостный гиперболоид является дважды линейчатой поверхностью; если он является гиперболоидом вращения, то он может быть получен вращением прямой вокруг другой прямой, скрещивающейся с ней.
Содержание
В науке и технике
 Оптическая схема телескопа Кассегрена. Малое зеркало имеет форму гиперболоида.
Оптическая схема телескопа Кассегрена. Малое зеркало имеет форму гиперболоида.
Свойство двуполостного гиперболоида вращения отражать лучи, направленные в один из фокусов, в другой фокус, используется в телескопах системы Кассегрена и в антеннах Кассегрена.
В искусстве
В архитектуре
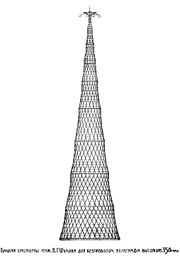 Проект 350-метровой башни В. Г. Шухова, 1919Основная статья: Гиперболоидные конструкции
Проект 350-метровой башни В. Г. Шухова, 1919Основная статья: Гиперболоидные конструкции
Линейчатая конструкция, имеющая форму однополостного гиперболоида, является жёсткой: если балки соединить шарнирно, гиперболоидная конструкция всё равно будет сохранять свою форму под действием внешних сил.
Для высоких сооружений основную опасность несёт ветровая нагрузка, а у решётчатой конструкции она невелика. Эти особенности делают гиперболоидные конструкции прочными, несмотря на невысокую материалоёмкость.
Примерами гиперболоидных конструкций являются:
- Шуховская башня
- Шуховская башня на Оке
- Аджигольский маяк
- Гиперболоидные мачты броненосца «Император Павел I»
- Гиперболоидные мачты американского линкора «Аризона»
- Башня порта Кобе
- Телебашня Гуанчжоу
- Aspire Tower
- Сиднейская телебашня
- Проект «Вортекс»
- Проект «Хрустальный остров»
В литературе
- Гиперболоид инженера Гарина (хотя на самом деле это должен был быть параболоид)
См. также
- Теорема о прямолинейных образующих однополосного гиперболоида
- Параболоид — другой вид поверхности второго порядка
- Гиперболический параболоид
- Гиперболоидные конструкции

 (однополостный гиперболоид),
(однополостный гиперболоид), (двуполостный гиперболоид),
(двуполостный гиперболоид), . В этом случае A и B называются
. В этом случае A и B называются 